3.5.3. Физическое моделирование структуры потоков Сокращение исчерпывающего описания для объекта-оригинала. Уравнения Навье - Стокса:

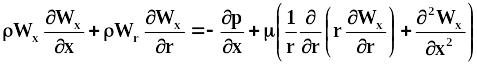, (3.34)

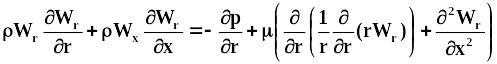. (3.35)

Система уравнений дополняется уравнением неразрывности :

. (3.36)

Выбор оптимальной физической модели. Для подобия модели оригиналу необходимо соблюдение подобия условий однозначности, включающих в себя для рассматриваемого примера геометрическое подобие, подобие физических величин и граничных условий, т.е. модель должна иметь те же пропорции, что и оригинал L/d=idem, d₀/d=idem. Кроме того, необходимо подобие поля скоростей во входящих потоках. Равенство скоростей нулю на границе с твердой стенкой будет обеспечиваться автоматически.

3.5.4. Сопряженное физическое и математическое моделирование

структуры потоков .

Выделение характерных зон аппарата. Анализ поведения турбулентного потока в аппарате (см. рис. 3.2) позволяет выделить 8 характерных зон [6]: 1, 7 - застойные зоны; 2, 6 - зоны смешения; 3 - пограничный слой; 4, 5, 8 - ядро потока.

Экспериментальное изучение отдельных зон на физических моделях. Экспериментальное определение поля скоростей в каждой зоне проводится на физической модели, причем не обязательно модели всего аппарата. Так, например, проточный аппарат заменялся тремя моделями: уступа (а), трубы (б), области сужения потока (в) (рис. 3.5) [6]

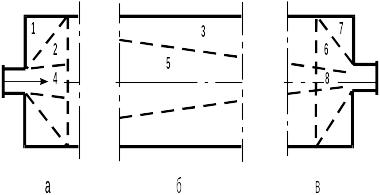
Рис. 3.5. Схема физических моделей проточного аппарата: а - уступ, б - труба, в - область сужения потока.

Глава 4. Межфазный перенос субстанций

В зависимости от вида переносимой субстанции можно выделить массо-, тепло-, импульсопередачу.

Перенос от границы раздела фаз к ядру фазы или от ядра к границе в зависимости от вида субстанции называют массо-, тепло- или импульсоотдачей.

4.1. Уравнения массо-, тепло- и импульсоотдачи

4.1.1. Локальная форма уравнений

Рассмотрим элементарный, бесконечно малый участок межфазной поверхности dF. Прямоугольную систему координат расположим так (рис. 4.1), чтобы плоскость X - Z совмещалась с поверхностью раздела фаз, а ось Х - с направлением движения рассматриваемой фазы (поскольку участок межфазной поверхности выбран бесконечно малым, его можно считать плоским).

Рис. 4.1. Перенос субстанций через элементар­ный участок межфазной поверхности dF

Поток субстанции через границу раздела фаз будет осуществляться по нормали к ней, т.е. вдоль оси Y. Рассмотрим потоки субстанций за счет молекулярного и турбулентного механизмов переноса, которые будем называть в зависимости от вида соответствующих коэффициентов переноса диффузионным потоком массы , вязким потоком импульса (тензор вязких напряжений), потоком тепла за счет теплопроводности . В отличие от полных потоков данные величины не учитывают конвективный механизм переноса субстанций, несмотря на то, что он может присутствовать. Продемонстрируем вывод уравнений на примере теплоотдачи. Проекцию теплового потока за счет теплопроводности на ось Y в соответствии с (1.42) можно записать, рассматривая изменение этой величины только в направлении у, в виде

. (4.1)

Введем величину q*(y), характеризующую отношение потока на расстоянии y от межфазной границы к граничному значению:

. (4.2)

С использованием величины q* перепишем уравнение (4.1), решим его относительно dT и проинтегрируем, используя модель пограничного слоя, от границы раздела фаз до внешней границы слоя. Температура при этом изменится от значения на межфазной поверхности (Т^г) до значения в ядре фазы (Т^я). Следует иметь в виду, что коэффициент турбулентной теплопроводности является функцией расстояния от границы раздела фаз _т(y) и не может быть вынесен из под интеграла

. (4.3)

Решив уравнение (4.3) относительно q_у^тг, получим уравнение теплоотдачи. Выражение в его правой части, стоящее перед разностью температур, носит название коэффициента теплоотдачи:

. (4.4)

Аналогичным образом могут быть получены уравнения массо- и импульсоотдачи, что позволяет использовать единую форму их представления и определить соответствующие коэффициенты:

, (4.5)

, (4.6)

, (4.7)

, (4.8)

, (4.9)

. (4.10)

Здесь j_iy^gг, q_y^тг, _yx^вг - потоки вещества компонента i, тепла и импульса через границу раздела фаз в системе отсчета, связанной с этой границей, без учета конвективных составляющих; _i или , - коэффициенты массо-, тепло- и импульсоотдачи соответственно; _i^я, c_i^я, Т^я, W_x^я - значения химического потенциала, концентрации компонента i, температуры, скорости в ядре фазы; _i^г, c_i^г, Т^г, W_х^г - значения этих величин для данной фазы в непосредственной близости от границы раздела фаз; _g, _т, _г - толщины диффузионного, теплового и гидродинамического пограничных слоев.

Разница значений химических потенциалов или концентраций, температур, скоростей у границы раздела фаз и в ядре фазы носит название движущей силы массо-, тепло- и импульсоотдачи. Отличие ее от нуля является необходимым условием протекания соответствующего процесса.

, моль²/Дж м²с; (4.11)

, м/с; (4.12)

, Вт/м²К; (4.13)

, кг/м²с . (4.14)

Коэффициент массоотдачи - количество вещества компонента i, переносимое от границы раздела фаз в ядро фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности в расчете на единицу движущей силы.

Коэффициент теплоотдачи характеризует количество тепла, переносимое от границы раздела фаз к ядру фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности в расчете на единицу движущей силы.

Коэффициент импульсоотдачи характеризует количество импульса Р_x, переносимое от границы раздела фаз к ядру фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности в расчете на единицу движущей силы.