2.3. Бином Ньютона. Полиномиальная формула

Бином Ньютона – это формула, выражающая выражение в виде многочлена. Эта формула имеет вид:

где число сочетаний из n элементов по k.

Широко известные формулы сокращённого умножения квадрата суммы и разности, куба суммы и разности, являются частными случаями бинома Ньютона. Если степень n бинома Ньютона невысока, коэффициенты многочлена могут быть найдены не расчётом по формуле количества сочетаний, а с помощью так называемого треугольника Паскаля.

Треугольник Паскаля имеет вид:

1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

………………………………….

Формула бинома Ньютона может быть обобщена для произвольного числа слагаемых:

, где

Пример. В разложении найти члены, содержащие х^a, если k = 3, p = 2, n = 8, a = 9.

По формуле бинома Ньютона имеем:

.

C учётом числовых значений:

.

В принципе, можно записать разложение этого выражения в многочлен, определить коэффициенты либо непосредственно, либо из треугольника Паскаля (степень бинома сравнительно невелика), однако, делать это не обязательно, так как необходимо найти только член разложения, содержащий х⁹.

Найдем число i, соответствующее этому члену:

Находим:

Пример. В разложении найти члены, содержащие x^g. т = 9, g = 6.

По обобщённой формуле бинома Ньютона получаем:

Для нахождения полного разложения необходимо определить все возможные значения n_i, однако, это связано с громадными вычислениями. Поскольку надо найти только члены, содержащие х⁶, то n₁ = 6, а сумма всех четырёх значений n равна 9. Значит, сумма n₂ + n₃ + n₄ = 3.

Рассмотрим возможные значения этих величин (см. табл. 2.1).

Таблица 2.1

n2	0	0	3	1	1	0	2	0	2	1
n3	0	3	0	2	0	1	1	2	0	1
n4	3	0	0	0	2	2	0	1	1	1

Искомые члены разложения:

3. Алгебраические структуры

3.1. Внутренние бинарные операции на множестве

Определение 3.1. Кортежем длины называется множество, для которого указан порядок следования его элементов.

Обозначение:

Определение 3.2. Кортеж длины называется упорядоченной парой.

Определение 3.3. Упорядоченные пары и называются равными, если равны соответствующие элементы этих пар:

Определение 3.4. Прямым (декартовым) произведением двух множеств и называется множество упорядоченных пар , где

.

Замечание. Множество называется прямым квадратом множества A.

Определение 3.5. Бинарным отношением , заданным на множестве А, называется подмножество прямого квадрата этого множества. Тот факт, что элементы находятся друг с другом в отношении , обозначается записью вида

или

Примеры.

1. Рассмотрим множество всех прямых плоскости. Зафиксируем некоторую прямую и выделим те прямые плоскости, которые параллельны . Все эти прямые будут образовывать отношение параллельности на множестве прямых плоскости.

2. Рассмотрим на множестве N натуральных чисел пары чисел Введём отношение следующим образом:

Введённое таким образом бинарное отношение позволит выделить на множестве натуральных чисел пары взаимнопростых чисел.

Определение 3.6. Множество всех первых элементов пар, находящихся в отношении , называется областью определения отношения и обозначается :

Множество всех вторых элементов пар, находящихся в отношении , называется областью значения отношения и обозначается :

Объединение областей определения и значения бинарного отношения называется областью бинарного отношения .

Примеры.

1. Рассмотрим бинарное отношение , заданное следующим образом: . Здесь область определения и область значений отношения такие: Областью бинарного отношения будет множество

2. На множестве действительных чисел R рассмотрим бинарное отношение : . Здесь

Определение 3.7. Пусть на множестве A заданы бинарные отношения и . Бинарные отношения и будем называть равными, если эти бинарные отношения равны как множества.

Определение 3.8. Инверсией бинарного отношения называется бинарное отношение

Пример. Пусть

,

тогда

Теорема 3.1. Пусть – бинарное отношение, заданное на множестве А. Тогда справедливы следующие утверждения:

1. 

2. 

3. 

Определение 3.9. Бинарное отношение , заданное на множестве А, называется рефлексивным, если каждый элемент этого множества состоит в отношении с самим собой:

.

Примеры.

1. Отношение параллельности, заданное на множестве прямых плоскости.

2. Отношение равенства (подобия, тождества), заданное на некотором множестве.

3. Отношение делимости, заданное на множестве целых чисел

Определение 3.10. Бинарное отношение , заданное на множестве А, называется антирефлексивным, если во множестве А существует хотя бы один элемент, который не состоит в отношении с самим собой:

Примеры.

1. Отношение перпендикулярности, заданное на множестве прямых плоскости.

2. Отношение неравенства, заданное на некотором множестве.

3. Отношения заданные на некотором числовом множестве.

Определение 3.11. Бинарное отношение , заданное на множестве А, называется транзитивным, если для любых элементов из того что и следует, что

Примеры.

1. Отношение равенства, заданное на некотором множестве.

2. Отношение делимости, заданное на множестве целых чисел.

3. Отношение параллельности, заданное на множестве прямых плоскости.

4. Отношения заданные на некотором числовом множестве.

Определение 3.12. Бинарное отношение , заданное на множестве А, называется симметричным, если для любых элементов из того что следует, что

Примеры.

1. Отношение параллельности, заданное на множестве прямых плоскости.

2. Отношение перпендикулярности, заданное на множестве прямых плоскости.

3. Отношение равенства, заданное на некотором числовом множестве.

Определение 3.13. Бинарное отношение , заданное на множестве А, называется антисимметричным, если для любых элементов из того что и следует, что

Примеры.

1. Отношение включения, заданное на некотором множестве.

2. Отношения заданные на некотором числовом множестве.

Определение 3.14. Бинарное отношение , заданное на множестве А, называется связанным на множестве А, если для любых элементов из того что следует, что либо Иначе говоря, бинарное отношение , заданное на множестве А, называется связанным на множестве А, если для любых элементов либо либо либо

Примеры.

1. Отношения заданные на некотором числовом множестве.

2. Пусть множество всех подмножеств множества Отношение включения на множестве является связанным на множестве

Замечание. Для того чтобы определить, каким свойством обладает бинарное отношение, необходимо воспользоваться непосредственно определениями 3.9–3.14.

Определение 3.15. Бинарное отношение , заданное на множестве А, называется отношением эквивалентности, если оно рефлексивно, транзитивно и симметрично.

Примеры.

1. Отношение параллельности, заданное на множестве прямых плоскости.

2. Отношение равенства (подобия, тождества), заданное на некотором множестве.

3. Это отношение называется отношением сравнения по данному модулю Действительно:

   1. рефлексивность:

2. симметричность:

3. транзитивность:

4. Отношение подобия, заданное на множестве треугольников данной плоскости.

Определение 3.16. Пусть бинарное отношение , заданное на множестве А, является отношением эквивалентности, и некоторый фиксированный элемент этого множества. Классом эквивалентности, порождённым элементом называется множество элементов, принадлежащих множеству А, таких, что каждый из этих элементов находится в отношении с элементом

Обозначение:

Определение 3.17. Любой элемент класса эквивалентности называется представителем этого класса. Множество представителей всех классов эквивалентности по данному отношению эквивалентности, взятых по одному и только по одному, называется полной системой представителей.

Примеры.

1. Пусть на множестве прямых плоскости рассматривается отношение параллельности. В этом случае классами эквивалентности являются пучки параллельных прямых. Полной системой представителей классов эквивалентности по отношению параллельности на множестве прямых плоскости будет множество прямых плоскости, не параллельных друг другу.

2. В один и тот же класс эквивалентности, порождённый отношением сравнения по данному модулю на множестве целых чисел, войдут числа, равноостаточные при делении на данное фиксированное целое число Таких классов эквивалентности будет ровно Эти классы эквивалентности называются классами вычетов по данному модулю

Определение 3.18. Фактормножеством множества А по отношению эквивалентности называется множество всех классов эквивалентности по данному бинарному отношению.

Обозначение:

Пример. Пусть на множестве точек плоскости бинарное отношение задано следующим образом: точка находится в отношении с точкой , если и одинаково удалены от некоторой фиксированной точки плоскости. Покажем, что заданное таким образом бинарное отношение является отношением эквивалентности, найдём классы эквивалентности и фактормножество.

Будем обозначать расстояние от точки до точки записью вида

1. Бинарное отношение является рефлексивным:

2. Бинарное отношение является симметричным:

3. Бинарное отношение является транзитивным:

Таким образом, в соответствии с определением 3.15, бинарное отношение является отношением эквивалентности.

Класс эквивалентности , порождённый точкой по отношению эквивалентности , будет представлять собой множество точек плоскости таких, что расстояние от этих точек до точки будет равно расстоянию т. е. – множество точек окружности с центром в точке и радиусом Таких классов эквивалентности будет бесчисленно много. Фактормножество , очевидно, представляет собой всю плоскость .

Теорема 3.2. Пусть отношение эквивалентности, заданное на непустом множестве А. Тогда каждый элемент множества А входит в точности в один и тот же класс эквивалентности.

Замечание. Теорему 3.2 можно переформулировать следующим образом: два класса эквивалентности либо не пересекаются, либо совпадают.

Определение 3.19. Бинарное отношение , заданное на множестве А, называется отношением порядка на А, если оно транзитивно и антисимметрично.

Определение 3.20. Бинарное отношение , заданное на множестве А, называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно.

Определение 3.21. Бинарное отношение , заданное на множестве А, называется отношением строгого порядка, если оно транзитивно и антирефлексивно.

Замечание. В определении 3.21 явно не прослеживается требование антисимметричности бинарного отношения, но это свойство непосредственно следует из свойств транзитивности и антисимметричности. Относительно этого утверждения справедлива следующая теорема.

Теорема 3.3. Пусть бинарное отношение , заданное на множестве А, транзитивно и антирефлексивно. Тогда антисимметрично на множестве А.

Примеры.

1. Отношение включения, заданное на множестве является отношением нестрогого порядка.

2. Отношения и заданные на множестве действительных чисел R, являются соответственно отношениями строгого и нестрогого порядка.

3. Отношение делимости, заданное на множестве натуральных чисел является отношением нестрого порядка.

Определение 3.22. Отношение порядка, заданное на множестве А, называется отношением линейного порядка, если оно связанное. Отношение порядка, не являющееся линейным, называется отношением частичного порядка.

Примеры.

1. Отношение заданное на множестве действительных чисел R, является отношением линейного порядка.

2. Отношение лексикографического порядка в словарях русского языка является линейным порядком.

3. Отношение включения, заданное на множестве всех подмножеств данного множества, является частичным порядком.

4. Пусть бинарное отношение задано на множестве людей следующим образом: человек находится в отношении с человеком если по меньшей мере на 2 года моложе Бинарное отношение является отношением частичного порядка. Покажем это:

1. если человек находится в отношении с человеком а человек находится в отношении с человеком то и человек также будет находиться в отношении с человеком поскольку будет моложе его, по крайней мере, на четыре года, т. е. бинарное отношение является транзитивным;

2. очевидно, что бинарное отношение является антирефлексивным. Тогда, в соответствии с определением 3.21, бинарное отношение является отношением строгого порядка;

3. Бинарное отношение не является связанным. Действительно, если, к примеру, человеку 21 год, а человеку 22 года, то, очевидно, но из этого, тем не менее, не следует, что человек находится в отношении с человеком или человек находится в отношении с человеком Таким образом, в соответствии с определением 3.22, бинарное отношение является отношением частичного порядка.

Определение 3.23. Упорядоченным множеством называется пара где А – непустое множество элементов любой природы, отношение порядка на множестве А. Если отношение линейного порядка, то множество А называется линейно упорядоченным. Если порядок является частичным, то множество А называется частично упорядоченным.

Пример.

1. Множество действительных чисел R по отношению является линейно упорядоченным множеством.

2. Множество всех подмножеств данного множества с введённым порядком включения является частично упорядоченным множеством.

Пусть A и B – два множества.

Определение 3.24. Бинарное отношение заданное на прямом произведении называется отображением множества А на множество В, если для любых элементов из области бинарного отношения из того что и следует, что

Определение 3.25. Отношение заданное на прямом произведении называется инъективным отображением множества А на множество В (отображением А в В), если для любых элементов из области отношения из того что и следует, что

Определение 3.26. Бинарной алгебраической операцией, заданной на непустом множестве А, называется инъективное отображение прямого квадрата во множество А.

Замечания.

1. Из определения 3.26 следует, что бинарной операцией, заданной на множестве А, называют отображение, ставящее в соответствие каждой упорядоченной паре определённый элемент c из множества А.

2. Понятие бинарной операции является частным случаем понятия отображения.

3. Обычно бинарную операцию обозначают некоторым символом: При этом записывают

Определение 3.27. Отображение й прямой степени множества A во множество А называется местной операцией, заданной на множестве А, а число n называется рангом операции.

Замечания.

1. Если в определении 3.27 то операция называется нульместной.

2. Если в определении 3.27 то операция называется унарной.

3. Ранг бинарной операции, очевидно, равен двум.

Примеры.

1. Операции сложения, умножения, вычитания можно рассматривать как бинарные алгебраические операции на множестве R действительных чисел.

2. Умножение квадратных матриц порядка n является бинарной алгебраической операцией, заданной на множестве квадратных матриц порядка n.

3. Линейные операции с элементами арифметического 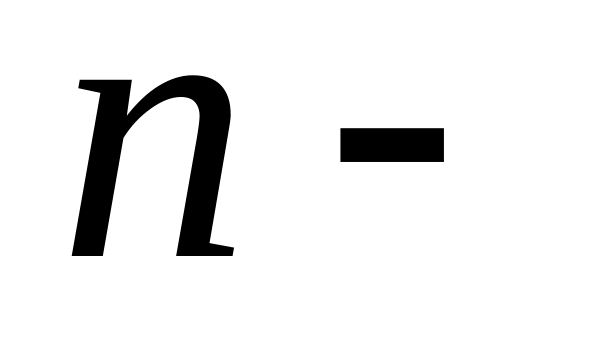мерного векторного пространства являются бинарными операциями в этом пространстве.

4. Векторное произведение векторов трёхмерного евклидова пространства является бинарной операцией на множестве трёхмерных векторов.

5. Рассмотрим множество N натуральных чисел и действия с ними. Вычитание не будет являться бинарной алгебраической операцией на множестве N, поскольку не для всех натуральных чисел их разность будет натуральным числом.

6. Операция деления рациональных чисел не является бинарной алгебраической операцией, поскольку упорядоченной паре нельзя поставить в соответствие какое-либо число из множества

Замечание. Если на множестве А задана бинарная алгебраическая операция , то говорят, что множество А замкнуто относительно операции .

Пусть и бинарные алгебраические операции, заданные на множестве А. Рассмотрим виды бинарных операций.

Определение 3.28. Бинарная алгебраическая операция называется коммутативной на множестве А, если для любых элементов имеет место равенство

Определение 3.29. Бинарная алгебраическая операция называется ассоциативной на множестве А, если для любых элементов имеет место равенство

Замечание. Если операция ассоциативна на множестве А, то скобки в равенстве можно опускать.

Определение 3.30. Бинарная алгебраическая операция называется дистрибутивной относительно бинарной алгебраической операции , если для любых элементов имеет место равенство

Примеры.

1. Операции сложения, умножения на множестве R действительных чисел коммутативны и ассоциативны.

2. На множестве R действительных чисел операция умножения дистрибутивна относительно операции сложения.

3. Рассмотрим множество всех подмножеств некоторого универсального множества U, а также операции объединения и пересечения Эти бинарные алгебраические операции коммутативны, ассоциативны и каждая из этих операций дистрибутивна относительно другой на .

4. Операция умножения квадратных матриц фиксированного порядка n ассоциативна, но не коммутативна на указанном множестве.

5. Векторное произведение векторов трёхмерного евклидова пространства не ассоциативно на множестве трёхмерных векторов.

6. Нахождение противоположного элемента для фиксированного элемента некоторого числового множества является унарной операцией.

7. Фиксация некоторого элемента в заданном множестве является нульместной операцией.

Определение 3.31. Элемент называется левым (правым) нейтральным относительно бинарной алгебраической операции , заданной на множестве А, если для любого элемента справедливо равенство

Определение 3.32. Элемент называется нейтральным относительно бинарной алгебраической операции , заданной на множестве А, если для любого элемента справедливы равенства т. е. элемент одновременно является левым нейтральным и правым нейтральным относительно бинарной операции .

Примеры.

1. Ноль является нейтральным элементом относительно операции сложения на всех числовых множествах, кроме множества натуральных чисел.

2. Единица является нейтральным элементом относительно операции умножения на всех числовых множествах.

3. Пустое множество Ø является нейтральным элементом относительно операции объединения на множестве всех подмножеств некоторого множества А.

4. Рассмотрим на множестве натуральных чисел N бинарную алгебраическую операцию Единица является правым нейтральным элементом, но не является левым нейтральным элементом множества N относительно введённой операции.

5. Множество чётных чисел относительно операции умножения не имеет нейтрального элемента.

Заметим, что если нейтральный (левый нейтральный, правый нейтральный) элемент относительно некоторой бинарной операции, заданной на множестве А, существует, то он единственный.

Пусть – бинарная операция на множестве А, относительно которой существует нейтральный элемент

Определение 3.33. Элемент называется левым (правым) симметричным к элементу относительно бинарной операции , если выполняется равенство

Определение 3.34. Элемент называется симметричным к элементу относительно бинарной операции , если выполняются равенства

При этом элементы называются взаимосимметричными.

Примеры.

1. Относительно операции сложения, заданной на множестве R действительных чисел, взаимосимметричными являются равные по модулю и противоположные по знаку действительные числа.

2. Относительно операции умножения на множестве рациональных чисел отличных от нуля, взаимосиметричными являются рациональное число и обратное ему рациональное число. Число ноль не имеет симметричного элемента относительно операции умножения.