3.10. Факторизация колец. Евклидовы кольца

Определение 3.71. Говорят, что элемент области целостности представим в виде произведения простых сомножителей единственным образом, если выполняются следующие условия:

1. где простые элементы кольца ,

2. если существует ещё одно разложение этого элемента на простые элементы то количества элементов в этих разложениях равны, и при соответствующей нумерации каждый ассоциирован с соответствующим

Определение 3.72. Кольцо называется факториальным, если оно является областью целостности и любой отличный от нулевого необратимый элемент этого кольца обладает однозначным разложением на простые множители.

Замечание. Поле – факториальное кольцо, поскольку оно не содержит необратимых элементов, отличных от нуля.

Теорема 3.26. Кольцо главных идеалов факториально.

Пример. Кольцо целых чисел факториально. Действительно, выше мы установили, что кольцо целых чисел является кольцом главных идеалов, что, в соответствии с предшествующей теоремой, и объясняет факториальность этого кольца.

Далее будем считать ноль натуральным числом.

Определение 3.73. Область целостности называется евкли-довым кольцом, если существует отображение основного множества кольца во множество натуральных чисел удовлетворяющее следующим условиям:

1. для любых элементов где существует пара элементов 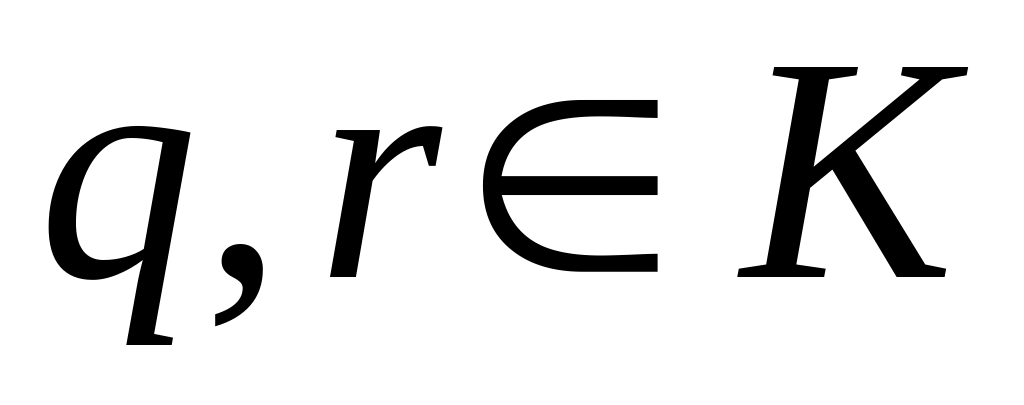такая, что справедливо равенство где

2. для любого элемента равенство выполняется тогда и только тогда, когда

Пример. Рассмотрим кольцо целых чисел . Это кольцо является евклидовым. Отображение

,

удовлетворяющее условиям 1), 2) определения 3.73, может быть задано следующим образом:

Теорема 3.27. Евклидово кольцо является кольцом главных идеалов.

Теорема 3.28. Евклидово кольцо факториально.

Пример. Рассмотрим кольцо целых гауссовых чисел и покажем, что это кольцо является евклидовым кольцом, кольцом главных идеалов и факториальным кольцом. Как установлено выше, кольцо является областью целостности. Зададим отображение

следующим образом: каждому элементу поставим в соответствие натуральное число

Проверим справедливость условий определения 3.73.

1. Пусть произвольные элементы множества и выполняется равенство

где в общем случае числа и рациональные. Очевидно, существуют такие целые числа и что Тогда

Поскольку числа и целые, число следовательно, Кроме того, а поскольку кольцо, то и

Тем самым мы показали, что в кольце существуют такие элементы и , что справедливо равенство

Покажем, что

Поскольку получим неравенство:

откуда следует, что

2. Пусть , тогда Очевидно, что тогда и только тогда, когда т. е.

Таким образом, кольцо целых гауссовых чисел, по определению, является евклидовым. В соответствии с утверждениями теорем 3.27 и 3.28, кольцо является кольцом главных идеалов и факториальным кольцом.

4. Кольцо целых чисел