3.8. Гомоморфизмы колец

Определение 3.57. Гомоморфизмом кольца в (на) кольцо называется отображение сохраняющее главные операции кольца т. е. для любых элементов имеют место следующие равенства:

1. 

2. 

3. 

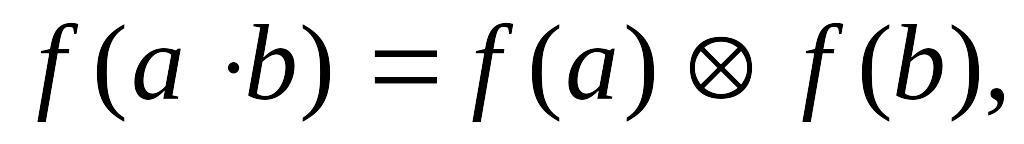
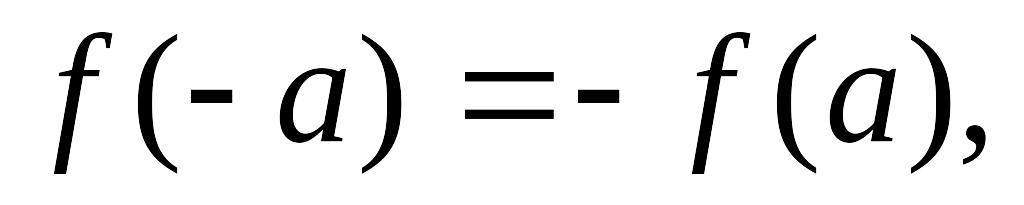
4. если и существуют.

Определение 3.58. Гомоморфизм кольца на кольцо называется эпиморфизмом.

Определение 3.59. Эпиморфизм кольца на кольцо называется изоморфизмом, если отображение является инъективным. При этом кольца называются изоморфными. Факт изомор-физма колец обозначают записью вида

Пример. Рассмотрим два кольца и , где множество квадратных матриц второго порядка вида – множество иррациональных чисел вида Покажем, что Для этого зададим отображение основного множества второго кольца в основное множество первого кольца по следующему правилу: Проверим справедливость условий 1)–4) из определения 3.57:

1. 

2. 

3. 

4. 

Таким образом, гомоморфизм колец. Несложно убедиться и в том что отображение инъективно. Таким образом,

Определение 3.60. Пусть гомоморфизм кольца в кольцо . Множество элементов кольца , которые отображаются в ноль кольца , называется ядром гомоморфизма:

Множество элементов кольца , которые имеют прообраз в кольце , называется образом гомоморфизма:

Определение 3.61. Пусть гомоморфизм кольца в кольцо . Тогда ядро гомоморфизма является идеалом кольца :

Теорема 3.21 (об эпиморфизме колец). Пусть эпиморфизм кольца на кольцо . Тогда факторкольцо изоморфно кольцу :

Пример. Рассмотрим кольцо , основным множеством которого является множество многочленов степени n с целыми коэффициентами:

а также кольцо целых чисел .

Покажем, что факторкольцо , где изоморфно кольцу

1. Зададим отображение следующим образом:

Покажем, что заданное отображение является эпиморфизмом кольца на кольцо

1. 

2. 

3. 

4)

Из 1)–4) следует, что отображение является гомоморфизмом. Поскольку любому целому числу соответствует многочлен из отображение является сюръекцией (отображением «на»). Следовательно, отображение является эпиморфизмом.

2. Найдём ядро эпиморфизма. По определению 3.60,

Следовательно, ядром эпиморфизма является множество многочленов, свободные члены которых равны нулю:

3. Найдём идеал кольца :

Таким образом, идеал кольца совпадает с ядром эпиморфизма

Тогда, по теореме об эпиморфизме колец, факторкольцо изоморфно кольцу

3.9. Кольца главных идеалов.

Делимость и ассоциированность в кольцах

Определение 3.62. Пусть произвольное кольцо, Главным идеалом кольца порождённым элементом называется наименьший идеал этого кольца, содержащий элемент Для обозначения используется запись

Замечание. Главный идеал, порождённый элементом в кольце всегда существует. Как множество, он представляет собой пересечение всех идеалов этого кольца, содержащих порождающий элемент.

Теорема 3.22 (о строении главного идеала области целостности). Пусть область целостности, Тогда главный идеал кольца имеет следующую структуру:

Замечание. Если ослабить условия теоремы 3.22 и убрать требование того, что кольцо является кольцом с единицей, то главный идеал этого кольца представляет собой следующее множество элементов кольца:

Определение 3.63. Кольцом главных идеалов называется область целостности, в которой каждый идеал является главным.

Пример. Рассмотрим кольцо целых чисел . Выше мы установили, что кольцо является областью целостности. Покажем, что это кольцо является кольцом главных идеалов. Пусть Возможно два взаимоисключающих случая: и Очевидно, что идеал в кольце целых чисел является главным. В идеале выберем наименьшее целое число Поскольку по определению идеала, для любого элемента произведение принадлежит множеству Рассмотрим произвольный элемент и поделим его на число с остатком:

откуда Поскольку и число также из Но это (в силу условия ) означает, что наименьшим числом в идеале является целое число что противоречит аналогичному предположению относительно числа Следовательно, и Тогда, в соответствии с теоремой о структуре главного идеала области целостности, идеал является главным идеалом кольца целых чисел. Таким образом, любой идеал кольца является главным.

Далее будем рассматривать коммутативные кольца .

Определение 3.64. Элемент называется делителем элемента , если существует такой элемент что выполняется равенство При этом говорят, что делит и записывают: .

Теорема 3.23. Отношение делимости в кольце является рефлексивным и транзитивным.

Определение 3.65. Элемент называется общим делителем элементов , если делит каждый из элементов

Определение 3.66. Элементы кольца называются ассоциированными в кольце , если делит и делит . При этом записывают:

Теорема 3.24. Отношение ассоциированности в кольце является отношением эквивалентности

Теорема 3.25. Пусть область целостности. Элементы ассоциированы тогда и только тогда, когда в кольце существует такой обратимый элемент что справедливо равенство

Пусть область целостности.

Определение 3.67. Тривиальными делителями элемента называется любой обратимый элемент кольца и любой элемент, ассоциированный с

Определение 3.68. Собственным делителем элемента называется любой его нетривиальный делитель.

Определение 3.69. Элемент области целостности называется составным (приводимым) в кольце, если он отличен от нуля кольца и его можно представить в виде произведения двух собственных делителей.

Определение 3.70. Элемент области целостности называется простым (неприводимым) в кольце, если он отличен от нуля кольца, необратим в кольце и имеет только тривиальные делители.

Замечания.

1. В соответствии с введёнными определениями основное множество области целостности разбивается на следующие классы:

1. ноль кольца ;

2. обратимые элементы кольца ;

3. простые элементы ;

4. составные элементы кольца .

2. В поле нет простых и составных элементов, поэтому основное множество поля разбивается только на два класса – 1) и 2).

Пример. Рассмотрим кольцо основным множеством которого является множество целых гауссовых чисел

Кольцо целых гауссовых чисел является областью целостности. При этом Рассмотрим элемент этого кольца – число Покажем, что составной элемент кольца Для этого воспользуемся определением 3.69.

Очевидно, что

Найдём все обратимые элементы кольца т. е. такие элементы которые удовлетворяют равенству

Это равенство равносильно системе уравнений

решая которую в целых числах, найдём возможные комбинации неизвестных:

или

или

Тогда обратимыми элементами кольца целых гауссовых чисел являются комплексные числа:

Найдём делители числа в кольце Для этого решим уравнение

Решение этого уравнения равносильно решению системы уравнений вида

целые корни которой представлены следующими комбинациями:

или

или

или

Следовательно, элемент можно представить, в частности, в виде произведения

Элементы и в кольце являются собственными делителями . Действительно, эти числа отличны от обратимых элементов кольца и не ассоциированы с что следует из неразрешимости уравнений

и

в целых числах.

Таким образом, элемент области целостности отличен от нулевого элемента и представим в виде произведения двух собственных делителей, т. е. является составным элементом кольца.