29. Что характеризуют кривые работы газожидкостного подъемника

Физика процесса движения газожидкостной смеси в вертикальной трубе.

При скважинной добыче нефти практически всегда происходит выделение газа. Для понимания механизмов подъема жидкости из скважин, для проектирования установок подъема и выбора необходимого оборудования, надо знать законы движения газожидкостных смесей (ГЖС) в трубах.

Качественную характеристику процесса движения газожидкостной смеси в вертикальной трубе легче уяснить из следующего простого опыта (рис. 1).

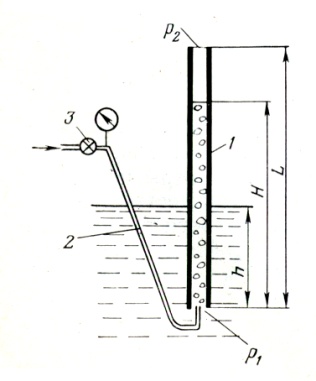
Рисунок 1. Схема газожидкостного подъемника

Здесь трубка 1 длиною L погружена под уровень жидкости неограниченного водоема на глубину h. К нижнему открытому концу трубки, который по аналогии с промысловой терминологией называется башмаком, подведена другая трубка 2 для подачи с поверхности сжатого газа. На трубке имеется регулятор расхода 3, с помощью которого можно установить желаемый расход газа.

Давление у башмака подъемной трубки 1 будет равно гидростатическому на глубине h, т.е. р₁=ρgh, и не будет изменяться от того, много или мало газа подается к башмаку. По трубке 2 подается газ, и в трубке 1 создается газожидкостная смесь средней плотности ρ_с , которая поднимается на некоторую высоту H. Поскольку внутренняя полость трубки 1 и наружная область являются сообщающимися сосудами, имеющими на уровне башмака одинаковые давления, то можно написать равенство

,

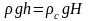откуда

Плотность смеси в трубке ρ_с зависит от расхода газа V. Чем больше V, тем меньше ρ_с . Следовательно, изменяя V, можно регулировать H. При некотором расходе V=V₁ величина H может достигнуть L. При V<V₁ H<L. При V>V₁ H>L и наступит перелив жидкости через верхний конец трубки 1. При дальнейшем увеличении V расход поступающей на поверхность жидкости q увеличится. Однако при непрерывном увеличении V расход жидкости не будет увеличиваться непрерывно, так как под воздействием неизменяющегося перепада давления 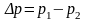( 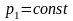, так как 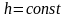), труба определенной длины L и диаметра d должна пропускать конечное количество жидкости, газа или газожидкостной смеси. Таким образом, при некотором расходе газа V=V₂ дебит достигает максимума .

Возможен другой крайний случай, когда к башмаку подъемной трубы подводится так много газа, что при постоянном перепаде давления 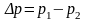будет идти только газ, и 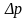будет расходоваться на преодоление всех сопротивлений, вызванных движением по трубе чистого газа. Расход этого газа пусть будет V=V₃ . Если к башмаку подать еще больший расход (V>V₃), то излишек газа не сможет пройти через подъемную трубу, так как ее пропускная способность при данных условиях (L, d, Δp) равна только V₃, и устремится мимо трубы, оттесняя от башмака жидкость. При этом расход жидкости будет равен нулю (q=0). Таким образом, из этого опыта можно сделать следующий вывод.

1. При V<V₁ q=0 (H < L).

2. При V=V₁ q=0 (H=L) (начало подачи).

3. При V₁<V<V₂ 0<q<q_max (H>L).

4. При V=V₂ q=q_max (точка максимальной подачи).

5. При V₂<V<V₃ 0<q<q_max.

6. При V=V₃ q=0 (точка срыва подачи).

Обычно правая ветвь кривой q(V) (рис. 2) пологая, левая крутая. Для всех точек кривой постоянным является давление p₁, так как погружение h в процессе опыта не изменялось. Существует понятие – относительное погружение ε=h/L. Таким образом, для данной кривой ее параметром будет величина относительного погружения ε.

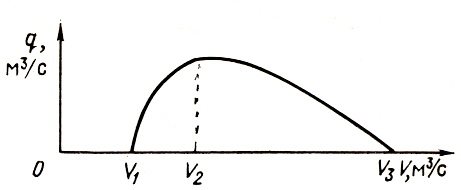
Рисунок 2. Зависимость подачи q газожидкостного подъемника от расхода газа V

Определим зависимость положения кривых q(V) от погружения. Поскольку на величину ε никаких ограничений не накладывалось, то при любых ε, лежащих в пределах 0<ε<1, вид соответствующих кривых q(V) будет одинаковый. При увеличении ε новые кривые q(V) обогнут предыдущие, так как с ростом h потребуется меньший расход газа для наступления перелива. По тем же причинам возрастет q_max , а точка срыва подачи на соответствующих кривых сместится вправо. При уменьшении ε все произойдет наоборот. Новые кривые q(V) расположатся внутри прежних и при ε=0 кривая q(V) выродится в точку. Другой предельный случай ε=1 (h=L; 100% погружения). В этом случае при бесконечно малом расходе газа произойдет перелив. Точка начала подачи сместится в начало координат. Кривая q(V) для ε=1 начнется в начале координат и обогнет все семейство кривых. Таким образом, каждый газожидкостный подъемник характеризуется семейством кривых q(V), каждый из которых будет иметь свой параметр ε (рис. 3).

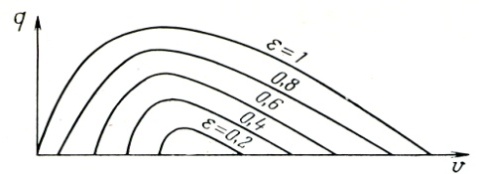
Рисунок 3. Семейство кривых q(V) для газожидкостного

подъемника данного диаметра

Определим зависимость кривых q(V) от диаметра трубы. Поскольку никаких ограничений на диаметр подъемной трубы и на ее длину не накладывалось, то аналогичное семейство кривых q(V) должно существовать для подъемников любого диаметра и любой длины. Каким образом расположится новое семейство кривых для трубы диаметром d₂>d₁ по отношению к прежним кривым. Увеличение диаметра потребует большого расхода газа, так как объем жидкости, который необходимо разгазировать для достижения данной величины ρ_с, при прочих равных условиях (h=const, L=const) возрастает пропорционально d². Пропускная способность трубы по жидкости, газу или газожидкостной смеси также возрастает. Поэтому для увеличенного диаметра будет существовать также семейство кривых q(V), все точки которого будут смещены вправо, в сторону увеличенных объемов, кроме одной точки, совпадающей с началом координат для кривой q(V) при ε=1 (рис. 4). В каждом из этих семейств и любых других, кривые q(V) при значениях ε, близких к единице и к нулю, не имеют практического значения.

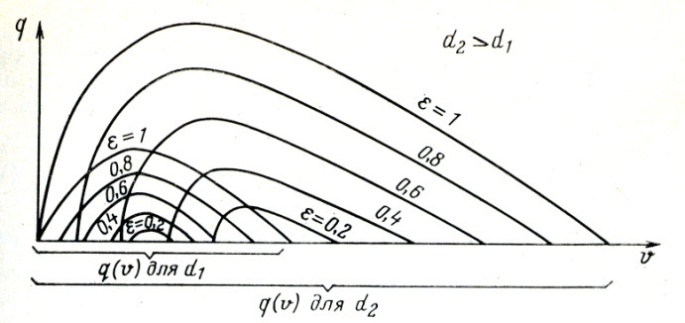
Рисунок 4. Семейство кривых q(V) для двух газожидкостных

подъемников различных диаметров