23. Давлений при движении газожидкостной смеси в скважине.

Уравнение баланса давления.

При проектировании или анализе работы установок для подъема жидкости из скважин, когда по НКТ движется ГЖС, основным вопросом является определение потерь давления, связанных с этим движением. Рассматривая некоторый участок вертикальной трубы, в которой движется ГЖС, можно записать

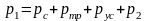, (1)

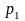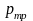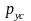где - давление в нижней части трубы, - давление, уравновешивающее гидростатическое давление столба ГЖС, - потери давления на преодоление сил трения при движении ГЖС, - потери давления на создание ускорения потока ГЖС, так как его скорость при движении в сторону меньших давлений увеличивается из-за расширения газа; 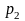- противодавление на верхнем конце трубы.

Уравнение (1) справедливо для всех случаев: короткой и длинной трубы, вертикальной и наклонной и является основным при расчете потерь давления и их составляющих.

При практических расчетах могут возникнуть две основные задачи, когда известно давление вверху и требуется определить давление внизу или наоборот. При этом все другие условия, такие как длина трубы, ее диаметр, расход поднимаемой жидкости, свойства жидкости и газа и другие, должны быть известны. Это так называемые прямые задачи. Но могут возникнуть и другие задачи, которые можно назвать обратными. Например, требуется определить расход поднимаемой жидкости при заданном перепаде давления 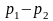. Или определить необходимое количество газа Г₀ для подъема заданного количества жидкости при заданном перепаде давления и ряд других задач. Во всех случаях необходимо знать слагаемые, входящие в уравнение баланса давления (1).

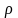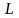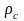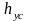Обозначим - плотность жидкости, - длина трубы по вертикали, - плотность ГЖС, - потеря напора на трение на участке трубы длиной в 1 м столба ГЖС, - потеря напора на ускорение на участке трубы длиной в 1 м столба ГЖС. С учетом этих обозначений уравнение (1) запишется в виде

. (2)

Разделив обе части равенства (2) на 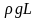, найдем

. (3)

Обозначим через

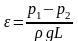, (4)

который является действующим перепадом давления, выраженным в метрах столба поднимаемой жидкости, отнесенным к 1 м длины трубы.

При 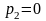(истечение в атмосферу) величина совпадает с тем относительным погружением при рассмотрением физической характеристики процесса движения ГЖС.

Выражение (4) является более общим, так как учитывает противодавление .

Уравнение (2) может быть записано в дифференциальной форме при

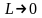
(5)

или в конечных разностях

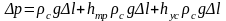. (6)

Величины , 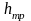, зависят от термодинамических условий потока, изменяющихся с глубиной, и в первую очередь существенно зависят от давления. Эти условия непрерывно изменяются вдоль трубы и их аналитический учет достаточно сложен. Задача сводится к интегрированию уравнения (5) в пределах от 0 до L либо к численному суммированию приращений давления, определяемых (6), также в пределах от 0 до L.

Если для таких коротких участков трубы рассчитать падение давления 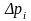, то общий перепад составит сумму

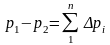, (7)

где

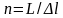. (8)

Из (7) следует, что если известно давление вверху , то

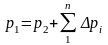. (9)

Если известно давление внизу , то

. (10)

Таким образом, задача сводится к расчету потерь давления на коротких участках подъемника при заданных параметрах движения (q, d, Г, ρ и пр.) и последующем их суммировании. Очевидно, чем больше n, т.е. чем меньш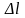е , тем точнее будет такое решение.