Действия с матрицами

ЗАДАНИЕ 1. Основные матричные операции.

По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.

Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Операция умножения матрицы на матрицу определяется следующим образом. Пусть заданы две матрицы А и В, причем число столбцов первой из них равно числу строк второй. Если

, ,

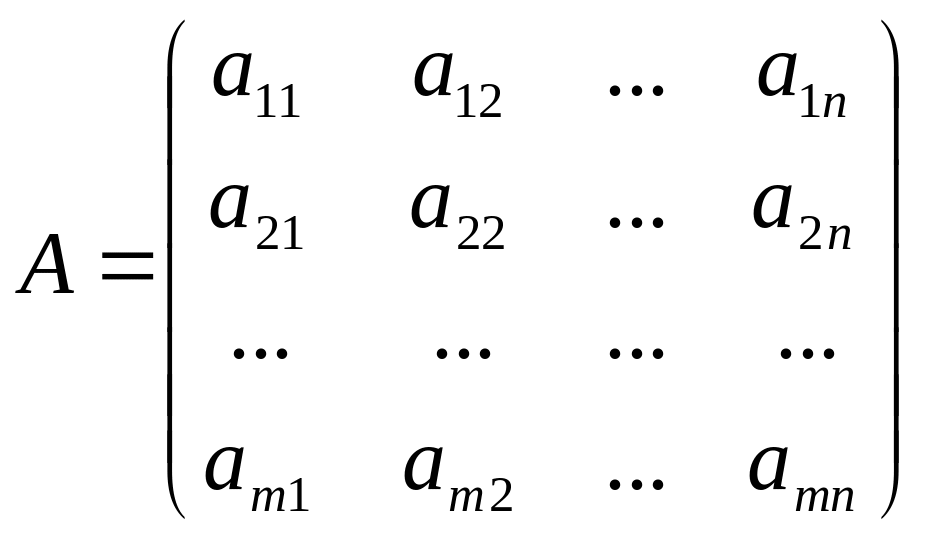то произведением матриц А и В называется матрица

,

элементы которой вычисляются по формуле

c_ij = a_i1b_1j + a_i2b_2j + … + a_inb_nj, i = 1,…, m, j = 1,..., k.

ЗАДАНИЕ 2. Транспонирование и вычисление обратной матрицы.

Матрица, получившаяся из матрицы А заменой строк столбцами, называется транспонированной по отношению к матрице А и обозначается А^Т.

Квадратная матрица А называется обратимой, если существует квадратная матрица Х, удовлетворяющая соотношению АХ = ХА = Е, т.е. АА^-1 = А^-1А = Е.

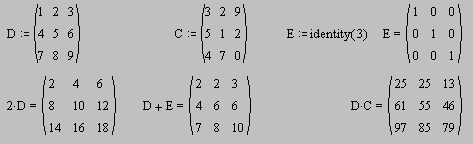
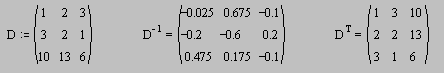
ЗАДАНИЕ 3. Вычисление определителей.

Пусть А – квадратная матрица порядка n, n > 1:

.

Определителем квадратной матрицы А порядка n, n > 1, называется число

где – определитель квадратной матрицы порядка n–1, полученной из матрицы А вычеркиванием первой строки и j-го столбца.

Из приведенного определения легко получить простое выражение определителя квадратной матрицы второго порядка:

Символьное вычисление определителя матрицы второго порядка:

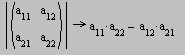
Числовой пример:

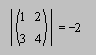
Матричная форма записи линейных систем. Решение матричных систем

Рассмотрим систему линейных алгебраических уравнений относительно n неизвестных x₁, x₂, …, x_n:

Эта система в «свернутом» виде может быть записана в виде

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде Ax = b, где

Если матрица системы невырождена (матрица, определитель которой отличен от нуля), то у нее существует обратная матрица и тогда решение системы легко получить, умножив обе части уравнения Ax = b слева на матрицу А^-1:

A^-1(Ax) = A^-1b, а поскольку A^-1A = E и Ex = x, то x = A^-1b.

ЗАДАНИЕ 4. Решение системы трех линейных уравнений относительно трех неизвестных.

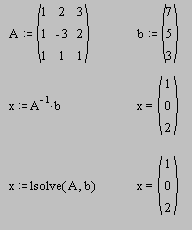
ЗАДАНИЕ 5. Решение системы линейных алгебраических уравнений по формулам Крамера.

При решении задач линейной алгебры необходимость вычислять определитель возникает достаточно часто. Наиболее распространенные приложения определителя – исследование и решение линейных систем.

Ниже приведен фрагмент рабочего документа MathCAD, содержащий решение линейной системы

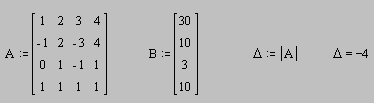
Определитель отличен от нуля, т.е. система имеет единственное решение.

Замечание. Для вычислений определителей Δ1, Δ2, Δ3, Δ4 проще всего скопировать матрицу А в буфер обмена, затем щелкнуть по кнопке в панели , вставить в помеченной позиции матрицу из буфера обмена (<Ctrl>+<C>) и затем заменить элементы соответствующего столбца элементами столбца правых частей.

Контрольные вопросы

9. Расскажите об основных элементах панели инструментов по работе с матрицами в MathCAD.

10. Какова взаимосвязь между матричной и обычной формами записи системы линейных уравнений?

11. В чем состоит метод Крамера решения систем линейных уравнений?

12. Как вычислить обратную матрицу, определитель в MathCAD?