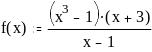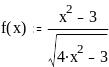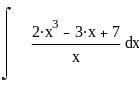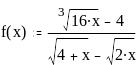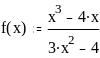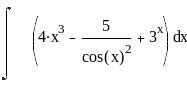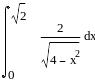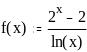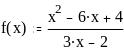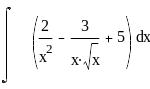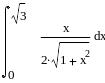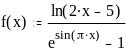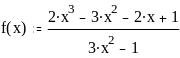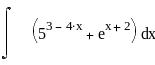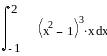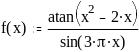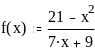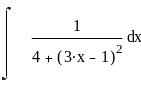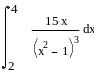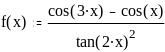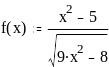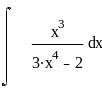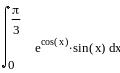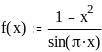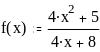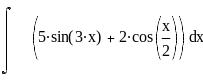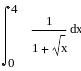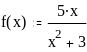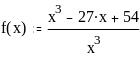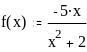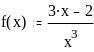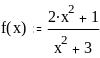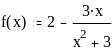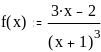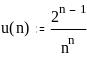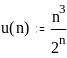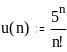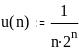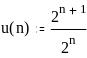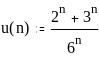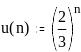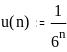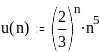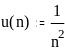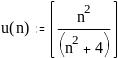- •Технический колледж Методические рекомендации
- •Математический пакет MathCad
- •Содержание
- •Пояснительная записка
- •Введение
- •Практическое занятие по теме: Простейшие вычисления и операции в MathCad
- •Контрольные вопросы
- •Практическое занятие по теме: Определение и вычисление значения функции в точке
- •Контрольные вопросы
- •Практическое занятие по теме: Работа с документами в MathCad
- •Контрольные вопросы
- •Практическое занятие по теме: Решение задач элементарной математики в MathCad
- •Преобразование алгебраических выражений
- •Определение, построение таблиц значений и графиков функций
- •Символьное решение уравнений и систем
- •Контрольные вопросы
- •Практическое занятие по теме: Задачи линейной алгебры
- •Действия с матрицами
- •Матричная форма записи линейных систем. Решение матричных систем
- •Контрольные вопросы
- •Практическое занятие по теме: Дифференциальное и интегральное исчисление
- •Контрольные вопросы
- •Практическое занятие по теме: Исследование функции и построение графиков
- •Вертикальные и наклонные асимптоты
- •Исследование функции с помощью производной
- •Исследование функции с использованием второй производной
- •Контрольные вопросы
- •Практическое занятие по теме: Числовые ряды
- •Основные понятия. Ряды с неотрицательными членами
- •Знакопеременные ряды
- •Контрольные вопросы
- •Приложение Задания для самостоятельной работы
- •Литература
Знакопеременные ряды
Если в
последовательности {un}
бесконечно много положительных и
отрицательных членов, то ряд
![]() называется знакопеременным.
Ряд
называется знакопеременным.
Ряд
![]() называется знакочередующимся.
Для знакопеременных рядов введено
понятие абсолютной сходимости. Ряд
называется абсолютно
сходящимся,
если сходится ряд
называется знакочередующимся.
Для знакопеременных рядов введено
понятие абсолютной сходимости. Ряд
называется абсолютно
сходящимся,
если сходится ряд
![]() .
Если ряд
расходится, а ряд
сходится, то говорят, что ряд
сходится
условно.
Справедливо следующее утверждение.
.
Если ряд
расходится, а ряд
сходится, то говорят, что ряд
сходится
условно.
Справедливо следующее утверждение.
Теорема Лейбница.
Если
последовательность
![]() стремится к нулю, монотонно убывая,
стремится к нулю, монотонно убывая,
![]() то ряд
то ряд
![]() сходится.
сходится.
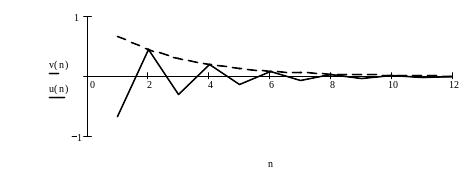
Ниже приведен фрагмент рабочего документа MathCAD с исследованием на сходимость знакопеременных рядов.
![]()
![]()
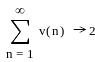
![]()
Контрольные вопросы
Дать определение числового ряда, его сходимости.
Сформулировать основные признаки сходимости числовых рядов.
Как с помощью MathCAD определить сумму числового ряда?
Как с помощью системы MathCAD определить сходимость или расходимость числового ряда?
Приложение Задания для самостоятельной работы
Задание 1. Вычислить значение выражения
0,7835

Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
Вариант 4 |
|
Вариант 5 |
|
Вариант 6 |
|
Вариант 7 |
|
Задание 2. Вычислить значение функции в заданной точке, построить график функции.
 при x = 0,128
при x = 0,128
 при x = 0,56
при x = 0,56
 при x = 1
при x = 1
 при x = 1,3
при x = 1,3
Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
Вариант 4 |
|
Вариант 5 |
|
Вариант 6 |
|
Вариант 7 |
|
Задание 3. Сохраните созданные вами документы в папку «C:\ Новикова \ № Вашей группы \ Фамилия».
Задание 4. Решение задач элементарной математики в MathCAD.
Упростите выражение
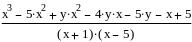
Раскройте скобки и приведите подобные слагаемые в выражении
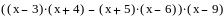
Разложите на множители выражение
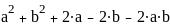
Решите графически уравнение

Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
Вариант 4 |
|
Вариант 5 |
|
Вариант 6 |
|
Вариант 7 |
|
Задание 5. Действия с матрицами.
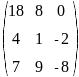
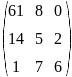
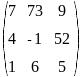
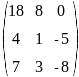
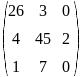
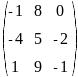
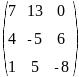
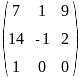
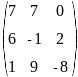
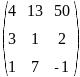
Транспонируйте матрицу и найдите обратную ей:
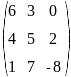
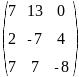
Вычислите определитель:

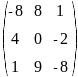
Решите систему трех линейных уравнений:

Найдите по формулам Крамера решение системы:

Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
Вариант 4 |
|
Вариант 5 |
|
Вариант 6 |
|
Вариант 7 |
|
Задание 6. Дифференциальное и интегральное исчисление.
Найдите предел функции f(x) в точке x = 4:
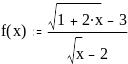
Вычислите производную функции:
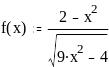
Вычисление интегралов:
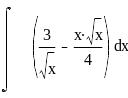
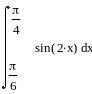
Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
Вариант 4 |
|
Вариант 5 |
|
Вариант 6 |
|
Вариант 7 |
|
Задание 7. Исследование функции и построение графиков
Изобразите график заданной функции и подтвердите построение аналитическим исследованием: найдите координаты точек пересечения с координатными осями; найдите и постройте наклонные асимптоты. Запишите уравнения вертикальных асимптот.
Изобразите график заданной функции и подтвердите построение аналитическим исследованием: постройте график производной, найдите нули производной. Найдите координаты точек экстремума.
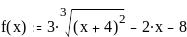
Изобразите график заданной функции и подтвердите построение аналитическим исследованием: постройте график второй производной, найдите нули второй производной. Найдите координаты точек перегиба, если они есть.
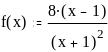
Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
Вариант 4 |
|
Вариант 5 |
|
Вариант 6 |
|
Вариант 7 |
|
Задание 8. Числовые ряды.
Исследуйте на сходимость числовые ряды:

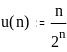
Исследуйте на сходимость знакопеременный ряд:

Вариант 1 |
|
Вариант 2 |
|
Вариант 3 |
|
Вариант 4 |
|
Вариант 5 |
|
Вариант 6 |
|
Вариант 7 |
|











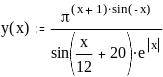 при x = 3,8
при x = 3,8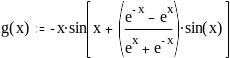 при x = 0,586
при x = 0,586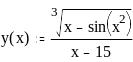 при x = 3,33
при x = 3,33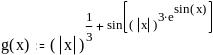 при x = -0,35
при x = -0,35