
- •Технический колледж Методические рекомендации
- •Математический пакет MathCad
- •Содержание
- •Пояснительная записка
- •Введение
- •Практическое занятие по теме: Простейшие вычисления и операции в MathCad
- •Контрольные вопросы
- •Практическое занятие по теме: Определение и вычисление значения функции в точке
- •Контрольные вопросы
- •Практическое занятие по теме: Работа с документами в MathCad
- •Контрольные вопросы
- •Практическое занятие по теме: Решение задач элементарной математики в MathCad
- •Преобразование алгебраических выражений
- •Определение, построение таблиц значений и графиков функций
- •Символьное решение уравнений и систем
- •Контрольные вопросы
- •Практическое занятие по теме: Задачи линейной алгебры
- •Действия с матрицами
- •Матричная форма записи линейных систем. Решение матричных систем
- •Контрольные вопросы
- •Практическое занятие по теме: Дифференциальное и интегральное исчисление
- •Контрольные вопросы
- •Практическое занятие по теме: Исследование функции и построение графиков
- •Вертикальные и наклонные асимптоты
- •Исследование функции с помощью производной
- •Исследование функции с использованием второй производной
- •Контрольные вопросы
- •Практическое занятие по теме: Числовые ряды
- •Основные понятия. Ряды с неотрицательными членами
- •Знакопеременные ряды
- •Контрольные вопросы
- •Приложение Задания для самостоятельной работы
- •Литература
Контрольные вопросы
Дайте определения точек экстремума функции, точек перегиба.
Дайте определения четной и нечетной функции. Какими свойствами обладают их графики?
Дайте определения асимптот графика функции.
Практическое занятие по теме: Числовые ряды
Цель: Научиться работать с числовыми рядами в системе MathCAD.
Основные понятия. Ряды с неотрицательными членами
Рассмотрим произвольную числовую последовательность {un}. Составленное выражение
![]()
называют числовым рядом или просто рядом. Члены последовательности {un} называют членами ряда. Сумма первых n членов ряда
![]()
называется n-й частичной суммой ряда.
Ряд называется сходящимся, если существует и конечен предел последовательности {Sn} частичных сумм этого ряда. При этом предел последовательности частичных сумм называется суммой ряда.
Обозначаем
![]()
![]() или
или
![]()
Если предел
последовательности частичных сумм не
существует или бесконечен, то ряд
расходится.
Справедливо следующее утверждение. Для
того чтобы ряд
![]() сходился, необходимо, чтобы последовательность
его членов {un}
стремилась к нулю при n → .
Другими словами, если ряд сходится, то
его члены стремятся к нулю на бесконечности.
Обратное, вообще говоря, неверно. Члены
ряда могут стремиться к нулю, но ряд при
этом расходится.
сходился, необходимо, чтобы последовательность
его членов {un}
стремилась к нулю при n → .
Другими словами, если ряд сходится, то
его члены стремятся к нулю на бесконечности.
Обратное, вообще говоря, неверно. Члены
ряда могут стремиться к нулю, но ряд при
этом расходится.
Ниже приведен фрагмент рабочего документа MathCAD, содержащий исследование расходящегося и сходящегося рядов; для каждого исследуемого ряда построен график последовательности частичных сумм и членов ряда.
![]()
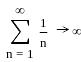 Ряд
расходится
Ряд
расходится
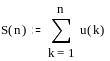
![]()
![]()
![]()
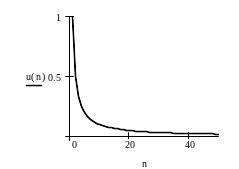
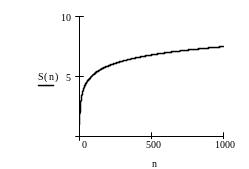
Ряд Лейбница
![]()
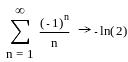 Ряд
сходится
Ряд
сходится
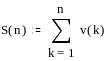
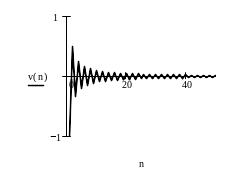
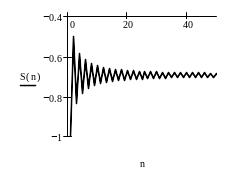
Замечание.
Для того чтобы вычислить символьно
сумму ряда, щелкните по кнопке
![]() в панели
в панели
![]() ,
введите с клавиатуры в помеченных
позициях переменную суммирования и
границы ее изменения, введите имя или
выражение для члена ряда, как функции
переменной n,
выделите ряд рамкой, щелкните по клавишам
<Ctrl> + <ю>
и по рабочему документу вне выделяющей
рамки.
,
введите с клавиатуры в помеченных
позициях переменную суммирования и
границы ее изменения, введите имя или
выражение для члена ряда, как функции
переменной n,
выделите ряд рамкой, щелкните по клавишам
<Ctrl> + <ю>
и по рабочему документу вне выделяющей
рамки.
В приведенном
фрагменте исследована сходимость двух
часто встречающихся рядов – расходящегося
ряда
![]() который называется гармоническим
рядом, и
сходящегося ряда
который называется гармоническим
рядом, и
сходящегося ряда
![]() называемого рядом
Лейбница.
Другие часто встречающиеся ряды –
обобщенный
гармонический ряд
называемого рядом
Лейбница.
Другие часто встречающиеся ряды –
обобщенный
гармонический ряд
![]() который сходится при
который сходится при
![]() и расходится при
и расходится при
![]() ,
и ряд типа
прогрессии
,
и ряд типа
прогрессии
![]() который сходится при
который сходится при
![]() и расходится при
и расходится при
![]()
Исследовать на сходимость числовые ряды с неотрицательными членами можно, используя теоремы сравнения и признаки сходимости.
Рассмотрим два числовых ряда с неотрицательными членами
 и
и

 Если при всех n,
начиная с некоторого, справедливо
неравенство
Если при всех n,
начиная с некоторого, справедливо
неравенство
 то из сходимости ряда
следует сходимость ряда
то из сходимости ряда
следует сходимость ряда
 и наоборот, из расходимости ряда
и наоборот, из расходимости ряда
 следует расходимость ряда
следует расходимость ряда

Рассмотрим два числовых ряда с неотрицательными членами и Если
 то ряды
и
сходятся или расходятся одновременно.
то ряды
и
сходятся или расходятся одновременно.
При использовании теорем сравнения исследуемый ряд чаще всего сравнивают с простейшими рядами – с обобщенным гармоническим или с рядом типа прогрессии.
Признак
сходимости Даламбера.
Для ряда с положительными членами
![]()
![]() вычислим предел
вычислим предел
![]() Если
Если
![]() то ряд
сходится, если
то ряд
сходится, если
![]() – расходится. При
– расходится. При
![]() вопрос о сходимости ряда остается
открытым: ряд может оказаться как
сходящимся, так и расходящимся.
вопрос о сходимости ряда остается
открытым: ряд может оказаться как
сходящимся, так и расходящимся.
Признак
сходимости Коши.
Для ряда с положительными членами
вычислим предел
![]() Если
Если
![]() то ряд
сходится, если
то ряд
сходится, если
![]() – расходится. При
– расходится. При
![]() вопрос о сходимости ряда остается
открытым: ряд может оказаться как
сходящимся, так и расходящимся.
вопрос о сходимости ряда остается
открытым: ряд может оказаться как
сходящимся, так и расходящимся.
Ниже приведен фрагмент рабочего документа MathCAD, содержащий исследование рядов с использованием обоих признаков сходимости.
![]()
![]() Ряд
сходится
Ряд
сходится
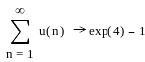
![]()
![]() Ряд
сходится
Ряд
сходится
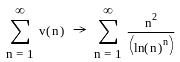 Сумма
ряда символьно не вычисляется
Сумма
ряда символьно не вычисляется
ЗАДАНИЕ 1.
Исследуйте на сходимость числовые ряды
![]() ,
,
![]() .
.
Порядок выполнения задания
Определите члены исследуемых рядов как функции переменной n.
Определите частичные суммы рядов как функции переменной n.
Вычислите пределы членов ряда и частичных сумм при n → .
Постройте графики членов ряда и частичных сумм как функций переменной n.
Фрагмент рабочего документа MathCAD с соответствующими вычислениями приведен ниже.
![]()
![]()
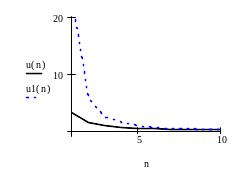
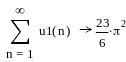
Ряд
![]() сходится. По первой теореме сравнения
ряд
сходится. По первой теореме сравнения
ряд
![]() сходится.
сходится.
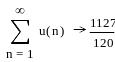
![]()
![]()
![]()
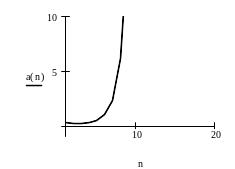
По
признаку Даламбера ряд
![]() расходится.
расходится.

