Исследование функции с помощью производной

Если функция дифференцируема на промежутке (a, b), за исключением, может быть, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум, используя следующие утверждения.

Для того чтобы дифференцируемая на (a, b) функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы ( ) на (a, b).

Пусть в точке x = x₀ производная Если существует окрестность точки x₀ такая, что в этой окрестности при x < x₀ и при x > x₀, то функция имеет в точке x₀ максимум. Если же при x < x₀ и при x > x₀, то функция имеет в точке x₀ минимум.

Если непрерывная в точке x₀ функция f(x) дифференцируема на при этом на (a, x₀) и на (x₀, b), то функция имеет в точке x₀ максимум; если же на (a, x₀) и на (x₀, b), то функция имеет в точке x₀ минимум.

ЗАДАНИЕ 2. Изобразите график заданной функции и подтвердите построение аналитическим исследованием: постройте график производной, найдите нули производной. Найдите координаты точек экстремума.

Порядок выполнения задания

1. Определите функцию f(x) и постройте ее график.

2. Постройте график производной.

3. Найдите нули производной, решив уравнение

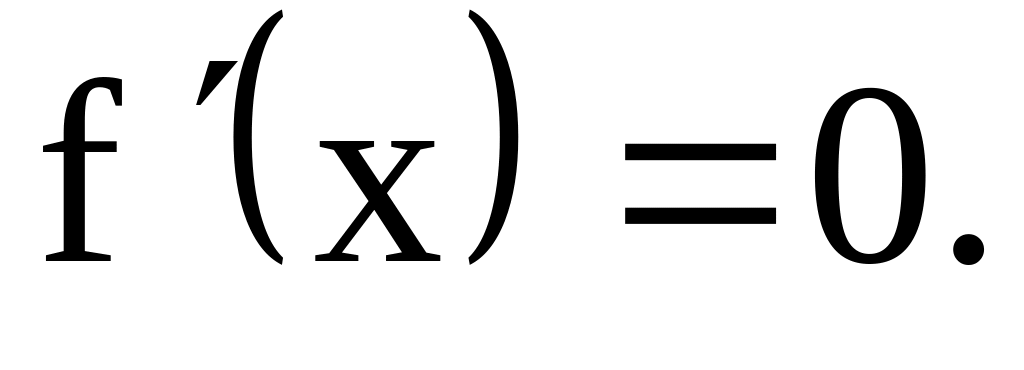
4. Вычислите и запишите координаты точек экстремума. Укажите их тип (максимум / минимум).

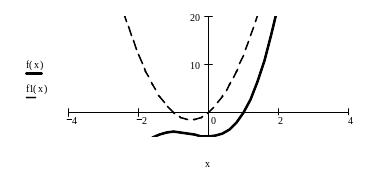
Пример выполнения задания для функции с соответствующими вычислениями и графиками приведен ниже.

_{Точка максимума (-1, -4)}

_{Точка минимума (0, -5)}

Исследование функции с использованием второй производной

Если функция дважды дифференцируема на промежутке (a, b), за исключением, может быть конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости или вогнутости.

График функции f(x) называется выпуклым (выпуклым вниз) на промежутке (a, b), если он расположен выше касательной, проведенной в любой точке (x, f(x)), x  (a, b). Если же график функции лежит ниже касательной, то он называется вогнутым (выпуклым вверх).

Справедливо следующее утверждение. Если дважды дифференцируемая на промежутке (a, b) функция f(x) имеет на нем положительную вторую производную, то функция выпукла на (a, b). Если же вторая производная отрицательна на промежутке (a, b), то функция на нем вогнута.

Если вторая производная равна нулю в точке x = x₀, а слева и справа от нее имеет значения разных знаков, то точка x = x₀ – точка перегиба.

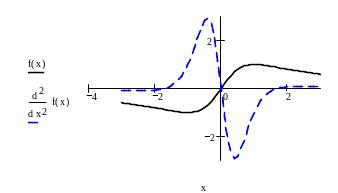
На рис. 8 представлен график функции с тремя точками перегиба, на примере функции .

ЗАДАНИЕ 3. Изобразите график заданной функции и подтвердите построение аналитическим исследованием: постройте график второй производной, найдите нули второй производной. Найдите координаты точек перегиба.

Порядок выполнения задания

1. Определите функцию f(x) и постройте ее график.

2. Постройте график второй производной.

3. Найдите нули второй производной, решив уравнение

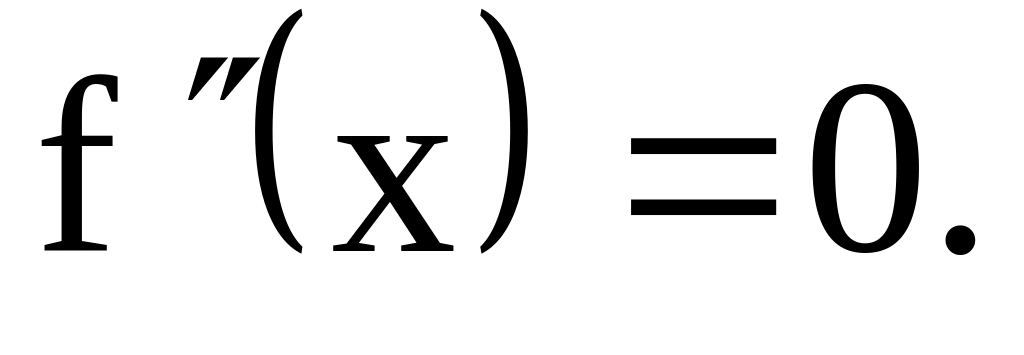
4. Вычислите и запишите координаты точек перегиба.

5. Опишите интервалы выпуклости и вогнутости функции.

Пример выполнения задания для функции с соответствующими вычислениями и графиками приведен ниже.

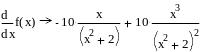
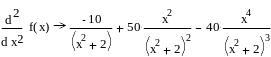
Упрощенное выражение

Упрощенное выражение :

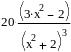
Точка максимума: (0, 0)

Точки перегиба соответствуют равенству 3x² – 2 = 0, т.е. .