Сеть Вольтерри

1. Число нейронов – потомков у каждого нейрона сети Вольтерри зависит от – числа единичного задержания

2. По формуле: 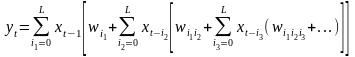рассчитывается выходное значение сети:Вольтерри

3. Сеть Вольтеррн обучается при помощи … алгоритмов обучения Градиентных

4. По формуте 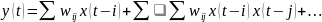рассчитываются выходные значения сети ВОЛЬТЕРРИ

5. Сеть Вольтерри относится к сетям следующего типа прямого распределения сигнала

Теория нечетких множеств

1. Логическое произведение нечетких множеств А и В определяется как min[A(e)(x)]

2. Формирование значения импликации правила «если х1 – это А1 и х2 – это А2 и хn – это Аn, y – это В» называется – агрегирование на уровне импликации

3. Дефуззификатор трансформирует нечетное множество в полностью … решение y – четкое

4. Формула 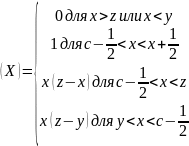описывает функцию фузификации - трапециидальную

5. Функция T(S(w1,x1),S(w2,x2),…,S(sn,xn)) реализована на входе нечеткого нейрона типа – N

6. Агрегация равнозначных результатов импликации многих правил чаще всего реализуется при помощи операции …Логической или алгебраической суммы

7. Наиболее распространёнными функциями принадлежности, используемыми для фуззификации, являются: Гаусса, Треугольная, Трапецеидальная

8. Функция 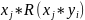реализована на выходе нечёткого нейрона: Композиция правил

9. Ограниченное произведение нечётких множеств A и B определяется как

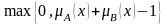
10. Для агрегирования условия правила «если – то» наиболее часто используются операции …Алгебраическое произведение или логическое

11. Функция s(t(w,x),t(w,x),…,f(w,x)) реализованная на выходе нечёткого нейрона типа …ИЛИ

12. Гибридная нейронная нечёткая сеть Абе и Лэна состоит изБолее 3х слоёв

13. Логическая сумма нечетких множеств А и В определяется так: Max(A(x), B(x))

14. Для агрегирования результата импликаций правил «если-то» в системах нечеткого вывода наиболее часто используется операция MAX

15. Фуззификатор преобразует N-мерный входной вектор x=[x₁,x₂,…,x_n] в НЕЧЕТКОЕ множество А, характеризуемое функцией принадлежности m(x) с НЕЧЕТКИМИ переменными.

16. Функция s(t(w,x),t(w,x)…t(w,x)) реализована на выходе нечеткой нейрона типа ИЛИ

17. Алгоритм С-means предназначена для обучения НЕЧЕТКИХ НЕЙРОННЫХ СЕТЕЙ

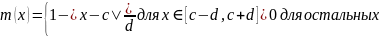18. Формула описывает ТРЕУГОЛЬНУЮ функцию фуззификации.

Сеть Мамдани-Заде

1. Правило вида «Если X₁ – это A₁ и X₂ – это A₂ и X_N – это A_N, то Y – это B», отображает модель Мамдани-Заде

2. Если в качестве агрегатора в правилах использовать оператор алгебраического произведения, а деффузификацию реализовать относительно среднего центра, то сеть Ванга-Менделя реализует модель нечеткого вывода: МАМДАНИ-ЗАДЕ

Сеть Такаги-Сугено-Канга

1. Правила вида «если если х1 – это А1 и х2 – это А2 и хn – это Аn, то 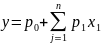» отображает модель – Такаги-Сугено-Канга

2. Правило вида «если х₁ – это А₁ и х₂ – A₂ и х_n – A_n», то y=f(х₁, х₂, …,х_n) отображает общую формулу модели :ТАКАГИ-СУГЕНО-КАНГА

3. Гибридный алгоритм обучения нечетких сетей может применяться для сетей ВАНГА-МЕНДЕЛЯ И TSK

Сеть Цукамото

1. Модель нечеткого вывода Цукамото реализует – гибридный нейронечеткий классификатор

2. По формул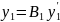е где 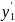есть 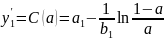рассчитывается выходное значение нечеткой сети - гибриднонейронечеткого классификатора

3. Правило вида «если Х₁ – это А₁ и Х₂ – это А₂ и Х_N – это А_N, то Y = f^-1(W)» где W – уровень срабатывания предпосылки правила, отображает модель Цукамото

4. По формуле 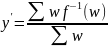формируется выходной сигнал в модели нечеткого вывода ЦУКАМОТО

5. Для обучения гибритногонейронечёткого классификатора используется … алгоритмы Градиентные