3.3 Определение избыточной работы внешних сил

График работы сил сопротивления строим путем графического интегрирования графика приведенного момента сил.

Рассматриваем установившейся режим движения механизма, тогда работа движущих сил за цикл равна работе сил сопротивления,

.

В первом приближении считаем момент движущих сил М_дв постоянным, тогда графиком работы движущих сил А_дв будет прямая, соединяющая начало (точку 0) и конец (точку 12) графика А_с(₁). Построенный график работы движущих сил А_дв получился с отрицательным знаком в масштабе:

,

где Н=100 мм - полюсное расстояние.

Для получения графика приведенного момента движущих сил продифференцируем график работы движущих сил . Для этого, из полюса графика , проведем луч параллельно графику –А_дв до пересечения с осью ординат. Из полученной точки пересечения проводим горизонтальную прямую, которая и будет графиком .

Для получения графика избыточной работы А внешних сил, мы графи чески вычитаем из графика работы движущих сил график работы А_с(₁) сил сопротивления.

А=А_дв-А_с

Масштаб этого графика оставляем равным масштабу графика работы движущих сил и сил сопротивления.

4 Проектирование редуктора

4.1 Выбор электродвигателя и кинематический расчет

Из графика определяем движущий момент на валу кривошипа

Нм,

где y_M=56,6 мм - ордината графика .

Требуемая мощность электродвигателя

кВт,

где  - общий КПД редуктора, который находим как произведение КПД всех элементов привода.

Выбираем из справочника необходимые для расчетов КПД:

КПД ступени закрытого зубчатого редуктора (цилиндрической)

КПД ременной передачи

КПД подшипников качения (одна пара)

Выбираем асинхронный двигатель марки 4А132S6У3, имеющий мощность частоту вращения вала двигателя Угловая скорость на валу электродвигателя

Требуемое передаточное число привода можно определить по формуле:

С учетом кинематической схемы привода разбиваем по отдельным ступеням:

,

где - передаточное число редуктора;

- передаточное число ременной передачи;

Примем ориентировочно . Тогда зная общее передаточное число привода и принятое нами передаточное число ременной передачи, найдем ориентировочное значение передаточного числа редуктора:

Передаточное число редуктора выбираем из стандартного ряда .

Уточняем передаточное число ременной передачи

Определяем мощности, крутящие моменты, угловые скорости и частоты вращения для всех валов привода по формулам:

где i = 1…3 – номер вала привода.

Полученные значения сводим в таблицу 1.

Таблица 4.1

№ вала
1	4,22	970	101,6	0,0415
2	3,99	324,7	34	0,117
3	3,85	81,17	8,5	0,453

4.2 Расчет зубчатой передачи

4.2.1 Выбор материала и допускаемых напряжений для шестерни и колеса. Выбираем материал для шестерни и колеса – Сталь 40Х (поковка); термообработка – нормализация.

Для шестерни:

Твердость ; предел прочности предел текучести

Для колеса:

Твердость ; предел прочно предел текучести

4.2.2 Определяем допускаемое напряжение изгиба для шестерни по формуле:

Предварительно находим предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений:

где предел выносливости зубьев шестерни при изгибе, соответствующий базовому числу перемен напряжений. коэффициент, учитывающий влияние двухстороннего приложения нагрузки при одностороннем приложении нагрузки

коэффициент долговечности

Здесь показатель степени кривой выносливости при изгибе: при базовое число циклов перемены напряжений эквивалентное число циклов перемены напряжений

Так как то принимаем соответственно

Коэффициент безопасности где коэффициент, учитывающий нестабильность характеристики материала, коэффициент, учитывающий способ получения заготовки и условия эксплуатации передачи,

Коэффициент учитывает чувствительность материала к концентрации напряжений в функции от модуля зацепления. При проектировочном расчете ввиду неопределенности модуля Коэффициент учитывает шероховатость переходной поверхности зуба в зависимости от способа обработки. Принимаем

Находим допускаемые напряжения изгиба для зуба шестерни:

4.2.3 Допускаемое напряжение изгиба для зуба колеса:

Предварительно находим предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений:

где предел выносливости зубьев колеса при изгибе, соответствующий базовому числу перемен напряжений.

коэффициент, учитывающий влияние двухстороннего приложения нагрузки при одностороннем приложении нагрузки

коэффициент долговечности

При базовое число циклов перемены напряжений эквивалентное число циклов перемены напряжений:

Так как то принимаем соответственно

Находим допускаемые напряжения изгиба для зуба колеса

4.2.4 Определяем допускаемое напряжение изгиба при расчете на действие максимальной нагрузки для зуба шестерни по формуле:

где предельное напряжение, не вызывающее остаточных деформаций или хрупкого излома зуба шестерни.

определяется так же, как и при расчете на выносливость при изгибе. коэффициент безопасности, , где

Следовательно,

4.2.5 Допускаемое напряжение изгиба при расчете на действие максимальной нагрузки для зуба колеса:

где предельное напряжение, не вызывающее остаточных деформаций или хрупкого излома зуба колеса.

коэффициент безопасности, , где

Следовательно,

4.2.6 Определяем допускаемое напряжение на контактную выносливость для зуба шестерни по формуле:

где предел контактной выносливости поверхности зубьев шестерни, соответствующий эквивалентному числу циклов перемен напряжений:

Коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки передачи рассчитываем по формуле:

где базовое число циклов перемен напряжений эквивалентное (суммарное) число циклов перемены напряжений:

Отношение поэтому коэффициент долговечности определяем по формуле: т. е. принимаем

Предел контактной выносливости:

Коэффициент безопасности для зубьев с однородной структурой материала . Коэффициент , учитывающий шероховатость сопряженных поверхностей зубьев, выбираем . Коэффициент учитывающий окружную скорость, в предварительных расчетах принимают

Получаем:

4.2.7 Допускаемые контактные напряжения для зуба колеса:

где придел контактной выносливости поверхности зубьев колеса, соответствующий эквивалентному числу циклов перемен напряжений:

Коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки передачи рассчитываем по формуле:

где базовое число циклов перемен напряжений эквивалентное (суммарное) число циклов перемены напряжений:

Отношение поэтому коэффициент долговечности определяем по формуле:

т. е.

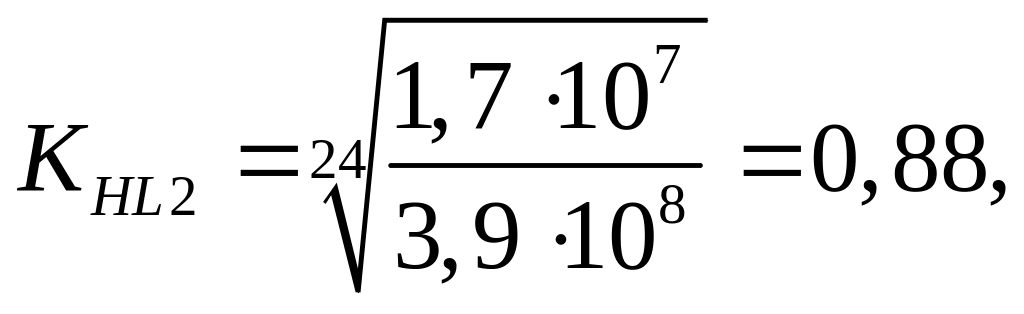
принимаем Предел контактной выносливости:

Коэффициент безопасности для зубьев с однородной структурой материала . Коэффициент , учитывающий шероховатость сопряженных поверхностей зубьев, выбираем . Коэффициент учитывающий окружную скорость, в предварительных расчетах принимают .

Получаем:

4.2.8 Определяем допускаемое контактное напряжение передачи:

Проверяем выполнение условия . Условие выполняется.

4.2.9 Находим допускаемое контактное напряжение при расчете на действие максимальной нагрузки для зуба шестерни по формуле:

для зуба колеса:

4.2.10 Расчет передачи на контактную выносливость. Вычислим начальный диаметр шестерни:

Предварительно определяем величины, необходимые для расчета.

Номинальный крутящий момент на шестерне находится по формуле:

где номинальная мощность, передаваемая шестерней, частота вращения шестерни, тогда

Ориентировочная окружная скорость колес находится по формуле:

При данной скорости требуется степень точности передачи – 9-я.

Коэффициент, учитывающий распределение нагрузки между зубьями

Максимальное значение коэффициента ширены зубчатого венца при не симметричном расположении шестерни:

Определяем значение коэффициента ширены зубчатого венца:

,

где коэффициент К=3, угол наклона зубьев принимаем , расчетное число зубьев шестерни .

Коэффициент, учитывающий динамическую нагрузку (определяем интерполированием).

Коэффициент, учитывающий распределение нагрузки по ширине венца определяем по графику в зависимости от коэффициента

Коэффициент, учитывающий форму сопряженных поверхностей:

.

Коэффициент, учитывающий механические свойства материала зубчатых колес для стальных колес.

Число зубьев колеса Принимаем

Коэффициент торцевого перекрытия который находится по формуле:

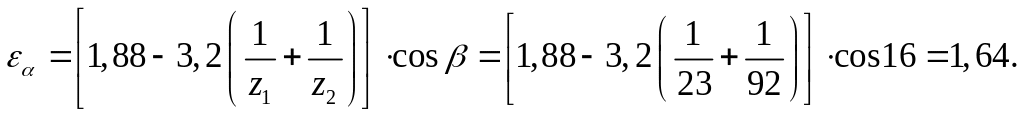
Коэффициент, учитывающий суммарную длину контактных линий , который находится по формуле:

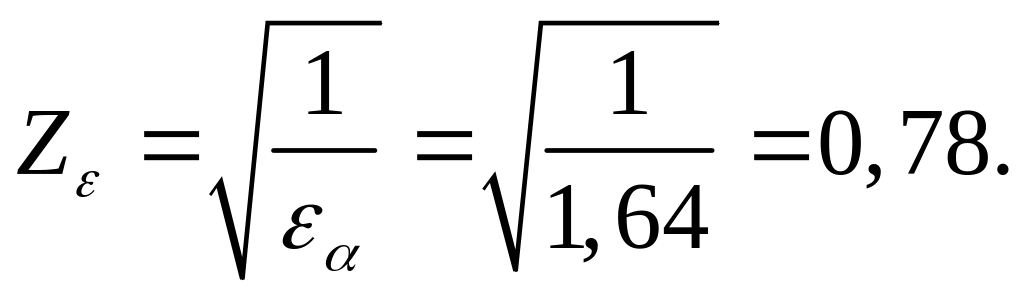
Начальный диаметр шестерни:

Модуль зацепления:

Полученный модуль округляем до стандартного значения По стандартному модулю пересчитываем начальный диаметр:

4.2.11 Проверочный расчет передачи на контактную выносливость.

Определим расчетную окружную скорость при начальном диаметре шестерни

Расчетная окружная скорость колес находится по формуле:

При данной скорости рекомендуемая степень точности передачи – 9-я, что совпадает с ранее принятой степенью точности.

Уточняем начальный диаметр шестерни:

Уточняем по скорости коэффициенты, входящие в формулу.

Коэффициент, учитывающий динамическую нагрузку коэффициент , учитывающий окружную скорость, в предварительных расчетах принимаем

Следовательно:

По уточненному начальному диаметру находим модуль зацепления:

Полученный модуль вновь округляем до стандартного значения , что совпадает с ранее принятой величиной модуля; следовательно, диаметр начальной окружности шестерни

Ширина зубчатого венца при принимаем

4.2.12 Проверочный расчет зубьев на контактную прочность при действии максимальной нагрузки

Расчетное напряжение, создаваемое максимальной нагрузкой определяется по формуле:

,

где действующее напряжение при расчете на контактную выносливость:

Расчетное контактное напряжение от максимальной нагрузки:

где задано в исходных данных расчета.

4.2.13 Проверочный расчет зубьев на выносливость по напряжениям изгиба. Вычисляем напряжение изгиба в зубьях шестерни:

Предварительно определяем эквивалентное число зубьев шестерни и колеса:

Коэффициенты формы зуба для шестерни и колеса соответственно Коэффициент, учитывающий влияние наклона зуба на напряженное состояние

Удельную расчетную нагрузку определяем по формуле:

коэффициент, учитывающий распределение нагрузки между зубьями, коэффициент, учитывающий распределение нагрузки по ширине венца при не симметричном расположении зубчатого колеса , определяем по графику в зависимости от коэффициента коэффициент, учитывающий динамическую нагрузку (определяется интерполированием).

соответственно

Вычисляем напряжение изгиба в зубьях колеса:

4.2.14 Проверочный расчет зубьев на прочность при изгибе максимальной нагрузкой. Расчетное напряжение изгиба от максимальной нагрузки находится по формуле:

Напряжение изгиба от максимальной нагрузки в зубьях шестерни находится по формуле:

в зубьях колеса:

где задано в исходных данных.

4.2.15 Окончательно принимаем параметры передачи:

Определяем делительный диаметр колеса:

Определяем межосевое расстояние первой ступени:

4.2.16 Округляем межосевое расстояние до стандартного числа и пересчитываем угол наклона зуба, делительные диаметры шестерни и колеса:

Проверяем межосевое расстояние: