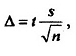Расчетная работа по теории вероятностей Николаевой Н.А. гр.622, 15 вариант.
Задание 2.
СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
39,3 |
37,4 |
36,8 |
32,7 |
23,1 |
20,6 |
24,1 |
42,8 |
27 |
42,2 |
49,7 |
30,9 |
24,5 |
43,7 |
47,9 |
27,1 |
23,7 |
34,1 |
34,4 |
36,3 |
37,2 |
35,8 |
52,8 |
59,1 |
31,8 |
54,3 |
54,7 |
44,9 |
29,8 |
50,2 |
28,8 |
34,6 |
37,2 |
37,3 |
45,9 |
38,7 |
42,7 |
33,3 |
34,5 |
44,8 |
40,4 |
48,2 |
44,8 |
29,6 |
62,8 |
37 |
30,5 |
53,1 |
45,5 |
37,8 |
32,2 |
43,1 |
39,8 |
44,6 |
38,6 |
47,9 |
34,8 |
45,3 |
50,1 |
51,9 |
35,7 |
43,7 |
37,5 |
28 |
45,5 |
31,5 |
35,6 |
31,1 |
42 |
39,8 |
59,3 |
45,5 |
56,9 |
24,3 |
44,2 |
46,7 |
51,6 |
43,1 |
47 |
48,5 |
63,4 |
53,3 |
41 |
26,4 |
46,4 |
65,7 |
22,2 |
34,8 |
33,2 |
46,7 |
39,7 |
24,6 |
51,7 |
34 |
46,4 |
35,6 |
55,1 |
65,7 |
48 |
51,1 |
20,6 |
34,1 |
40,4 |
47,9 |
22,2 |
34,4 |
41 |
47,9 |
23,1 |
34,5 |
42 |
48 |
23,7 |
34,6 |
42,2 |
48,2 |
24,1 |
34,8 |
42,7 |
48,5 |
24,3 |
34,8 |
42,8 |
49,7 |
24,5 |
35,6 |
43,1 |
50,1 |
24,6 |
35,6 |
43,1 |
50,2 |
26,4 |
35,7 |
43,7 |
51,1 |
27 |
35,8 |
43,7 |
51,6 |
27,1 |
36,3 |
44,2 |
51,7 |
28 |
36,8 |
44,6 |
51,9 |
28,8 |
37 |
44,8 |
52,8 |
29,6 |
37,2 |
44,8 |
53,1 |
29,8 |
37,2 |
44,9 |
53,3 |
30,5 |
37,3 |
45,3 |
54,3 |
30,9 |
37,4 |
45,5 |
54,7 |
31,1 |
37,5 |
45,5 |
55,1 |
31,5 |
37,8 |
45,5 |
56,9 |
31,8 |
38,6 |
45,9 |
59,1 |
32,2 |
38,7 |
46,4 |
59,3 |
32,7 |
39,3 |
46,4 |
62,8 |
33,2 |
39,7 |
46,7 |
63,4 |
33,3 |
39,8 |
46,7 |
65,7 |
34 |
39,8 |
47 |
65,7 |
Исходный и упорядоченный вариационные ряды
1)Проведем простейшую статистическую обработку
Размах R=xmax-xmin= |
45,1 |
Количество разрядов(интервалов) k=1+3,32*lg(n)= |
8 |
Длина интервала Δx=R/k= |
6 |
Построим интервальную таблицу частот
Границы интервалов |
Среднее значение x̄i |
Частота mi |
Относит.частота wi=mi/n |
Высота столбца гистограммы h= wi/ Δx |
20-26 |
23 |
8 |
0,08 |
0,0133 |
26-32 |
29 |
12 |
0,12 |
0,0200 |
32-38 |
35 |
24 |
0,24 |
0,0400 |
38-44 |
41 |
16 |
0,16 |
0,0267 |
44-50 |
47 |
21 |
0,21 |
0,0350 |
50-56 |
53 |
12 |
0,12 |
0,0200 |
56-62 |
59 |
3 |
0,03 |
0,0050 |
62-68 |
65 |
4 |
0,04 |
0,0067 |
2) Вычислим числовые характеристики
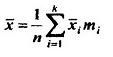
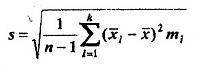
Медиана x̃= |
40,1 |
|
|
Выборочное среднее x̄= |
40,88 |
s^2= |
|
Стандартное отклонение s= |
10,51 |
3) Построим доверительный интервал для мат.Ожидания
|
Доверительная вероятность γ= |
0,9545 |
|
Значение функции Лапласа (из приложения) Ф(t)= |
0,47725 |
|
t= |
2 |
|
Предельная ошибка Δ= |
2,103 |
|
|
|
|
Дов. интервал для мат.ожидания |
(37,997; |
42,983) |
4)Проведем аппроксимацию гистограммы нормальным законом распределения
Среднее значение x̄i |
ui=(x̄i-x̄)/s |
ϕ(ui) |
f(x̄i)=1/s*ϕ(ui) |
23 |
-1,70 |
0,0925 |
0,0088 |
29 |
-1,13 |
0,2107 |
0,0200 |
35 |
-0,56 |
0,341 |
0,0324 |
41 |
0,01 |
0,3989 |
0,0379 |
47 |
0,58 |
0,3372 |
0,0321 |
53 |
1,15 |
0,2036 |
0,0194 |
59 |
1,72 |
0,0893 |
0,0085 |
65 |
2,29 |
0,0283 |
0,0027 |
Построим график теоретической кривой и гистограмму
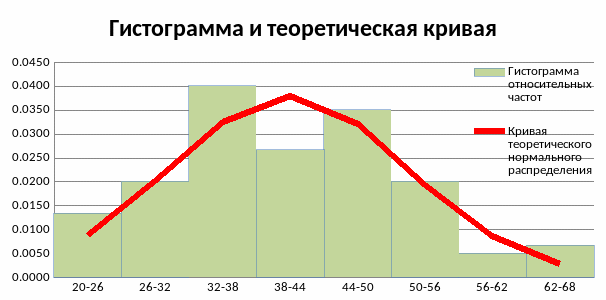
5 )Проверим согласованность статического и теоретического распределений
Вычислим статистику
|
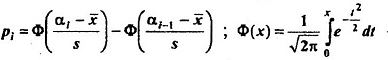
Число степеней свободы r=k-3= |
5 |
|
|
Уровень значимости = 0,05 |
χ^2кр(5;0,05)=11,1 |
|
Границы интервалов |
Частота mi |
|
|
||||
20-26 |
7 |
0,055 |
0,411 |
||||
26-32 |
13 |
0,121 |
0,072 |
||||
32-38 |
24 |
0,193 |
1,149 |
||||
38-44 |
16 |
0,225 |
1,859 |
||||
44-50 |
21 |
0,190 |
0,200 |
||||
50-56 |
12 |
0,118 |
0,005 |
||||
56-62 |
3 |
0,053 |
0,993 |
||||
|
χ^2= |
7,654 |
|
|
|
||
Вывод: χ^2< χ^2кр => можно принять гипотезу о нормальном распределении, т.е. полученный теоретический закон хорошо аппроксимирует статическое распределение.
Задание 3.
ЭЛЕМЕНТЫ КОРЕЛЛЯЦИОНОГО АНАЛИЗА
Исходные данные
39,3 |
215,7 |
37,4 |
205,9 |
36,8 |
199,6 |
32,7 |
175,8 |
23,1 |
130,6 |
20,6 |
109 |
26,1 |
125,4 |
42,8 |
220,6 |
27 |
138 |
42,2 |
217,7 |
49,7 |
255 |
30,9 |
176,6 |
24,5 |
142,5 |
43,7 |
223,7 |
47,9 |
251,4 |
27,1 |
145,4 |
23,7 |
125,5 |
34,1 |
181,5 |
34,4 |
189,7 |
36,3 |
193,6 |
37,2 |
208,9 |
35,8 |
188,9 |
52,8 |
269,7 |
59,1 |
299,8 |
31,8 |
181,5 |
54,3 |
287,8 |
54,7 |
282 |
44,9 |
244,6 |
29,8 |
164,9 |
50,2 |
270,1 |
28,8 |
165,9 |
34,6 |
185,9 |
37,2 |
201,7 |
37,3 |
197,5 |
45,9 |
241,8 |
38,7 |
199,4 |
42,7 |
217,9 |
33,3 |
187,9 |
34,5 |
181,2 |
44,8 |
241 |
40,4 |
212,2 |
48,2 |
263,6 |
44,8 |
246,5 |
29,6 |
151,4 |
62,8 |
331,8 |
37 |
200,9 |
30,5 |
162,3 |
53,1 |
274,4 |
45,5 |
240,4 |
37,8 |
202,4 |
32,2 |
170,3 |
43,1 |
223,8 |
39,8 |
213,8 |
44,6 |
235,8 |
38,6 |
215,6 |
47,9 |
258,9 |
34,8 |
183,9 |
45,3 |
247,4 |
50,1 |
272 |
51,9 |
273,1 |
35,7 |
183 |
43,7 |
236,4 |
37,5 |
201,9 |
28 |
154,9 |
45,5 |
230,8 |
31,5 |
172,7 |
35,6 |
190,4 |
31,1 |
175,5 |
42 |
215,1 |
39,8 |
217,4 |
59,3 |
306,8 |
45,5 |
235,1 |
56,9 |
306,8 |
24,3 |
140,6 |
44,2 |
237,2 |
46,7 |
246,2 |
51,6 |
276,2 |
43,1 |
223,1 |
47 |
257,7 |
48,5 |
256,1 |
63,4 |
326,4 |
53,3 |
277,8 |
41 |
211,7 |
26,4 |
147,2 |
46,4 |
250,8 |
65,7 |
341,4 |
22,2 |
125,1 |
34,8 |
178,4 |
33,2 |
170,5 |
46,7 |
241,2 |
39,7 |
202,5 |
24,6 |
131 |
51,7 |
262,9 |
34 |
173,1 |
46,4 |
249 |
35,6 |
190,3 |
55,1 |
282,4 |
65,7 |
335,4 |
48 |
248,4 |
51,1 |
260,4 |