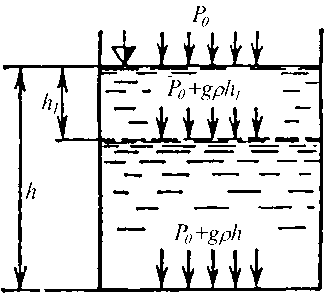
Поверхность равного давления . Виды поверхности равного давления

Поверхность, все точки которой испытывают одинаковое давле­ние, называются поверхностью равного давления. Анализируя основ­ное уравнение гидростатики можнозаключить, что поверхностя­ми равного давления в объеме покоящейся относительно земли жид­кости являются горизонтальные плоскости (при p = const будет и z = const

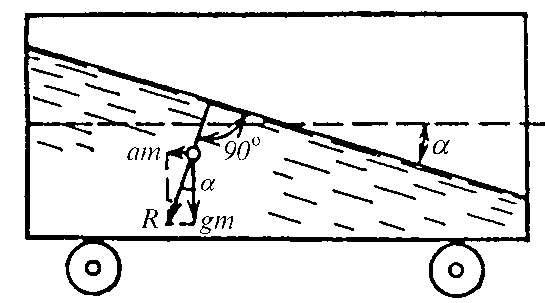
Рис.1.9. Поверхность равного давления при действии силы тяжести

Последовательное соединение трубопроводов

Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).

Рис. 6.3. Последовательное соединение трубопроводов

При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:

Q₁ = Q₂ = Q₃ = Q

Σ^h_M-N ⁼ Σ^h₁ ⁺ Σ^h₂ ⁺ Σ^h₃

Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.

Потери напора по длине и в местных сопротивлениях.

Потери напора при движении жидкости вызываются сопротивлениями двух видов: сопротивлениями по длине, определяемыми силами трения, и местными сопротивлениями, обусловленными изменениями скорости потока по направлению и величине.

Местные потери энергии обусловлены так называемыми местными сопротивлениями: местными изменениями формы и размеров русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления, изменяется ее скорость и обычно возникают вихри.

Примерами местных сопротивлений могут служить следующие устройства: задвижка, диафрагма, колено, вентиль.

Местные потери выражаются формулой Вейсбаха.

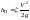
Потери на трение или линейные сопротивления вызываются силами трения, возникающими по всей длине потока жидкости при равномерном движении, поэтому они возрастают пропорционально длине потока. Этот вид потерь обусловлен внутренним трением в жидкости, а поэтому он имеет место не только в шероховатых, но и в гладких трубах.

Потерю напора на трение (по длине) можно определить по формуле:

.

,

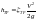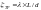Формулу обычно называют формулой Дарси-Вейсбаха

Поток жидкости

Поток жидкости — это часть неразрывно движущейся жидкости, ограниченная твердыми деформируемыми или недеформируемыми стенками, образующими русло потока. Потоки, имеющие свободную поверхность, называются безнапорными(арык, канал). Потоки, не имеющие свободной поверхности, называются напорными.(водопровод,)

Струя- поток жид-ти, ограниченный поверхностями разрыва скоростей, т.е поверхностью в движущейся жид-ти при переходе через которую касательные к этой поверхности векторы скорости скачкообразно изменяют свою величину. (пожарный брандспойт)