М ощность потока

При решении инженерных задач необходимо знать мощность потока. Работа которую может совершить ед массы, объема или силы тяжести, опр – ся полным удельным запасам энергии, давлением и напором, поэтому для получения мощности необходимо умножить на их расходы(массовый, объемный, весовой). Тогда мощность потока:

N_n = ln pQ= p_n Q= H_n pgQ (Вт) н*м/с= дж/с= Вт

Для перемещения вязкой жид – ти необходимо сообщить потоку энергию покрывающую потери напора.

Опыт Рейнольдса.

Существовании двух различных, резко отличающихся режимов движения было известно еще в первой половине XIX века, физиком Рейнольдсом на основе весьма простых и наглядных опытов

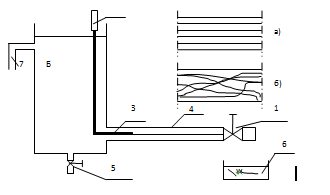
Рейнольдс пропускал жидкость из бака Б, в котором с помощью перелива 7 поддерживался постоянный уровень, через стеклянные трубки различного диаметра, регулируя скорость движения жидкости в них кранами 1 и 5. По тонкой трубке 3 с заостренным концом ко входу в стеклянную трубку 4 подводилась окрашенная жидкость из сосуда 2. Средняя скорость V в трубке 4, имеющей площадь сечения со определялась по объему жидкости W, поступившей в мерный сосуд 6 за время t (рис .).

При малых скоростях течения в потоке жидкости появляются окрашенные струйки. Они движутся прямолинейно, без пульсаций, не перемешиваясь с соседними слоями жидкости (рис. а). (ламинарное).

При постепенном увеличении скорости движения жидкости при некоторой скорости течения параллельно-струйное движение нарушится, окрашенные струйки стали пульсирующими, появятся разрывы. А при дальнейшем увеличении скорости окрашенные струйки исчезнут, перемешавшись с потоком жидкости (рис. 6). (турбулентное).

Рейнольдс установил, что основными факторами, определяющими характер режима, являются: средняя скорость движения жидкости V, внутренний диаметр трубы d, плотность жидкости р, динамическая вязкость µ. Он ввел безразмерный параметр Re, учитывающий влияние перечисленных факторов, называемый числом (или критерием) Рейнольдса.

Re = Vdρ/µ но µ/ρ = ν, тогда .

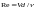В настоящее время считается режим ламинарным при Re < 2320, а турбулентным при Re> 2320.

Параллельное соединение трубопроводов

Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.

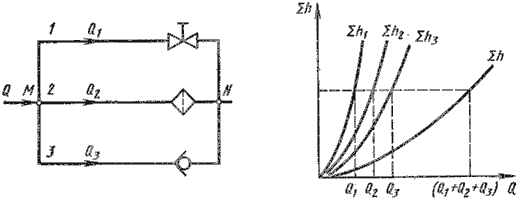
Рис. 6.4. Параллельное соединение трубопроводов

Обозначим полные напоры в точках М и N соответственно H_M и H_N , расход в основной магистрали (т.е. до разветвления и после слияния) - через Q, а в параллельных трубопроводах через Q₁, Q₂ и Q₃; суммарные потери в этих трубопроводах через Σ₁ , Σ₂ и Σ₃.

Очевидно, что расход жидкости в основной магистрали

Q = Q₁ = Q₂ = Q₃

Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :

Σ^h1 ^{= H}_M ^{- H}_N; Σ^h2 ^{= H}_M ^{- H}_N; Σ^h3 ^{= H}_M ^{- H}_N

Отсюда делаем вывод, что

Σ^h₁ ⁼ Σ^h₂ ⁼ Σ^h₃

т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом

Σ^h1 ^{= K}₁Q₁^m; Σ^h2 ^{= K}₂Q₂^m; Σ^h3 ^{= K}₃Q₃^m

где K и m - определяются в зависимости от режима течения.

Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.

Рис. 4.15.

Рис. 4.16. Зависимости ζкол от угла δ

Рис. 4.17. Отвод

6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζ_отв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.

Для отводов круглого сечения с углом δ= 90 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:

Для углов δ 70° коэффициент сопротивления

а при δ 100°

Потеря напора в колене определится как

Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.