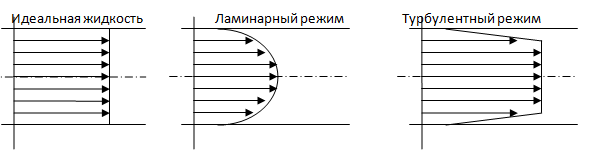
Ламинарный и турбулентный режимы движения жидкости.

Как показали теоретический анализ и опыты при ламинарном режиме движения жидкости в круглой трубе, скорости в поперечном сечении распределены по параболе, скорости у стенок трубы равны нулю и, плавно увеличиваясь, достигают максимума на оси потока. При этом режиме существуют лишь продольные составляющие скоростей. Силы сопротивления движению возникают вследствии трения между слоями жидкости и не зависят от состояния стенок. При турбулентном режиме скорости близки к средней и резко падают в тонком слое у стенок, доходя до нуля. График распределения скоростей вызывается турбулентным перемешиванием в результате поперечных перемешиваний частиц. Быстро движущиеся частицы жидкости из средней части потока сталкиваются с медленно движущимися вблизи стенок, благодаря чему и происходит выравнивание скоростей. И только в поперечном слое, где стенки препятствуют перемешиванию, скорость резко убывает.

Линия тока. Трубка тока. Элементарная струйка и ее св-ва.

Линией тока (рис. 25)называется кривая, проведенная в жидкости, касательные к которой в каждой точке совпадают с направлением векторов скоростей частиц, лежащих в данный момент на этой кривой, причем каждая последующая частица расположена на направлении вектора скорости предыдущей.

Трубкой тока называется трубчатая поверхность, образованная линиями тока, проходящими через все точки конечно малого замкнутого контура, причем все его точки принадлежат различным линиям тока. Жидкость, движущаяся внутри трубки тока, называется элементарной струйкой (элементарная струйка абсолютно непроницаемая).

Элементарная струйка. Если в движущейся жидкости выделить весьма малую элементарную площадку , перпендикулярную направлению течения, и по контуру ее провести линии тока, то полученная поверхность называется трубкой тока, а совокупность линий тока, проходящих сплошь через площадку , образует так называемую элементарную струйку

Элементарная струйка характеризует состояние движения жидкости в данный момент времени t. При установившемся движении элементарная струйка имеет следующие свойства:

1. форма и положение элементарной струйки с течением времени остаются неизменными, так как не изменяются линии тока;

2. приток жидкости в элементарную струйку и отток из нее через боковую поверхность невозможен, так как по контуру элементарной струйки скорости направлены по касательной;

3. скорость и гидродинамическое давление во всех точках поперечного лечения элементарной струйки можно считать одинаковым ввиду малости площади

Манометрическое и вакуумное давление.

. (1.3)

В гидравлических расчётах величину нормального атмосферного давления считают равной =98100 Па.

Из формулы (1.3) видно, что в зависимости от соотношения между и избыточное давление может быть и положительной, и отрицательной величиной. Положительное избыточное давление называют манометрическим, а отрицательное – вакуумметрическим. Приборы, применяемые для измерения + и - , называют соответственно манометрами и вакуумметрами.

По принципу действия манометры и вакуумметры делятся на две группы: жидкостные и механические.

Жидкостный манометр (пьезометр) представляет собой стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединён к точке, где измеряется манометрическое давление.

Манометрическое давление, выраженное через показания манометра, равно:

, (1.4)

где 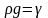- объемный вес жидкости;

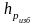- пьезометрическая высота, т.е. высота, отсчитываемая от точки подключения пьезометра до уровня жидкости в нём.

Действие механических приборов основано на деформации под действием давления упругого элемента (пружины или мембраны). Заметим, что пружинный манометр показывает давление в точки жидкости на уровне оси вращения его стрелки. Если высотное положение оси вращения стрелки и точки подключения манометра не совпадает (рис 1.1), в показание манометра ( ) вводят поправку ( ).

1. Когда внутри давление больше атмосферного (p_ст › p_ман), то используются барометр и манометр и тогда

p_ст = p_атм + p_ман ,

где p_ман — давление манометрическое (избыточное).

2. Когда внутри давление меньше атмосферного (p_ст ‹ p_атм), то используются барометр и вакуумметр и тогда

p_ст = p_атм + p_в ,

где p_в — давление вакуумметрическое (см. с. 12).

Эпюры давления

Для расчёта на прочность замкнутых конструкций, ограждающих газ (трубопроводов, баллонов, резервуаров, газгольдеров и т.д.), на их поверхностях строят эпюры давления:

— избыточного p_ман = p_ст – p_атм (рис. 25,а);

— вакуумметрического p_в = p_атм – p_ст (рис. 25,б).

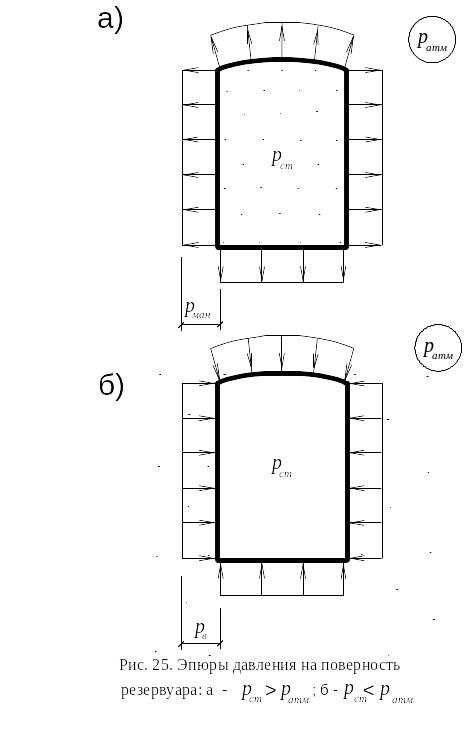
Эпюры давления на рис. 25 построены с пренебрежением изменения давления по высоте резервуара, поэтому на вертикальных стенках они прямоугольные, а не треугольные как для жидкости (см. рис. 5). Такой приём допускается для газа при небольших высотах из-за малости его удельного веса. Эпюры давления служат исходными данными для расчёта конструкций на прочность методами сопромата и строительной механики.

Методы описания движения жидкости.

Для математического описания движения жидкости используются два различных метода (подхода): Лагранжа и Эйлера.

При лагранжевом подходе непрерывный поток жидкости рас-сматривается как движение множества жидких частиц. Для описания перемещения в пространстве отдельной жидкой частицы ее рассматривают как материальную точку, положение которой в данный момент времени t может быть выражено в координатной форме:

x=x(t), y=y(t), z=z(t).                                           (2.1)

В сплошном потоке имеется континуум таких частиц, которые надо как-то выделить (индивидуализировать). Для этого можно в выражение закона движения точки (2.1) добавить в качестве аргументов в общем случае 3 параметра a, b и c – например, значения координат частицы в начальный момент времени. Тогда вместо (2.1) следует записать

x=x(t,a,b,c), y=y(t,a,b,c), z=z(t,a,b,c).                            (2.2)

Параметры  a, b, с называются переменными Лагранжа. Если они фиксированы, то соотношения (2.2) выражают закон движения выделенной жидкой частицы; при изменении этих параметров осуществляется переход от одной частицы к другой и таким образом достигается описание движения всей массы жидкости в целом.

Мгновенная скорость жидкой частицы V может быть представлена своими составляющими в декартовой системе координат

, , .                                      (2.3)

Абсолютная величина (модуль) скорости при этом определяется как .

Другой прием описания движения жидкости, получивший более широкое распространение, был предложен Эйлером. Он основан на понятии местной скорости или скорости в точке. Этим термином обозначают скорость жидкой частицы, находящейся в выбранной точке области течения в данный момент времени. В общем случае местные скорости различны в один и тот же момент времени в различных точках, а также могут изменяться во времени в каждой фиксированной точке. Таким образом, проекции скорости в общем случае могут быть представлены как

u=u(x,y,z,t), v=v(x,y,z,t), w=w(x,y,z,t).                          (2.4)

Этими функциями характеризуется поле скоростей жидкости, т.е. совокупность значений вектора скорости V(u,v,w), определенного в каждой точке области течения. В выражениях (2.3) параметры  x, y, z, t  называются переменными Эйлера.

Ускорение жидкой частицы может быть выражено при комбинации методов Эйлера и Лагранжа:

                     (2.5)

где  – оператор Гамильтона или набла-оператор. В (2.5) вектор  называется локальным ускорением, а вектор – конвективным ускорением.

В скалярной форме составляющие вектора ускорения    по осям декартовой системы координат имеют вид