Уравнение полного давления.

Для двух точек жидкости, одна из которых расположена на сво­бодной поверхности, основное уравнение гидростатики (1.34) записы­вается в виде. p = p₀ + gρ(z-z₀) = p₀ + gρh, где p₀ - давление на свободной поверхности (внешнее давление), z₀ — z = h - глубина погружения т. А.

Из полученного уравнения видно, что давление в жидкости увели­чивается в зависимости от глубины погружения, а формула для определения полного(абсолютного) гидростатического давления в произвольной точке покоящейся жидкости будет p = p₀+gρh.

Уравнение полного напора

Сумма трех высот называется полным напором и обозначается Нg, т.е. полный напор представляет собой сумму пьезометрического Hp=hp+z=P / (r g)+z и скоростного hu=u2/ (2 g) напоров:

С энергетической точки зрения уравнение Бернулли выражает закон сохранения энергии. Полный напор Нg - это полная удельная механическая энергия жидкости в рассматриваемом сечении. Сумма трех членов есть сумма трех удельных энергий: удельной потенциальной энергии давления P / (r g), удельной потенциальной энергии положения z, удельной кинетической энергии u2/ (2 g). Для идеальной жидкости сумма трех удельных энергий (полный напор) по длине струйки есть величина постоянная.

Центр давления жидкости

Для определения положения центра давления воспользуемся известной теоремой статики: момент равнодействующей силы равен сумме моментов сил ее составляющих.

Т.е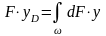 . Из этого выражения можно найти искомую координату центра давления (точки D):

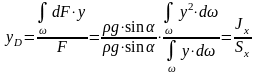,где 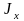- момент инерции площади относительно оси ОХ.

Но момент инерции относительно любой оси может быть выражен через момент инерции относительно центральной оси 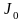(оси, проходящей через центр тяжести фигуры). , где а - расстояние между осями (в нашем случае )

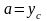Тогда или .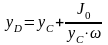

Используя уравнение связи между глубиной h и координатой y, получим уравнение для определения глубины погружения центра давления: .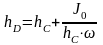

Это выражение показывает, что центр давления лежит всегда ниже центра тяжести (кроме давления на горизонтальную плоскость, когда они совпадают).

Элементы струйной модели

Потоком жидкости называется совокупность элементарных трубок, текущих в заданных границах.

Живым сечением 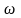называется поверхность , проведенная в границах потока и нормальная ко всем линиям тока (рис.26 ИЛИ Живым сечением потока называется поверхность (поперечное сечение), нормальная ко всем линиям тока, его пересекающим, и лежащая внутри потока жидкости. Площадь живого сечения обозначается буквой ω. Для элементарной струйки жидкости используют понятие живого сечения элементарной струйки (сечение струйки, перпендикулярное линиям тока), площадь которого обозначают через dω. .ед изм - квадратный метр.

<-Живое сечение потока, гидравлический радиус и диаметр, смоченный периметр

Смоченным периметром называется часть периметра живого сечения, соприкасающегося с ограждающими стенками. В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками.

Гидравлический диаметр представляет собой отношение учетверенной площади живого сечения к смоченному периметру

.

Гидравлический радиус - это отношение площади живого сечения к смоченному периметру, он равен 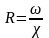и соответственно .

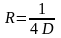При напорном движении в трубе круглого сечения гидравлический радиус будет равен:

,

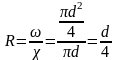т.е. четверти диаметра, или половине радиуса трубы.

Для безнапорного потока прямоугольного сечения с размерами 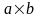гидравлический радиус можно вычислить по формуле

.

Свободная поверхность жидкости при определении смоченного периметра не учитывается.

Количество жидкости, проходящее через живое сечение в единицу времени, называется расходом. Расход может быть объемным, массовым, весовым.

Объемный: ,

Массовый: ,

Весовой: ,

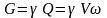где: - средняя скорость,

- площадь живого сечения,

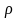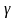- плотность, -удельный вес.