Уравнение бернулли для элементарной струйки идеальной жидкости

Вспомним уравнение Эйлера для элементарной струйки идеальной жидкости:

Приведем систему уравнений к виду удобному для интегрирования, для чего умножим каждое из уравнений на dx, dy, dz и почленно сложим:

            Первый трехчлен уравнения   является полным дифференциалом гидродинамического давления, отнесенным к единице плотности и равен:   

            Рассмотрим движение жидкости только под действием силы тяжести, тогда внешние массовые силы, заданные в виде проекций ускорений на соответствующие координатные оси, будут X=0, Y=0, Z=-g. Тогда второй трехчлен будет равным – gdz.

Первую часть уравнения   преобразуем зная, что перемещения соответственно равны:    dx = Uxdt, dy = Uydt, dz = Uzdt.

Тогда: 

где U – местная скорость в сечении струйки.

            Подставляя в уравнение   полученные значения, запишем:

  или                  

Если разделить уравнение   на g, получим уравнение, отнесенное к единице веса:

Поле интегрирования получим:

           

Выражение   было получено в 1738 г. академиком Российской Академии наук Д. Бернулли и названо уравнением Бернулли для элементарной струйки идеальной жидкости.

Уравнение Бернулли для элементарной струйки и потока реальной жидкости

Уравнение Бернулли выражает закон сохранения энергии, связывающий удельную по весу энергию жидкости в двух сечениях потока. Для элементарной струйки:

Для потока реальной жидкости

Здесь: z₁, z₂ - расстояния от произвольно выбранной горизонтальной плоскости до центров тяжести рассматриваемых сечений 1,2, p₁,p₂ - давления в центрах сечений, U₁,U₂- местные скорости жидкости в сечениях 1 и 2, V₁,V₂- средние скорости жидкости в сечениях 1 и 2, ρ- плотность жидкости, g-ускорение силы тяжести,  h_1-2 -энергия единицы веса жидкости, потраченная на преодоление сил трения между сечениями 1 и 2.  α - коэффициент Кориолиса (его значение зависит от степени неравномерности распределения скоростей в живом сечении потока, меняясь в пределах от 1 до 2).

Уравнение неразрывности для несжимаемой жидкости.

Равенство нулю этого выражения называют уравнением неразрывности для несжимаемой жидкости в дифференциальной форме и записывается следующим образом:

К такому же выводу можно прийти, основываясь на следующих рассуждениях: если считать жидкость несжимаемой, то условием неразрывности (сплошности) потока можно считать равенство втекающих и вытекающих объёмов, т.е. изменение объёма должно равняться 0. В выражении для dW величины обязательно имеют положительные (не нулевые) значения. Тогда для того, чтобы , нужно выполнение следующего условия: которое и есть уже упомянутое выше уравнение неразрывности для несжимаемой жидкости в дифференциальной форме.

Уравнение неразрывности для сжимаемой жидкости.

Если в уравнение неразрывности добавить слагаемое, учитывающее изменение плотности жидкости во времени 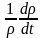, получим формулу, выражающую изменение единичной массы жидкости протекающей за время dt через объём dx, dy, dz. Приравняв это уравнение к нулю:

получим уравнение неразрывности для сжимаемой жидкости в дифференциальной форме.

Его физический смысл заключается в том, что изменение плотности во времени обратно изменению объёма жидкости во времени. Объём же меняется из-за изменения скоростей во времени, т.е. вследствие изменения формы потока.

Последнее выражение есть первое уравнение (условие) в системе дифференциальных уравнений, описывающих движение потока жидкости.