Лекция 4 Линейная модель множественной регрессии.

Вопросы:

1. Линейная модель множественной регрессии в скалярной и векторной формах. МНК оценки коэффициентов множественной регрессии.

2. Ковариационная матрица оценок коэффициентов регрессии. Оценка дисперсии ошибок.

3. Теорема Гаусса-Маркова.

4. Коэффициент детерминации, скорректированный коэффициент

детерминации.

5. Частная корреляция.

6. Проверка статистических гипотез, доверительные интервалы.

1. Линейная модель множественной регрессии в скалярной и векторной формах. Мнк оценки коэффициентов множественной регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1. они должны быть количественно измеримы (качественные показатели могут быть проранжированы);

2. факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной зависимости.

Включаемые факторы должны объяснять вариацию зависимой переменной. Если строится модель с р факторами, то для неё можно определить R² – коэффициент детерминации, который фиксирует долю объясненной вариации признака. Влияние других, не учтенных в модели, факторов оценивается (1–R²) с соответствующей остаточной дисперсией. При дополнительном включении в регрессию (р + 1)-го фактора коэффициент R² должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, то включаемый фактор является лишним. Насыщение модели лишними факторами приводит к статистической незначимости параметров регрессии.

Как и в парной зависимости возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции (степенная легко линеаризуется).

Рассмотрим линейную модель множественной регрессии:

.

По выборке объёма n оценивается уравнение регрессии

,

где неизвестные коэффициенты оцениваются МНК, при котором минимизируется сумма квадратов остатков, позволяя получить систему нормальных уравнений:

Решение системы может быть получено, например, по формулам Крамера:

, при этом

.

Оценим коэффициенты регрессии МНК в матричной форме. Обозначим

, , , ,

Значения признака Матрица объясняющих Вектор Вектор Вектор

переменных, столбцами регрессора j случайных коэффициентов

которой являются X_j ошибок регрессии

Модель множественной регрессии примет вид

,

где Х – детерминированная матрица, Y и - случайные матрицы. Пусть , где - вектор модельных значений. Сумма квадратов остатков минимизируется:

.

Необходимые условия получают дифференцированием по вектору .

.

Аналогично парной регрессии, можно показать, что вектор остатков е всем независимым переменным и S = (1…1)^T, а вектор - есть ортогональная проекция вектора Y на гиперплоскость, образованную S и Х. Кроме того,

, .

Если перейти к стандартизованному масштабу:

, , … , ,

уравнение регрессии примет вид:

,

где коэффициенты могут быть определены из системы уравнений

,

здесь и - парные коэффициенты корреляции.

Вернуться от стандартизованного масштаба к обычному можно с помощью соотношений:

, .

И, наконец, параметры уравнения множественной регрессии можно определить с помощью ППП:

• ППП Excel:

а) Сервис/Анализ данных/Описательная статистика

б) Сервис/Анализ данных/Корреляция

в) Сервис/Анализ данных/Регрессия

• ППП Statgraphic:

а) Describe/Numeric Data/Multiple Variable Analysis/ в доп. меню поставить флажки на Summary Statistics, Correlations, Partial Correlations

б) Relate/Multiple Regression.

Пример. Известны следующие данные (условные) о сменной добыче угля на одного рабочего Y (т), мощности пласта Х₁ (м) и уровне механизации работ Х₂ (%), характеризующие процесс добычи угля на 7 шахтах. Предполагая, что между Y, X₁, X₂ существует линейная корреляционная зависимость, найти её аналитическое выражение.

№	Х1	Х2	Y
1	8	5	5
2	11	8	10
3	12	8	10
4	9	5	7
5	8	7	5
6	8	8	6
7	9	6	6

Решение.

Проверим однородность выборки.

Vy=	30,86067%
Vx1=	17,26919%
Vx2=	20,55514%

Так как все значения меньше 35 %, то выборка однородна, и её можно использовать для анализа.

Вариант решения 1.

Расчет с помощью матричных операций.

Использование матричной формы записи формул и проведения расчетов имеет несколько преимуществ и недостатков.

Преимущества заключаются в том, что запись формул приобретает очень компактный вид: вид формул, представленных в матричном виде, не зависит от количества факторов, включенных в модель, и является очень удобным при расчетах характеристик многофакторных моделей.

Недостатком использования в расчетах матричных формул является необходимость хорошего знания матричной алгебры.

Приведем перечень используемых матричных операций.

Транспонирование – Вставка функции, Категория: Ссылки и массивы, Функции: ТРАНСП.

Вычисление обратной матрицы - Вставка функции, Категория: Математические, Функции: МОБР.

Умножение матриц – Вставка функции, Категория: Математические, Функции: МУМНОЖ.

Выполнение матричных функций имеют следующие особенности:

- для результирующей матрицы нужно выделить необходимое количество ячеек;

- для распространения действий на массив:

• Выделить 1-ю ячейку с расчетами и все ячейки, на которые будет распространено действие функции;

• Нажать и отпустить клавишу «F2»;

• Последовательно нажать, не отпуская, клавиши «Ctrl», «Shift», «Enter», отпустить все три клавиши, и на экране появится содержимое всей матрицы.

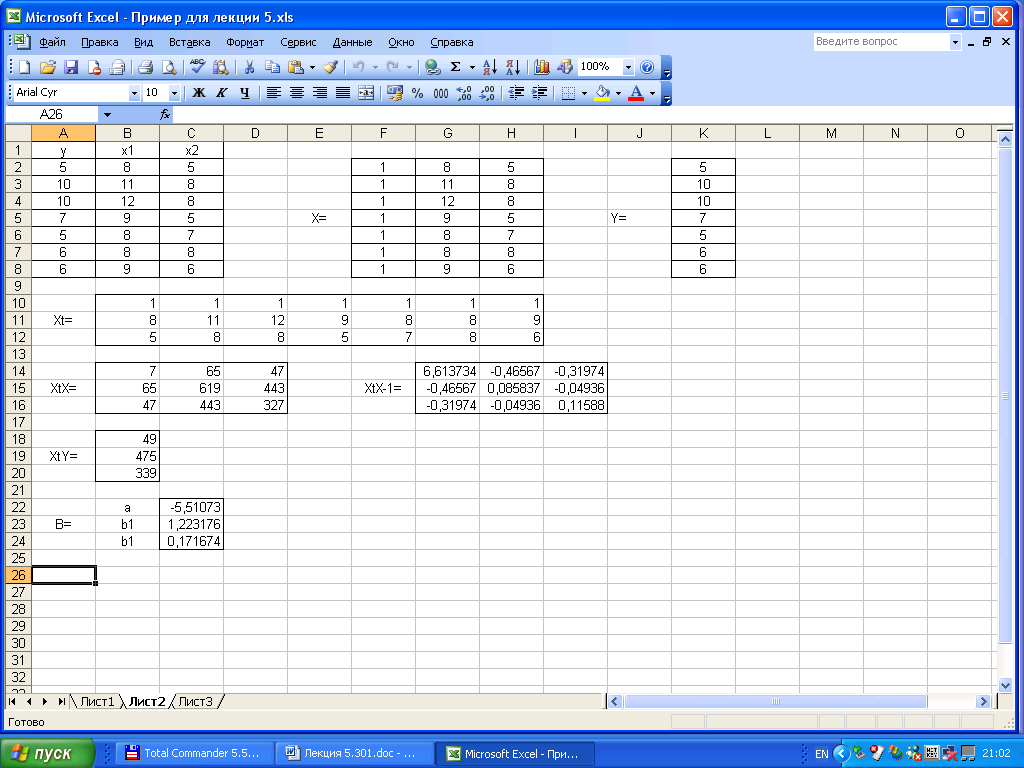
Вариант решения 2.

1) Составим ,

, ,

и

.

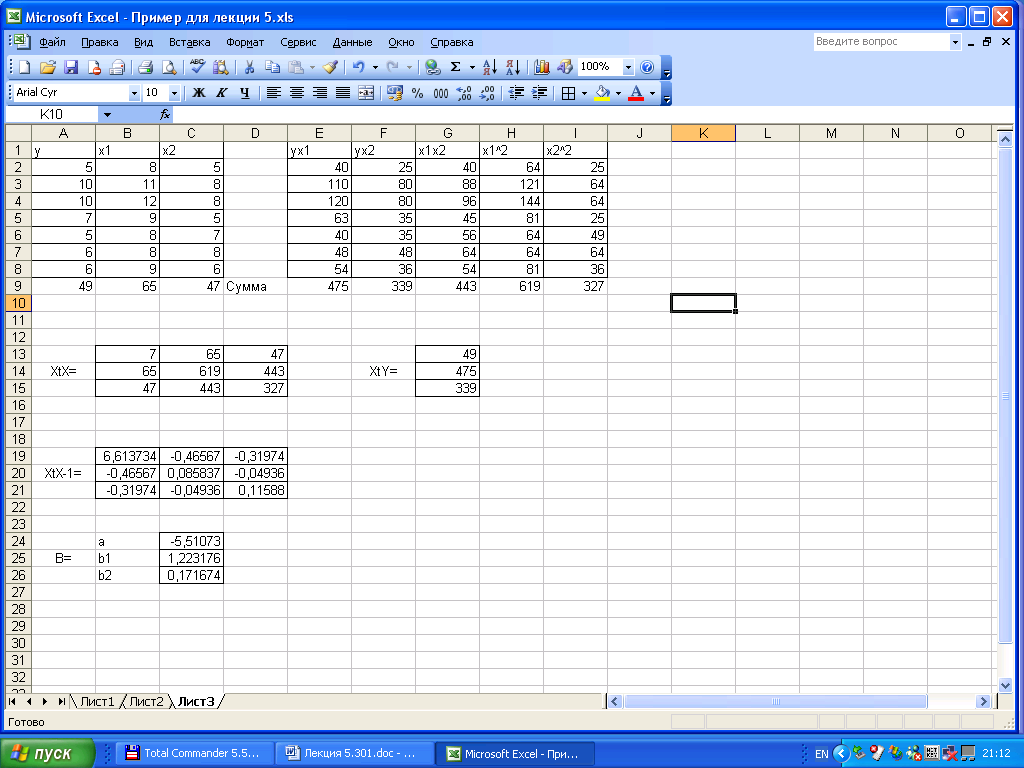
Таким образом, уравнение множественной регрессии примет вид:

.

Вариант решения 3.

Вариант решения 4.

Получим уравнение регрессии в стандартизованном масштабе.

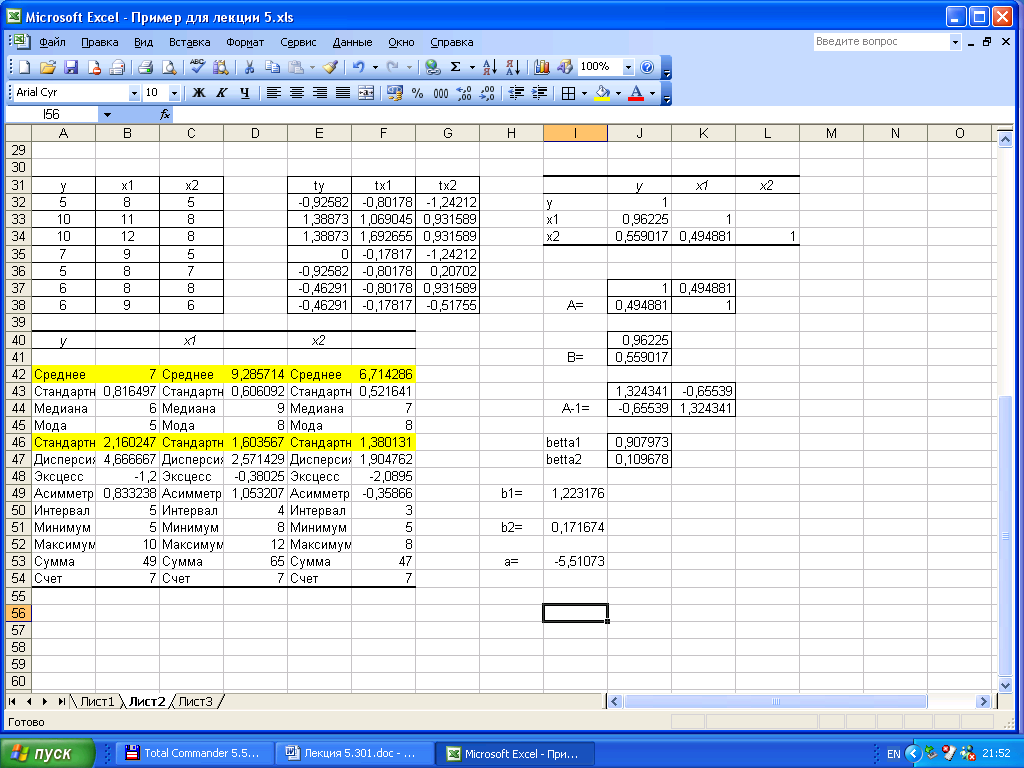
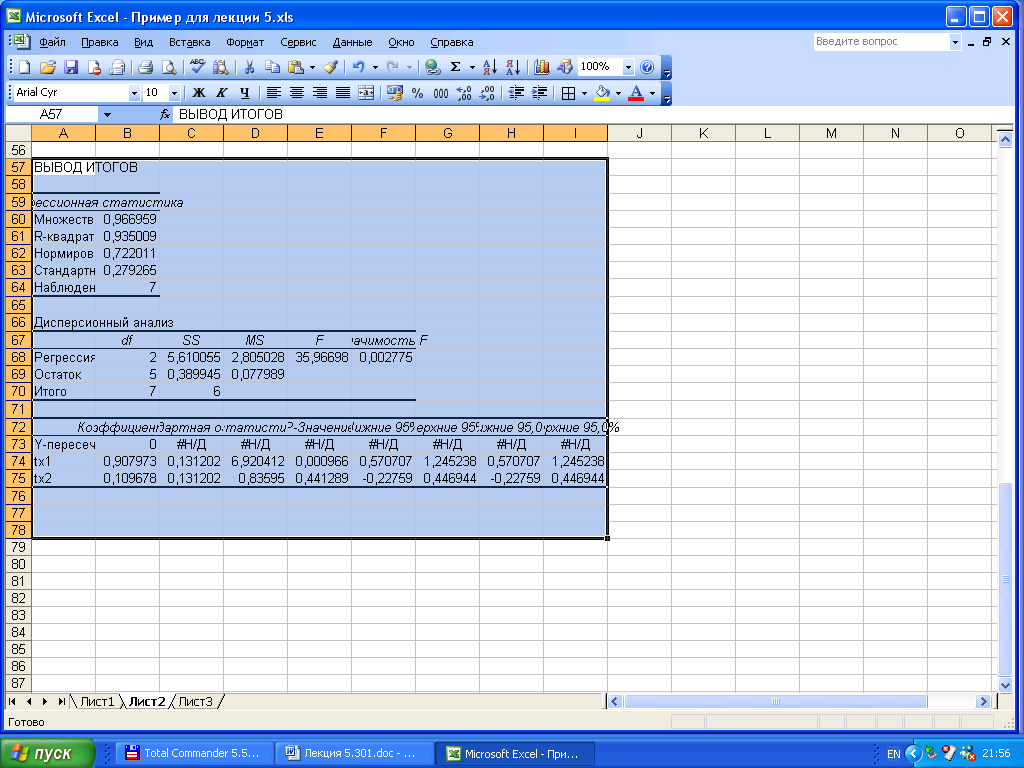
На практике часто бывает необходимо сравнение влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии и средние показатели эластичности Э_j:

, .

Стандартизованный коэффициент регрессии показывает, на сколько величин S_y изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на S_xj, а средний показатель эластичности Э_j – на сколько % (от средней) изменится в среднем Y при увеличении только Х_j на1 %.

Пример.

Для данных предыдущего примера имеем:

1)

2) ;

.