1.3.1. Перенос массы Конвективный механизм. Поток массы в лабораторной системе отсчета за счет конвективного механизма для любой точки системы может быть связан с конвективной скоростью:

, кг/м²с . (1.11)

В случае многокомпонентной среды можно рассмотреть поток массы каждого компонента:

, (1.12)

где i - номер компонента, _i - плотность компонента i.

Зачастую удобнее использовать поток вещества, а не массы:

, кмоль/м²с , (1.13)

где - мольная масса компонента i, кг/кмоль; - мольная концентрация, кмоль/м³. Отметим, что конвективная скорость и потоки рассматривались в лабораторной системе отсчета, т.е. относительно системы отсчета, связанной с аппаратом. В условиях гидромеханического равновесия конвективная скорость относительно аппарата является не просто постоянной, а нулевой величиной.

Молекулярный механизм. Собственно молекулярный механизм переноса массы можно наблюдать в термодинамически равновесной системе при наличии лишь градиентов концентрации меченых частиц сорта i (i'- изотопы молекул сорта i):

. (1.14)

Знак «минус» свидетельствует о противоположной направленности векторов потока вещества и градиента концентрации. Градиент концентрации направлен в сторону максимального увеличения концентрации, а поток вещества - в сторону ее уменьшения, выравнивания неоднородности. Эйнштейном было показано, что коэффициенты пропорциональности в этом соотношении характеризуют средний квадрат смещения молекул за единицу времени вследствие хаотического теплового движения:

. (1.15)

Эти величины называют эйнштейновскими коэффициентами диффузии. Они экспериментально определяются с помощью методов меченых атомов или ядерного магнитного резонанса, а также на основе численного эксперимента методом молекулярной динамики (моделирование движения совокупности частиц на компьютере). зависят от динамических характеристик молекул (масса, потенциал взаимодействия), а также от давления и температуры системы (см. приложение П.3.2). Поскольку характеризуют подвижность молекул, они существенно зависят от фазового состояния системы. В газах имеют порядок 10^-6 м²/с, в жидкостях - 10^-9 м²/с, в твердых телах - 10^-12 м²/с, они увеличиваются с ростом температуры и уменьшения давления.

В соответствии с подходом независимой диффузии предполагается, что в неравновесных условиях собственно диффузионные потоки можно описать эйнштейновскими коэффициен-тами. Тогда для изотермической системы в отсутствие турбулентности поток компонента i складывается из диффузионного и конвективного:

, (1.16)

где n - число компонентов в системе. Следует иметь в виду, что в неравновесных условиях конвективная скорость может появляться и за счет самой диффузии. Поясним на примере. Рассмотрим аппарат, в одной части которого находится компонент 1, а в другой - компонент 2, отделенные друг от друга перегородкой. Давление и температура в обеих частях аппарата одинаковы. Если убрать перегородку, то за счет молекулярной диффузии возникнут противоположно направленные потоки компонентов. Однако величины потоков будут различны вследствие отличия динамических характеристик молекул компонентов и, следовательно, эйнштейновских коэффициентов диффузии . Допустим , тогда учитывая, что из соотношения Гиббса-Дюгема , диффузионный поток первого компонента будет больше второго. Молекулярный механизм вызовет суммарный перенос вещества из первой части аппарата во вторую, что приведет к возникновению в закрытом аппарате градиента плотности числа частиц и соответственно давления . А это вызовет противоположно направленный конвективный поток, выравнивающий градиент давления (рис. 1.2).

Рис. 1.2. Диффузийные потоки и конвективная ско­рость, вызванная диффузией в закрытом аппарате

Таким образом, в неравновесных условиях наблюдать и изучать в чистом виде молекулярный перенос массы затруднительно, так как это требует искусственного поддержания постоянства давления в системе. Сложность представляет экспериментальное определение величин и конвективной скорости . Даже измерив в лабораторной системе отсчета потоки всех компонентов и поля концентраций c_i, нельзя разрешить систему n уравнений (1.16), поскольку она содержит n+1 неизвестную величину (D_i, ). Поэтому обычно диффузионные потоки определяют в системе отсчета, скорость движения которой относительно лабораторной устанавливается достаточно просто. Как правило, используют среднемассовую или среднеобъемную системы отсчета. Система отсчета задается условием равенства нулю суммарного потока соответствующего признака (обозначим его z_i) в данной системе отсчета:

. (1.17)

В среднемассовой системе отсчета z_i=m_i (мольная масса компонента), а в среднеобъемной z_i=V_i (парциальный мольный объем компонента V_i, м³/кмоль):

.

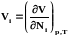Тогда мольный поток компонента i в лабораторной системе отсчета можно представить в виде

, (1.18)

, (1.19)

где - скорость движения соответствующей системы отсчета относительно лабораторной, которая может быть найдена, если измерены экспериментально величины потоков . В соответствии с подходом независимой диффузии потоки в системе отсчета z имеют вид

, (1.20)

где - конвективная скорость в системе отсчета z.

Используя дополнительное уравнение (1.17), можно выразить через , , , и представить потоки в виде

. (1.21)

На практике удобнее использовать коэффициенты диффузии, связывающие потоки не с градиентами химических потенциалов, а с градиентами концентрации. Выражая химические потенциалы через мольные концентрации и используя соотношение

,

позволяющее сократить на единицу число независимых переменных, можно записать

. (1.22)

Таким образом, макроскопический поток каждого компонента в системе отсчета z зависит от градиентов концентраций всех компонентов, а коэффициенты пропорциональности носят название матрицы коэффициентов многокомпонентной диффузии и определяются как свойствами компонентов среды, так и выбором системы отсчета. Экспериментальное нахождение коэффициентов диффузии осуществляется, как правило, в замкнутом приборе. В этих условиях суммарный поток объема равен нулю, т.е. лабораторная система отсчета совпадает со среднеобъемной. Поэтому экспериментальные данные по коэффициентам диффузии обычно приводятся для среднеобъемной системы отсчета. В частном случае двухкомпонентной системы матрица вырождается в единственный коэффициент бинарной (взаимной) диффузии :

. (1.23)

Это соотношение называется первым законом Фика. Используя подход независимой диффузии, можно выразить коэффициенты взаимной диффузии через эйнштейновские коэффициенты:

. (1.24)

Можно сделать это и для многокомпонентных смесей, связав элементы матрицы с _{(см. приложение П.3.1)}. Следует помнить о зависимости коэффициентов диффузии (кроме эйнштейновских) от выбора системы отсчета. Так, например, в среднемассовой системе отсчета коэффициенты бинарной диффузии не обладают свойством симметрии и могут быть выражены через :

(1.25)

При межфазном переносе вещества потоки зачастую записывают относительно границы раздела фаз. При этом, как правило, один или несколько компонентов через границу раздела фаз не переносятся (инертные компоненты). Для бинарной смеси, первый компонент которой переходит границу раздела фаз, а второй нет, потоки в одной фазе запишутся в системе отсчета с нулевым потоком второго компонента:

, (1.26)

. (1.27)

Выразив из (1.27) и подставив в (1.26), можно получить соотношения для коэффициентов бинарной диффузии в системе отсчета, соответствующей нулевому потоку второго компонента,

; . (1.28)

При , что наглядно демонстрирует бесконечно большой диапазон изменения коэффициентов бинарной диффузии в зависимости от выбора системы отсчета. Влияет выбор системы отсчета и на элементы , они могут принимать как положительные, так и отрицательные значения. Только эйнштейновские коэффициенты диффузии (1.15) не зависят от выбора системы отсчета, всегда положительны и имеют ясный физический смысл.

Связь макро- и микроуровней описания явлений осуществляется статистической механикой, позволяющей с использованием неравно-весных функций распределения молекул по скоростям f_i^н получить выражения для макроскопических потоков и коэффициентов переноса:

. (1.29)

Турбулентный механизм. Турбулентный перенос массы можно рассматривать по аналогии с молекулярным как следствие хаотического перемещения вихрей. Вводится коэффициент турбулентной диффузии , зависящий как от свойств среды, так и от неоднородности скорости и удаленности от межфазной поверхности. При турбулентном движении суммарный поток вещества относительно лабораторной системы отсчета может быть записан как

(1.30)

или

, (1.31)

. (1.32)

Для системы отсчета, в которой поток компонента n равен нулю,

, (1.33)

, (1.34)

где - символ Кронекера.

Для двухкомпонентной смеси можно ввести коэффициенты турбулентной диффузии в соответствующей системе отсчета:

. (1.35)

Для среднеобъемной системы отсчета , а для среднемассовой . Поскольку объемы среды, участвующие в турбулентных пульсациях, значительно превышают молекулярные размеры, интенсивность турбулентного переноса массы может быть существенно выше молекулярного. Отношение коэффициентов турбулентной и молекулярной диффузии в пристенной области достигает .