3.5.2. Математическое моделирование структуры потоков

Наиболее корректной математической моделью структуры потоков в аппарате является исчерпывающее описание. Решение системы уравнений неразрывности и движения совместно с условиями однозначности позволило бы найти поле скорости в аппарате. Однако получить такое решение для большинства случаев невозможно. Поэтому на практике идут по пути упрощения модели, используя для характеристики структуры потока функцию распределения времени пребывания элементов потока в аппарате. Рассмотрим последовательно этапы математического моделирования структуры потока (см. 3.1) на примере однофазного течения в горизонтальном полом цилиндрическом проточном аппарате.

На рис. 3.2 показаны экспериментально найденные профили скорости W_х в некоторых сечениях. Поскольку движение считается осесимметричным, в верхней половине аппарата распределение скорости будет иметь аналогичный вид. Как видим, поле скорости даже такого простого аппарата имеет существенную неоднородность.

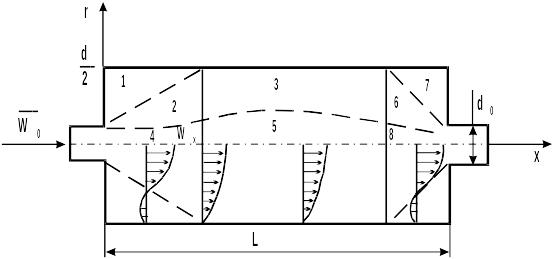
Рис. 3.2. Поле скорости W_x и характерные зоны в горизонтальном цилиндрическом проточном аппарате: 1, 7 - застойные зоны; 2, 6 - зоны смешения; 3 - пограничный слой; 4, 5, 8 - ядро потока

Можно выделить две наиболее упрощенные идеализированные модели, характеризующие предельные ситуации: идеальное вытеснение и идеальное смешение, а также более реалистичные модели промежуточного типа, к которым относятся ячеечная и диффузионная модели.

Модель идеального вытеснения. Согласно модели идеального вытеснения (МИВ), все элементы потока движутся по параллельным траекториям с одинаковыми скоростями (рис. 3.3). Время пребывания в аппарате для всех элементов такого потока одинаково.

Рис. 3.3. Поле скорости W_x для модели идеального вытеснения

Приведенное выше словесное описание МИВ является вербальной моделью. Для получения соответствующей математической модели введем понятие концентрации меченых элементов потока в аппарате. Зная изменение этой величины во времени, можно определить функцию распределения времени пребывания элементов потока в аппарате. В общем случае для нахождения такого поля концентраций необходимо было бы воспользоваться исчерпывающим описанием. Однако сделанные допущения позволяют его значительно упростить. Во-первых, допущение о равенстве и постоянстве скоростей всех элементов потока позволяет сократить размерность задачи до одномерной, совместив ось X с направлением вектора скорости; во-вторых, отпадает необходимость решения уравнений неразрывности и движения для определения скорости, так как она может считаться заданной; в-третьих, отсутствие перемешивания элементов потока позволяет считать равными нулю коэффициенты диффузии ( , ) в уравнении (2.27). Тогда

(3.11)

или для одномерного случая

, (3.12)

где c=c(x,t) - концентрация меченых элементов потока в сечении аппарата с координатой x в момент времени t. Для нахождения решения необходимо дополнить уравнение (3.12) начальными и граничными условиями.

Нашим целям описания времени пребывания элементов потока в аппарате наилучшим образом соответствуют условия, смысл которых заключается в том, что элементы потока помечены только в нулевой момент времени и только на входе в аппарат. Поскольку число меченых элементов N_М конечно, а толщина слоя на границе аппарата, в котором они распределены, стремится к нулю, их концентрация в сечении x=0 в момент времени t=0 стремится к бесконечности.

- начальное условие; - граничное условие;

, (3.13)

где c₀ - средняя концентрация меченых элементов потока в аппарате в начальный момент времени; N_М - количество помеченных элементов; V_а - объем аппарата; , - дельта-функция Дирака (см. приложение П.1.4). Совместное решение (3.12) и (3.13) позволяет получить c(x,t) - изменение концентрации меченых элементов потока по координате X и по времени t.

Для достижения нашей цели достаточно знать решение в сечении x=L, т.е. на выходе из аппарата. Оно имеет вид

, . (3.14)

Концентрация меченых элементов потока, выходящих из аппарата в момент времени t, пропорциональна количеству элементов, пребывающих в аппарате это время. Используя определение функции распределения (3.6), можно выразить ее следующим образом:

, (3.15)

или

. (3.16)

Вид этой функции изображен на рис. 3.4. Полученные результаты имеют достаточно простой физический смысл. Поскольку все элементы потока движутся с одинаковой скоростью, они будут иметь одинаковое время пребывания в аппарате, совпадающее со средним (3.14). И если мы пометим элементы потока в узком слое на входе в аппарат, то выйдут они из аппарата все вместе через промежуток времени t =  , что обеспечит бесконечно большое значение f( )= , тогда как для любого t f(t)=0.

Рис. 3.4. Вид функций распределения для различных моделей при определенных значениях параметров: m - числа ячеек (ячеечная модель) и Ре_L - критерия Пекле для продольного перемешивания (диффузионная модель)

Разумеется, на практике такая ситуация никогда не реализуется, так как для этого необходимо движение потока без трения на границах. Наиболее близка к МИВ структура турбулентного потока, движущегося по трубе при L/d>>1.

Модель идеального смешения. Другой крайне идеализированной, но противоположной по смыслу моделью является модель идеального смешения (МИС). Предполагается, что любая порция входящего в аппарат потока мгновенно равномерно перемешивается во всем объеме. Координаты и скорость отдельного элемента потока в каждый момент времени, а также время его пребывания в аппарате имеют чисто случайное значение. Концентрация меченых элементов потока одинакова во всех точках аппарата.

Для получения математической модели МИС нет необходимости использовать исчерпывающее описание, представляющее собой локальную форму законов сохранения. Поскольку концентрация меченых элементов потока предполагается одинаковой во всех точках аппарата проще воспользоваться интегральной формой закона сохранения массы (т.е. для всего аппарата) или, точнее, его аналогом - законом сохранения количества меченых элементов потока.

По аналогии с (2.2) можно записать

, (3.17)

где G_Nвх, G_Nвых - количество меченых элементов потока, входящих в аппарат и выходящих из него за единицу времени. Как и при рассмотрении МИВ, пометим элементы потока лишь в начальный момент времени. При любых t>0 входа меченых элементов в аппарат не будет (G_Nвх=0,t>0). G_Nвых можно определить через объемный расход выходящего потока и концентрацию в нем меченых элементов (она будет соответствовать их концентрации в самом аппарате). Так как концентрация c(x,t) одинакова во всех точках аппарата, ее можно считать функцией одного аргумента c(x,t)=c(L,t)=c(t), обозначив для краткости c:

. (3.18)

Из уравнения (3.17)

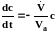(3.19)

или с учетом (3.9)

. (3.20)

Интегрируя уравнение (3.20) с начальными условиями c(0) = c₀, получим

; . (3.21)

Воспользовавшись соотношением (3.15) можно определить функцию распределения (см.рис.3.4):

, (3.22)

. (3.23)

Наиболее близка к МИС структура маловязкого потока, движущегося с небольшой расходной скоростью через аппарат с интенсивно работающей мешалкой.

Ячеечная модель. Более реалистичной моделью является ячеечная модель (МЯ), в соответствии с которой предполагается последовательное прохождение потоком ряда ячеек идеального смешения. Параметром модели служит число таких ячеек m. Учитывая, что объем каждой ячейки равен отношению объема всего аппарата к числу ячеек, а концентрация меченых элементов потока на входе в ячейку соответствует их концентрации на выходе из предыдущей, можно получить для i-й ячейки по аналогии с (3.20) из (3.17)

. (3.24)

Решение системы m дифференциальных уравнений (3.24) дает выражение для концентрации меченых элементов в последней ячейке, т.е. на выходе из аппарата c_m(t), а затем и для функции распределения по (3.15):

. (3.25)

Нетрудно убедиться, что при m=1 МЯ переходит в МИС, а при m= - в МИВ (рис. 3.4). Наиболее приемлемое описание МЯ дает для каскада аппаратов с мешалками и других аппаратов ступенчатого типа.

Диффузионная модель. Другой моделью промежуточного типа является диффузионная модель (МД). Считается, что отклонение в движении элементов потока от идеального вытеснения осуществляется за счет их случайных блужданий, которые могут быть описаны по аналогии с молекулярным или турбулентным механизмом переноса. Это позволяет воспользоваться уравнением нестационарной конвективной диффузии для определения концентрации меченых элементов потока c(x,t), полагая конвективную скорость равной для всех элементов, а перемешивание вне зависимости от причин его вызывающих учитывать с помощью коэффициента обратного (продольного) перемешивания D_L. Тогда из (2.27) получим

. (3.26)

Функция распределения для аппарата конечной длины получена в виде суммы бесконечного ряда. Для полубесконечного аппарата (L  ) найдено решение, которое может быть использовано в качестве приближенного при больших L/d (Pe_L > 10)

, (3.27)

где Pe_L=W_xL/D_L - критерий Пекле для продольного перемешивания (параметр модели). При Pe_L=0 МД переходит в МИС, а при Pe_L= - в МИВ (рис. 3.4).

Необходимо помнить, что D_L учитывает суммарное отклонение от идеального вытеснения за счет всех механизмов переноса (конвективного, турбулентного, молекулярного) и не может отождествляться с коэффициентом турбулентной или молекулярной диффузии. Обычно МД применяют для аппаратов, характеристики потоков в которых изменяются по длине непрерывно.

Нами рассмотрены наиболее простые модели структуры потоков в аппаратах. Существуют и более сложные, например, двухпарамет­рическая диффузионная модель учитывает перемешивание не только в продольном, но и в радиальном направлении коэффициентом D_r (двумерная постановка задачи c(x,r,t)). В сложных случаях применяют комбинированные модели, описывая различные характерные зоны аппарата разными математическими моделями. Однако предоставляя возможность более точно воспроизвести структуру потока в реальном аппарате, сложные модели обладают и недостатком - трудностью определения большого числа параметров. Таким образом, мы подходим ко второму этапу математического моделирования.

Идентификация модели. Под идентификацией модели понимается определение неизвестных параметров. Таковыми, например, являются критерий Пекле для продольного перемешивания Ре_L в диффузионной модели, и число ячеек m в ячеечной модели. Как правило, для их определения используют экспериментальные данные, полученные методом меченых объемов. Для этого в основной поток на входе в аппарат вводится индикатор (трассер), элементарные объемы которого должны двигаться аналогично элементам основного потока, но иметь отличия в окраске, электропроводности, оптической плотности и т.д., позволяющие измерить их концентрацию в основном потоке. В качестве индикаторов используют красители, растворы солей, радиоактивные изотопы. Фиксируя изменение во времени концентрации индикатора на выходе из аппарата, получают кривую отклика C(t).

Обычно применяют импульсный ввод индикатора, т.е. единовременное заполнение небольшим объемом индикатора всего поперечного сечения на входе в аппарат, что соответствует начальным и граничным условиям (3.13). В этом случае кривая отклика С(t) = с(L,t) связана соотношением (3.15) с функцией распределения времени пребывания элементов потока в аппарате f(t). Затем, определив среднее время пребывания по (3.8), переходят к безразмерной функции распределения f*() (3.10) и, сопоставляя ее с известными зависимостями для различных моделей структуры потоков (рис. 3.4), выбирают наиболее приемлемую модель.

Теперь можно перейти непосредственно к нахождению параметров модели, которое, как правило, осуществляется с помощью метода моментов. В случае однопараметрической модели обычно используется

второй центральный момент или дисперсия _^ Дисперсией случайной величины называется средний квадрат ее отклонения от среднего значения.

Имея в виду, что интегрирование случайной величины с функцией распределения представляет процедуру осреднения, получим

. (3.28)

Подставив в (3.28) теоретические решения f*() для различных моделей, можно найти связь дисперсии с искомыми параметрами:

(МЯ) , (3.29)

(МД) . (3.30)

Итак, для определения параметров необходимо знать экспериментальное значение дисперсии. На практике, исходя из вида кривой отклика, выбирают временной интервал t для фиксации численных значений концентрации индикатора на выходе из аппарата, обеспечивающий достаточно точное воспроизведение непрерывной кривой отклика С(t) дискретными значениями С_i=C(t_i). Интегрирование приближенно заменяется суммированием, например, тогда вместо (3.15) и (3.28) будем иметь

, (3.31)

, (3.32)

где n - число дискретных точек на кривой отклика; . Подставляя экспериментальное значение дисперсии в уравнения типа (3.29), (3.30), находят из них параметры модели.

Для дальнейшего использования модели требуется, как правило, знание зависимости параметров модели от конструктивных особенностей, масштабов аппарата и режимных условий проведения процесса. Для рассматриваемого примера проточного аппарата это d₀, L, d, , физические свойства среды. Таким образом, идентификация модели является весьма трудоемкой задачей, требующей значительных материальных затрат и продолжительных экспериментальных исследований.

Проверка адекватности модели. Учитывая, что любая модель дает лишь приблизительное описание реального объекта, необходимо проверить, насколько хорошо она воспроизводит экспериментальные результаты. Для этого можно сопоставить рассчитанную с использованием найденных параметров функцию распределения f*^p() с экспериментальной f*^Э(). Если точность удовлетворительна, то считают модель адекватной оригиналу, если нет, то выбирают другую, возможно более сложную модель.

Использование модели для описания и оптимизации объекта-оригинала. Как уже отмечалось, гидродинамическая структура потоков в аппарате существенно влияет на характер протекания тепло- и массообменных процессов. Применение простейших моделей структуры потоков вместо исчерпывающего описания позволяет значительно упростить расчет соответствующего оборудования. Например, для нахождения осредненного по поперечному сечению нестационарного поля температур Т(х,t) в теплоизолированном проточном аппарате систему уравнений Фурье - Кирхгофа, движения и неразрывности можно заменить одним уравнением с использованием диффузионной модели:

. (3.33)

Расчет различных вариантов позволяет найти оптимальные значения d₀, L, d, _, физических свойств среды, обеспечивающие наилучшее проведение процесса.