Основные принципы управления несущими колебаниями

Совместное использование колебаний несущих и масштабных частот позволяет преодолеть трудности .связанные с разрешением неоднозначности и обеспечением необходимой точности измерений. Вместе с тем возникает необходимость введения в схему дальномера дополнительных средств .позволяющих управлять одним из параметров колебаний. Сам процесс управления колебаниями называется модуляцией, а устройства, осуществляющие этот процесс модуляторами. Колебания, возникающие в результате модуляции называются, модулированными.

При модулировании гармонических колебаний возможное количество видов модуляции ограничивается числом параметров гармонического колебания. Согласно уравнению гармонических колебаний таких параметров три, амплитуда 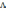, частота (или круговая частота ) и начальная фаза .

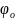В зависимости от того, какой из параметров несущих колебаний подвергается изменениям, различают три вида модуляции: амплитудную, частотную и фазовую. Все эти три вида модуляции находят применение в дальномерной технике.

Рассмотрим один из видов модуляции, а именно амплитудную модуляцию. Известно, что основным уравнением гармонических колебаний является уравнение вида:

Будем гармонически менять амплитуду этих колебаний во времени с круговой частотой 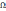, т.е.

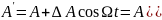
А – амплитуда несущих колебаний при отсутствии модуляции;

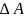– максимальное изменение амплитуды несущих колебаний; 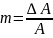– коэффициент, характеризующий относительные изменения амплитуды А и называемый коэффициентом глубины мо­дуляции.

Коэффициент является основным параметром амплитудной мо­дуляции.

Для передачи модулирующих колебаний с наименьшим искажением необходимо, чтобы их частота была значительно ниже частоты несущих колебаний, т.е. 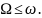Обычно на практике выполняют условие 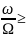100.

Формула амплитудно-модулированных (АМ) колебаний будет иметь вид:

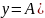(25)

Коэффициент модуляции – m может изменяться в пределах от 0 до1.

Следовательно, такие простейшие AM колебания можно рассматривать как сумму трёх гармонических колебаний с частота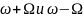ми , при чём первая из них носит назва­ние основной или несущей а две последние – верхней и нижней боковыми частотами.

Наглядное представление об AM колебаниях, состоящих из трёх составляющих компонентов даёт векторная диаграмма. Вектор ОА колебаний несущей частоты имеет длину А, которая характеризует амплитуду колебаний несущей частоты. Он вращается с угловой скоростью . Векторы АБ и АС с амплиту­дами вращаются с угловыми скоростями , что эквивалентно вращению этих векторов относительно вектора ОА с угловой скоростью Ω в противоположные стороны. Сумма всех трёх векторов соответствующая AM колебанию представлена вектором OD. Этот вектор всегда совпадает по направлению с век­тором несущей частоты ОА, что свидетельствует о его вращении с неизменной угловой скоростью . Что касается его длины, то она периодически изменяется по мере вращения векторов АВ и АС относительно вектора ОА. Это означает, что AM колебание имеет постоянную частоту, но изменяющуюся во времени амплитуду.