Тема 6. Оценка эффективности управления портфелем

6.1. Оценка доходности и риска

Наиболее просто определяется доходность портфеля, если некоторая сумма средств инвестируется на определенный период времени. В этом случае доходность портфеля за период определяется по формуле:

, (6.1)

где P – стоимость портфеля в начальный момент времени;

P_n – стоимость портфеля в конечный момент времени.

Рассматриваемый период может быть любым, например, месяц, квартал, год, несколько лет и т. д. Для того, чтобы сравнить доходность одного портфеля с другим, показатели их доходности необходимо привести к единому временному периоду, как правило, году.

Если срок инвестирования меньше одного года, то для определения годовой доходности. как правило, используется формула простых процентов:

, (6.2)

где t – срок инвестирования в днях.

Если срок инвестирования больше года, то для определения годовой доходности портфеля используется формула сложных (эффективных) процентов:

, (6.3)

где n – срок инвестирования в годах.

Случаи, когда портфель формируется за счет инвестирования какой-либо суммы только в начальный момент и на весь период времени, являются скорее исключением, чем правилом. Обычно в ходе управления портфелем средства как изымаются, так и дополнительно вносятся. Если дополнительные средства вносятся или изымаются из портфеля вскоре после начала инвестиционного периода или незадолго до его окончания, то ими можно пренебречь и не учитывать при оценке доходности, так как влияние данных сумм на итоговый результат будет незначительным. Задача усложняется, если приток или изъятие средств происходит в иные моменты времени. Для таких условий теория предлагает два показателя оценки доходности: внутреннюю доходность, и доходность на основе средней геометрической.

Внутренняя доходность определяется исходя из решения следующего уравнения относительно r_p:

, (6.4)

где CF_i – сумма i-го внесения (изъятия) денежных средств инвестором,

t_i- срок, от начального момента до момента i-го внесения (изъятия) денежных средств.

Таким образом, внутренняя доходность представляет собой ставку дисконтирования, приравнивающую потоки платежей, которые осуществлялись в период его управления (внесения и изъятия средств), и стоимость в конце периода к стоимости в начале периода.

Для определения доходности портфеля более точным является метод геометрической средней. Недостаток метода внутренней доходности в том, что во многом на итоговое значение доходности портфеля окажут влияние действия клиентов по изъятию и инвестированию средств. Поэтому доходность портфеля следует рассчитывать по методу средней геометрической:

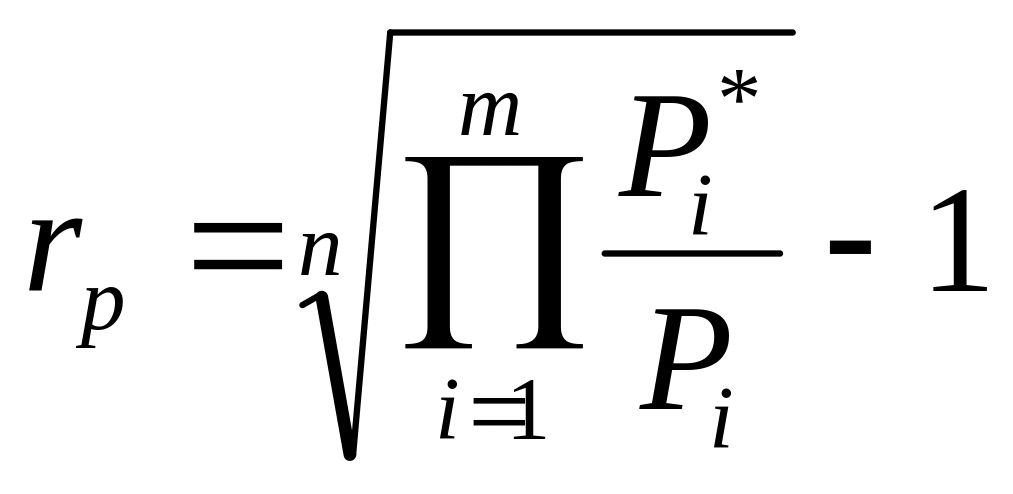, (6.5)

где P_i - стоимость портфеля в начале i-го периода времени,

P_i^* - стоимость портфеля в конце i-го периода времени.

Определить доходность портфеля для случая, когда в процессе управления из него изымались или добавлялись суммы денег, можно с помощью методы оценки стоимости единицы капитала. Суть метода состоит в следующем. В начале периода управления портфелем инвестированная сумма представляется как определенное количество единиц капитала, и рассчитывается стоимость одной единицы капитала. На момент добавления или изъятия средств из портфеля определяется текущая стоимость единицы капитала на основе полученных менеджером результатов. изымаемая или добавляемая сумма денег также представляется в количестве единиц капитала с учетом их текущей стоимости. Рассчитанное количество единиц капитала соответственно отнимается или прибавляется к начальному количеству единиц капитала в портфеле. Аналогичные расчеты осуществляются при каждом изъятии или добавлении средств в портфель.

Изъятия или добавления средств приводят не к изменению стоимости единицы капитала, а только к изменению стоимости портфеля. По результатам управления рассчитывают темп прироста стоимости единицы капитала за весь период. Поскольку стоимость единицы капитала определяется на основе фактических результатов, полученных менеджером, а не вследствие добавления или изъятия денег из портфеля, то прирост стоимости единицы капитала за период управления портфелем эквивалентен показателю доходности портфеля.

Кроме определения доходности портфеля оценка деятельности управляющего предполагает определение фактического риска портфеля за рассматриваемый период. Риск широко диверсифицированного портфеля измеряется величиной бета, слабо диверсифицированного — стандартным отклонением.

Бета показывает зависимость между доходностью актива (портфеля) и доходностью рынка. Доходность рынка — это доходность рыночного портфеля. Поскольку невозможно сформировать портфель, в который бы входили все финансовые активы, то в качестве него принимается какой-либо биржевой индекс с широкой базой. Поэтому доходность рынка — это доходность портфеля, представленного выбранным индексом.

Величина бета (β) представляет собой не что иное как угловой коэффициент наклона линии регрессии доходности актива (портфеля) r_i на доходность индекса r_m:

.

Исходя из этого бета может бы вычислена по формуле:

или , (6.6)

где - ковариация доходности i-го актива (портфеля) с доходностью рыночного портфеля (индекса);

корреляция доходности i-го актива (портфеля) с доходностью рыночного портфеля (индекса);

- дисперсия доходности i-го актива (портфеля);

- дисперсия доходности рыночного портфеля (индекса).

Поскольку величина бета определяется по отношению к рыночному портфелю, то бета самого рыночного портфеля равна единице, так как ковариация доходности рыночного портфеля с самим собой есть его дисперсия, отсюда

.

Бета актива (портфеля) без риска равна нулю, потому что нулю равна ковариация доходности актива (портфеля) без риска с доходностью рыночного портфеля.

Величина β актива (портфеля) говорит о том, насколько его риск больше или меньше риска рыночного портфеля. Активы с бетой больше единицы более рискованны, а с бетой меньше единицы — менее рискованны чем рыночной портфель. Относительно величины бета активы делят на агрессивные и защитные. Бета агрессивных активов больше единицы, а защитных — меньше единицы. Если бета актива равна единице, то его риск равен риску рыночного портфеля.