3.3 Метод Рунге-Кутта
Для повышения точности
вычисления значений функции требуется
проведение дополнительных вычислений
внутри интервала h,
то есть между хi
и хi+1.
Метод Рунге-Кутта даёт
набор формул для расчёта координат
внутренних точек, требуемых для достижения
точности, то есть ошибки на каждом шаге,
порядка h . Расчёты
при использовании этого метода
производятся по формуле
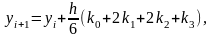 (3.9)
(3.9)
где
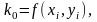 (3.10)
(3.10)
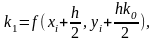 (3.11)
(3.11)
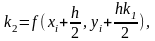 (3.12)
(3.12)
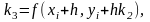 (3.13)
(3.13)
Метод
Эйлера и его модификация по сути дела
являются методами Рунге-Кутта первого
и второго порядка соответственно. По
сравнению с ними метод Рунге-Кутта
обеспечивает более высокую точность,
что позволяет увеличить шаг интегрирования
h. Допустимая
погрешность на
шаге определяет его максимальную
величину.
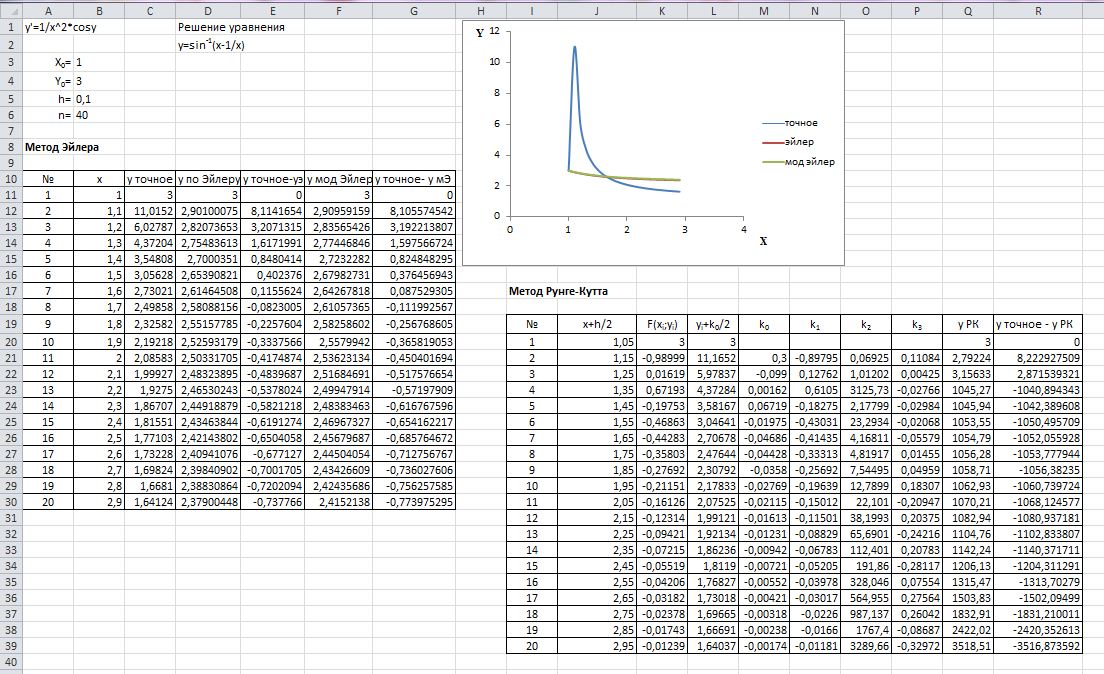
Таблица 3.1 – Вид экрана MS Excel в режиме
отображения значений
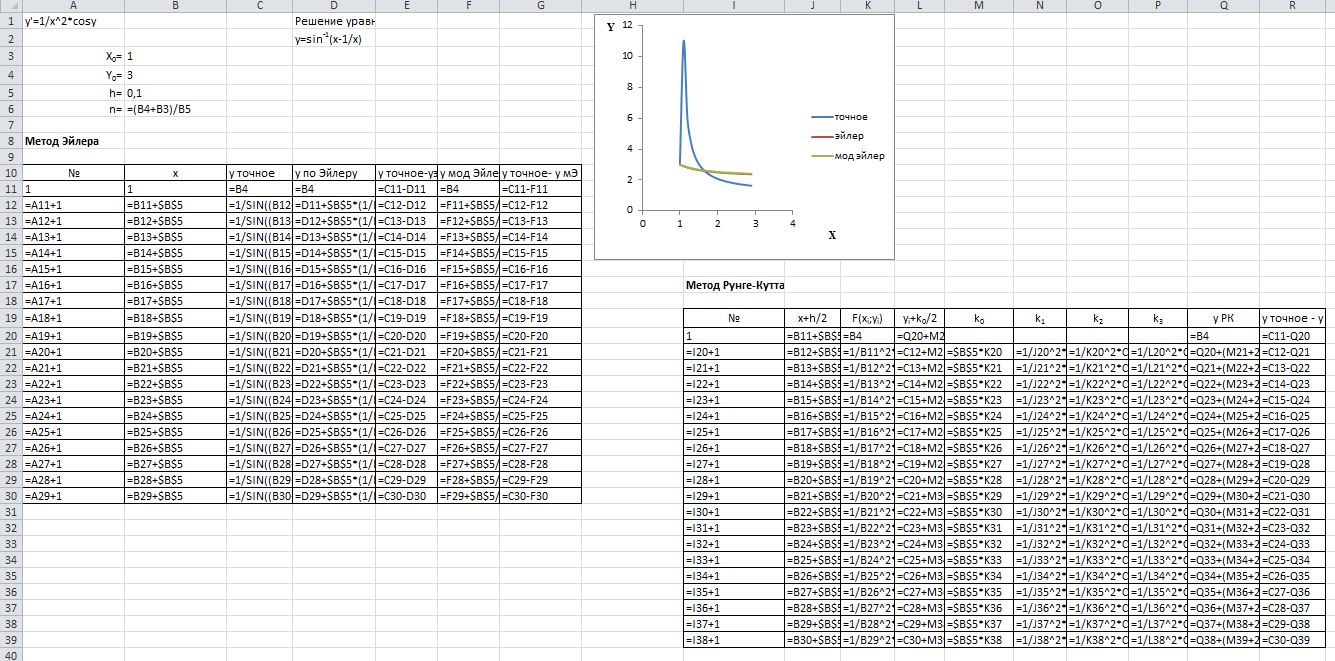
Таблица 3.2 – Вид экрана MS Excel в режиме
отображения формул


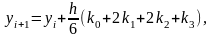 (3.9)
(3.9)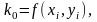 (3.10)
(3.10)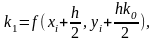 (3.11)
(3.11)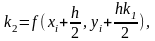 (3.12)
(3.12)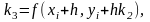 (3.13)
(3.13)
