М ИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Кафедра технологии ЦБП

^{(наименование кафедры)}

Немирова Мария Андреевна

_{(фамилия, имя, отчество студента)}

Институт ТиПХ Курс I Группа 513

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

По дисциплине

Численные методы в химии и химической технологии

На тему

Численные методы решения математических задач химической технологии

(наименование темы)

Отметка о зачёте
						(дата)

Руководитель доцент Я.В. Казаков

_{( должность) (подпись ) ( И.О.Фамилия )}

____________

^(дата)

Архангельск

2012

ЛИСТ ДЛЯ ЗАМЕЧАНИЙ

Оглавление

1 ОТДЕЛЕНИЕ КОРНЕЙ УРАВНЕНИЯ (x-3)cosx-1=0 ГРАФИЧЕСКИ И УТОЧНЕНИЕ ОДНОГО ИЗ НИХ ЧИСЛЕННЫМ МЕТОДОМ С ЗАДАННОЙ ТОЧНОСТЬЮ ɛ 5

1.1 Метод Ньютона (метод касательных) 5

1.2 Метод половинного деления 6

1.3 Метод хорд (метод ложного положения) 8

2 ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ЧИСЛЕННЫМИ МЕТОДАМИ 10

2.1 Метод левых прямоугольников 10

2.2 Метод трапеций 10

2.3 Метод Симпсона (метод парабол) 11

3 СРАВНИТЕЛЬНАЯ ОЦЕНКА РЕЗУЛЬТАТОВ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ y’= 13

3.1 Метод Эйлера 13

3.2 Модифицированный метод Эйлера 14

3.3 Метод Рунге-Кутта 14

1 ОТДЕЛЕНИЕ КОРНЕЙ УРАВНЕНИЯ (x-3)cosx-1=0 ГРАФИЧЕСКИ И УТОЧНЕНИЕ ОДНОГО ИЗ НИХ ЧИСЛЕННЫМ МЕТОДОМ С ЗАДАННОЙ ТОЧНОСТЬЮ ɛ

1. Метод Ньютона (метод касательных)

В методе Ньютона для нахождения корня используют значения производной. Этот метод основан на замене исходной функции f(x) на каждом шаге поиска касательной, проведенной в этой точке. Пересечение касательной с осью х дает приближенное значение корня.

_{Для решения методом Ньютона в MS} Excel необходимо определиться с тем, чему равно x_n: либо a, либо b. Первую касательную рекомендуется проводить в той точке интервала [a; b], где знаки функции f(x_n) и ее кривизны f”(x_n) совпадают. По расчетным данным х_n = b. Найдем f(x_n) и f’(x_n). Далее рассчитываем шаг h как отношение f(x_n)/f’(x_n). Последующие координаты х_n+1 находим как разность х_n – h. Процесс поиска корней продолжается до тех пор, пока не будет выполнено условие:

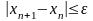
Метод Ньютона требует меньшего числа повторений, чем метод половинного деления. Недостатки метода - необходимость дифференцирования функции f(х), и f ’(x) не должно быть равно нулю.

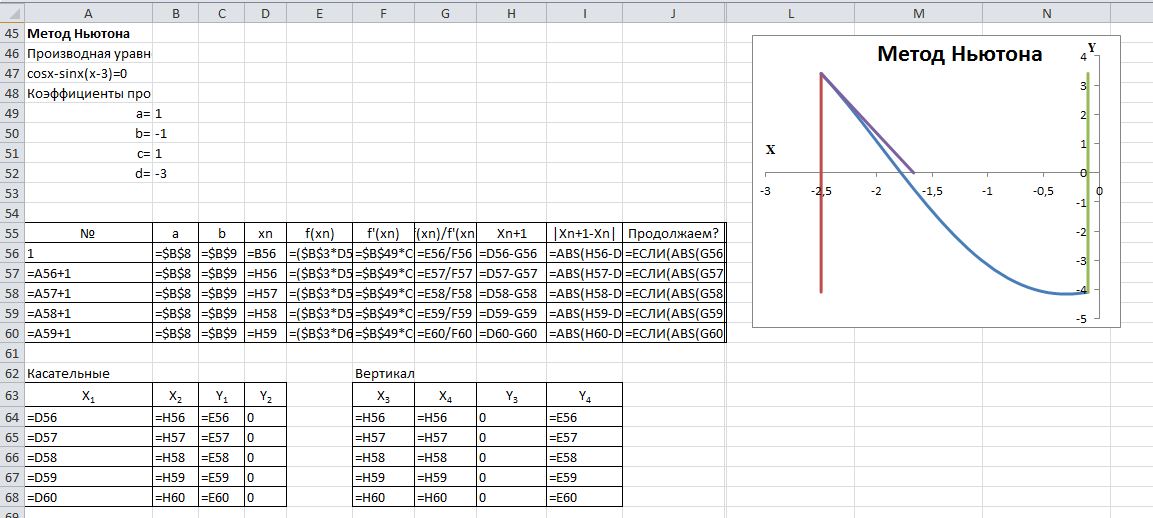
Таблица 1.1 – Вид экрана MS Excel в режиме отображения формул

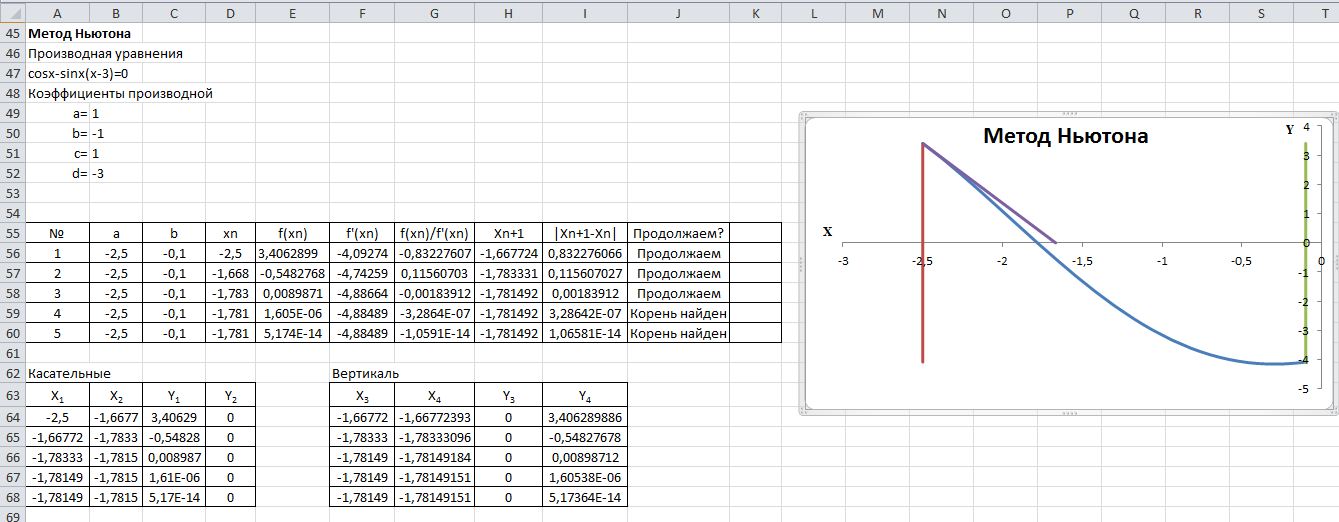
Таблица 1.2 – Вид экрана MS Excel в режиме отображения значений

2. Метод половинного деления

Отрезок [a,b] делят пополам точкой с с=(a+b)/2 и находят значение функции в точке с. Если f(с)=0, то корень уравнения соответствует точке с. Если f(c)±0, то можно сузить диапазон поиска корня: перейти от отрезка [а,b] к отрезку [а,с] или [с,b] в зависимости от знака f(c). Если f(a)∙f(с)<0, то корень находится на отрезке [а,с], и точку с будем считать точкой b; а если f(a)∙f(c)>0, то корень находится на отрезке [с.b], и точку с будем считать точкой а. Каждый такой шаг уменьшает в два раза интервал, в котором находится корень уравнения f(x)=0. После нескольких шагов получится отрезок, длина которого будет меньше или равна числу ɛ, т.е. |a-b|< ɛ. Любая точка такого отрезка, например, один из его концов, подходит в качестве решения поставленной задачи.

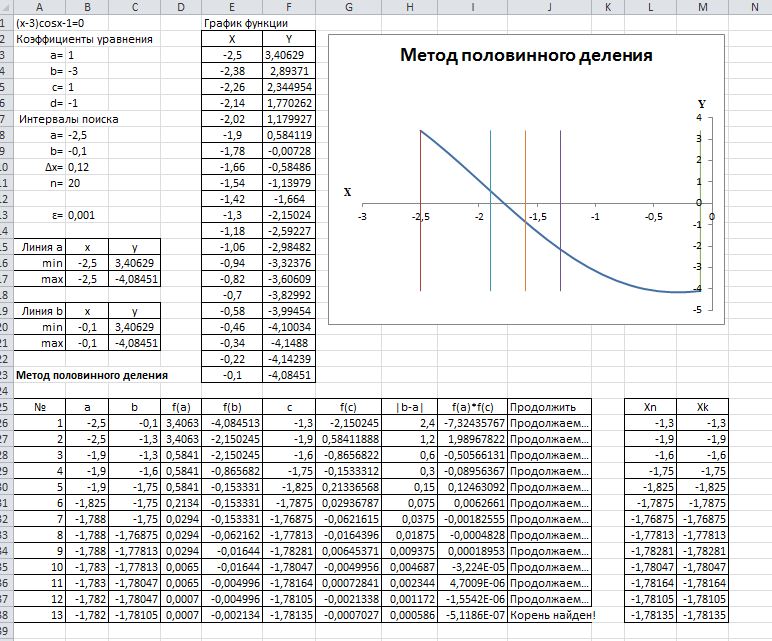
Таблица 1.3 – Вид экрана MS Excel в режиме отображения значений

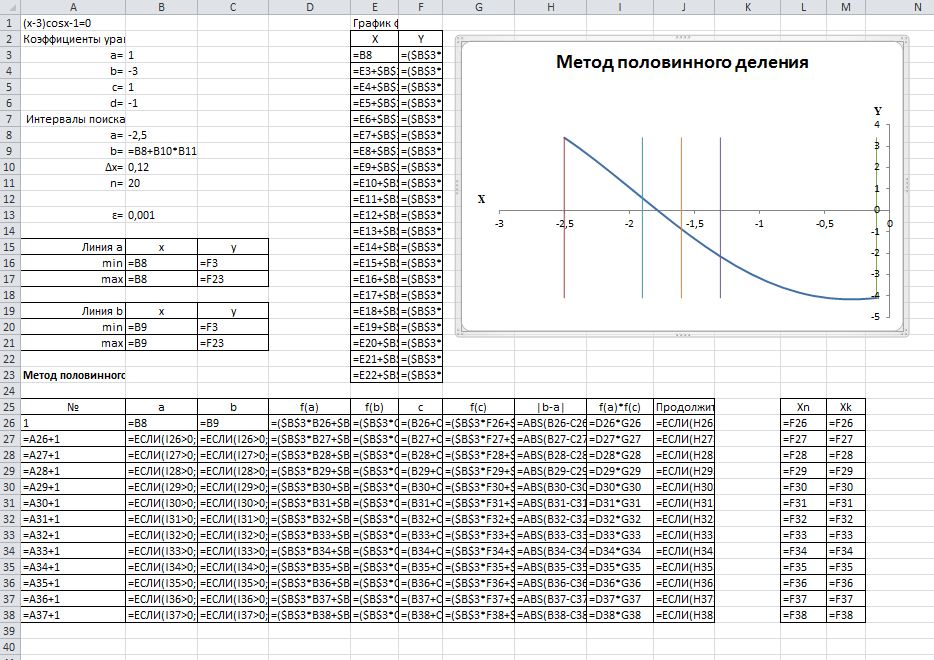
Таблица 1.4 – Вид экрана MS Excel в режиме отображения формул

3. Метод хорд (метод ложного положения)

Метод основан на замене функции, на каждом шаге поиска, хордой, пересечение с которой дает приближенное значение корня. Через точки, соединяющие значения функции f(a) и f(b) на концах отрезка [а,b], проводят прямую, которая пересекает ось х в точке x=a-f(a)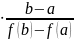 . Значение функции f(х) сравнивается со значениями функций f(а) и f(b) и в дальнейшем используется вместо того из них, с которым оно совпадает по знаку. Если значение f(х) недостаточно близко к нулю, то вся процедура повторяется до тех пор, пока не будет достигнута необходимая степень сходимости ɛ.

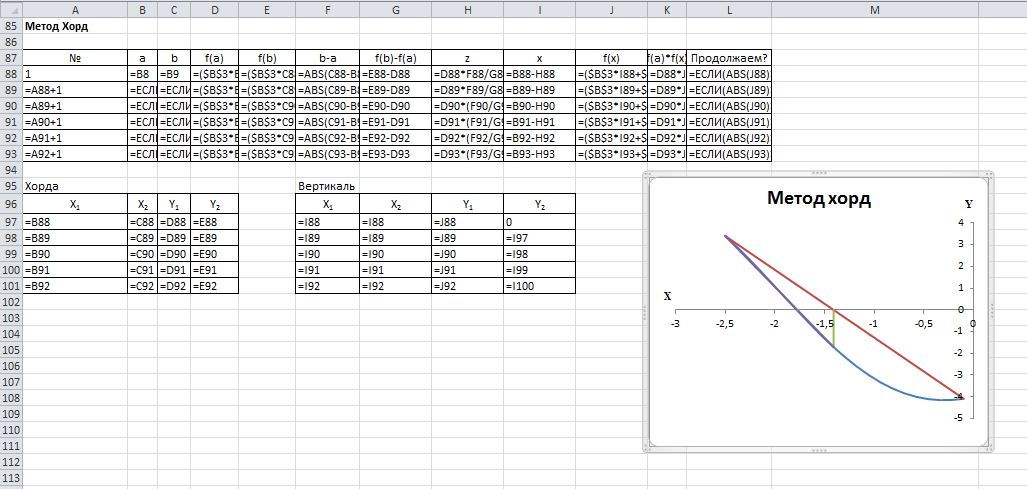
Таблица 1.5 – Вид экрана MS Excel в режиме отображения формул

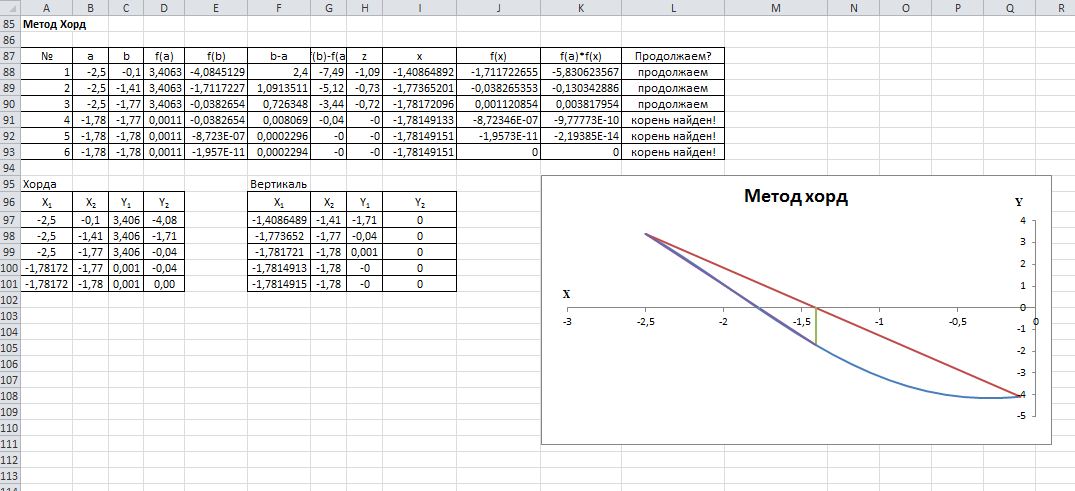
Таблица 1.6 – Вид экрана MS Excel в режиме отображения значений

2 Вычисление определенного интеграла численными методами

Суть всех численных методов интегрирования состоит в приближенном вычислении указанной площади.

2.1 Метод левых прямоугольников

Пусть на отрезке [a,b] задана непрерывная функция у=f(х). Интервал, на котором выполняется интегрирование, [a,b] разбивается на n равных отрезков и криволинейная трапеция S заменяется фигурой, составленной из элементарных прямоугольников с площадями S.

Шаг интегрирования h =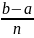

Площадь элементарной фигуры S, = h ∙ у. = h ∙ f(xi).

Таким образом, для вычисления определённого интеграла методом левых прямоугольников достаточно вычислить сумму значений подынтегральной функции, начиная с первого значения и до предпоследнего (в узлах интегрирования) и умножить эту сумму на шаг интегрирования. Преимуществом метода является его простота, недостатком – сравнительно невысокая точность.