4.1.5. Ожидаемая доходность портфеля при использовании только заемных средств

Допустим, инвестор берет кредит в банке и покупает на них более доходный актив. Поскольку используются только заемные деньги, то удельный вес собственных средств равен нулю, а заемных средств – минус единица. Удельный вес покупаемого актива равен единице. Поэтому сумма удельных весов активов в портфеле равна нулю.

Пример 3.

Инвестор занимает в банке 100 тыс. руб. по 10% годовых и приобретает на них рискованный актив А с ожидаемой доходностью 20%. Ожидаемая доходность портфеля равна:

1·20+(-1)·10=10%.

Ожидаемая доходность для инвестора равна бесконечности, поскольку он использовал только заемные средства.

Представленная ситуация имеет только теоретическое значение, поскольку получение кредита связано с определенным обеспечением полученных средств со стороны инвестора, например, залогом имущества. Поэтому ожидаемый результат необходимо оценивать относительно тех средств, которые в этом случае блокируются (выступают залогом).

4.2. Ожидаемый риск портфеля

4.2.1. Ожидаемый риск актива

Приобретая какой-либо актив, инвестор ориентируется не только на значение его ожидаемой доходности, но и на уровень его риска. Ожидаемая доходность выступает как некоторая величина, которую надеется получить инвестор, например 15%. Возможность получения данного результата подтверждается предыдущей динамикой доходности актива. Однако 15% — это только средняя величина. На практике доходность, которую получит инвестор, может оказаться как равной, так и отличной от 15%. Таким образом, риск инвестора состоит в том, что он может получить результат, отличный от ожидаемой доходности. Строго говоря, риск вкладчика заключается в том, что он получит худший, чем ожидаемый результат, т. е. его доходность составит менее 15%. Если фактическая доходность окажется больше 15%, то это плюс для инвестора.

Основополагающими мерами риска финансового актива являются такие показатели как дисперсия и стандартное отклонение доходности. В качестве синонима понятия стандартное отклонение используют также термин «волатильность».

Стандартное отклонение и дисперсия доходности актива говорят степени возможности разброса его фактической доходности вокруг его средней доходности.

Они показывают, в какой степени и с какой вероятностью фактическая доходность актива может отличаться от величины его ожидаемой доходности, то есть средней доходности. Данные параметры учитывают отклонения, как в сторону увеличения, так и уменьшения доходности по сравнению с ожидаемым значением. Как мы отметили выше, фактический риск состоит в том, что фактическая доходность окажется ниже ожидаемой, однако отмеченные параметры используются в качестве меры риска, в первую очередь, в силу простоты их определения.

Данные меры риска можно вычислить на основе прошлых статистических данных доходности актива.

Дисперсия определяется по формуле

, (4.5)

где: r_i — доходность актива в i-м периоде.

n — число периодов наблюдения;

— средняя (ожидаемая) доходность актива; она определяется как средняя арифметическая доходностей актива за периоды наблюдения (см. формулу 4.1).

Если r_i представляет собой доходность за i-й год, то σ² является дисперсией доходности акции в расчете на год. Размерность дисперсии представляет собой квадрат доходности акции. Если в формуле учитывается доходность в процентах, то размерность дисперсии – это процент в квадрате. Показателем такой размерности не всегда удобно пользоваться, поскольку сама доходность акции измеряется в процентах. Поэтому из дисперсии извлекают квадратный корень и получают стандартное отклонение доходности:

, (4.6)

где: σ— стандартное отклонение доходности актива.

Стандартное отклонение измеряется уже в процентах, т.е. в тех же единицах, что и сама доходность.

Если предположить, что при расчете дисперсии и стандартного отклонения учитываются все существующие значения доходности, т.е. всю генеральную совокупность случайной переменной, то полученная по формуле (4.5) дисперсия называется генеральной дисперсией, а стандартное отклонение в формуле (4.6) – генеральным стандартным отклонением. Однако на практике невозможно учесть все фактические значения доходности акции, так как это непрерывная величина. Поэтому оценку данных показателей проводят на основе только части значений, т.е. на основе некоторой выборки данных. Тогда в результате расчета по формуле (4.5) получают выборочную дисперсию.

Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то она будет приводить к систематическим ошибкам, занижая значение генеральной дисперсии. Это происходит потому, что при расчете отклонения его считают не от истинного среднего значения переменной, а от выборочного. Выборочное же среднее значение непосредственно находится в центре выборки и поэтому отклонения от него выборочных данных в среднем меньше, чем от действительного среднего значения переменной в генеральной совокупности. Чтобы скорректировать данную погрешность переходят к так называемой исправленной дисперсии. Она определяется по формуле:

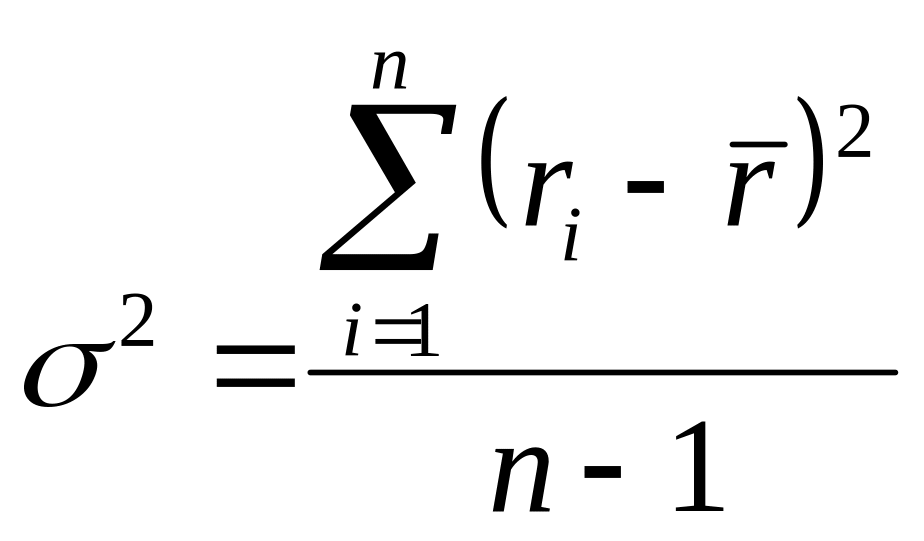. (4.7)

Формула (4.7) от формулы (4.5) только знаменателем. Данная корректировка осуществляется для того, чтобы получить несмещенную оценку генеральной дисперсии. Корректировка является существенной, если оценку дисперсии проводят на основе небольшого количества данных. При большом объеме выборки различие в расчетах будет незначительным. На практике пользуются исправленной дисперсией, если количество наблюдений примерной меньше 30.

Выше мы рассматривали расчет дисперсии и стандартного отклонения, оперируя временным периодом равным одному году. На практике возникает задача определения стандартного отклонения и дисперсии для других временных периодов.

Если имеется значение стандартного отклонения за год, то для определения его значения за один день надо стандартное отклонение в расчете на год разделить на корень квадратный из количества торговых дней в году. В году насчитывается порядка 252 таких дней. Поэтому стандартное отклонение доходности актива за день вычисляется по формуле:

. (4.8)

Если определяется стандартное отклонение за некоторый период t на основе годичного стандартного отклонения, то в общем виде формула имеет следующий вид:

. (4.9)

Если известно стандартное отклонение за один день, то определить его значение в расчете на год можно по формуле:

. (4.10)

Соответственно стандартное отклонение за любой другой период времени определяется по формуле:

. (4.11)

На практике волатильность часто определяется на основе данных о ежедневной доходности акции. Доходность акции за один день определяется по формуле:

, (4.12)

где P_i , P_i-1 – соответственно цена акции в i-й и (i-1)-й день.

На основе полученных данных о ежедневной доходности по формуле стандартного отклонения определяют волатильность в расчете на день. Затем по формуле (4.10) определяют волатильность в расчете на год.

Удобство расчета стандартного отклонения на основе ежедневных данных состоит в том, что можно воспользоваться большим количеством наблюдений.

Доходность актива является случайной величиной и поэтому может принимать различные значения. Если значения переменной изменяются во времени неопределенным (случайным) образом, то говорят, что она следует стохастическому (вероятностному) процессу. Значения случайной переменной могут изменяться дискретно или непрерывно. В первом случае величина переменной изменяется только на определенную (дискретную) величину, во втором – может принимать любые значения в рамках некоторого диапазона.

Значения одной переменной могут изменяться только в определенные моменты времени, другой – в любое время. Поэтому выделяют соответственно дискретный и непрерывный стохастический процессы.

Доходность актива является непрерывной случайной величиной и подчиняется некоторому вероятностному распределению. Наиболее часть в жизни встречается нормальное распределение. Оно возникает в том случае, когда на случайную величину оказывает влияние множество факторов, каждый из которых не имеет определяющего значения. График кривой нормального распределения случайной величины приведен на рис. 4.1.

Рис. 4.1. Кривая нормального распределения

По оси абсцисс представлена область возможных значений случайной величины Х, по оси ординат – плотность распределения вероятности случайной величины Х. В самом общем виде можно дать следующее определение плотности вероятности: это вероятность, приходящаяся на единицу длины отрезка, на котором может принимать значения случайная величина.

Плотность распределения f(x) является одной из форм закона распределения случайной величины, но существует только для непрерывных случайных величин.

График кривой нормального распределения симметричен относительно среднего значения случайной величины, которое называют еще математическим ожиданием случайной величины. На графике значение μ является математическим ожиданием случайной величины Х.

Сама случайная величина может принимать любые положительные и отрицательные значения. Правая и левая ветви графика асимптотически приближаются к оси абсцисс. Вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Если нас интересует вероятность попадания случайной величины в какой либо интервал на оси абсцисс, то она будет равна площади фигуры, ограниченной сверху кривой распределения, снизу – осью абсцисс, по бокам – перпендикулярами, проходящими через границы интервала. Так, вероятность попадания случайной величины Х в интервал (х₁, х₂) равна площади заштрихованной фигуры (см. рис. 4.1). Нормальное распределение полностью определяется двумя характеристиками случайной величины – ее математическим ожиданием и стандартным отклонением.

Стандартное отклонение характеризует степень рассеяния возможных значений случайной величины относительно ее среднего значения. Кроме этого, для нормального распределения оно говорит о вероятности того, что значение случайной величины окажется в некотором интервале. Для нормального распределения существует так называемое правило «трех сигм». Оно говорит о том, что вероятность получить значение случайной величины в диапазоне одного стандартного отклонения от ее средней величины равно 0,683, в диапазоне двух стандартных отклонений – 0,954, трех стандартных отклонений – 0,997.

Проиллюстрируем данное правило на примере.

Пример 4.

Среднее значение доходности акции равно 15.6%, а стандартное отклонение доходности в расчете на год – 12.14%.

Согласно правилу трех сигм, инвестор вправе ожидать, что с вероятностью 0,683 доходность акции через год бут располагаться в интервале 15.612.14%, т.е. от 3.46% до 27.74%. С вероятностью 0,954 этот интервал составит 15.62·12.4%, т.е. от -8.68% до 39.88%. С вероятностью 0,997 интервал возможной доходности будет равен 15.63·12.4% или от -20.82% до 52.02%.

Стандартное отклонение является мерой риска изменения доходности актива. Зная данную величину, инвестор может выбирать между более или менее рискованными бумагами. Например, имеются две акции – А и В. Их средняя доходность одинакова и равна 30%. В то же время, стандартное отклонение в расчете на год акции А равно 10%, акции В – 15%. Это означает, что акция В рискованнее акции А учитывая правило трех сигм, инвестор вправе ожидать, что с вероятностью 0,683 через год он может получить по бумаге А доходность в диапазоне от 20% до 40%, а по бумаге В – от 15% до 45%. Более консервативный вкладчик вберет бумагу А, а более склонный к риску – бумагу В.

Дисперсию как меру риска ввел в теорию портфеля ценных бумаг основоположник современной теории портфеля Г. Марковец. Определенным недостатком данной меры риска является то, что она одинаково учитывает отклонения доходности актива от его средней доходности как в сторону увеличения, так и снижения. В то же время инвестора, купившего финансовый актив, беспокоит именно снижение его доходности. Рост доходности, по сути, не является для него риском.

Дисперсию актива можно рассчитать и на основе прогнозов инвестора в отношении конъюнктуры будущего периода. В этом случае он оценивает возможные сценарии ее развития. На этой основе он прогнозирует значения будущих доходностей актива и задает им субъективные вероятности. Например, инвестор полагает, что будущем периоде актив А принесет доходность r₁ с вероятностью р₁, доходность r₂ с вероятностью р₂ и т.д. доходность r_n с вероятностью р_n. На основе этих данных по формуле (4.2) рассчитывается средняя доходность актива. Далее дисперсия определяется по формуле:

. (4.13)