14. Довірчі інтервали

Окрім точкових оцінок використовують так звані довірчі інтервали: зазначають не одну точку *, а інтервал до якого із заданою ймовірністю належить справжнє значення параметра :

(16)

Число , 0<<1 називається довірчою ймовірністю і характеризує надійність одержаної оцінки: чим ближче  до одиниці, тим надійніша оцінка (зазвичай беруть = 0,9; 0,95 або 0,99).

Величини й називаються довірчими межами. Вони є функціями вибіркових значень = (Х₁, Х₂, …, Х_п), = ( Х₁, Х_2,, …, Х_п), і, отже є випадковими величинами.

Інтервал ( , ) з випадковими межами = (Х₁, Х_2,, …, Х_п), = ( Х₁, Х_2,, …, Х_п), які за довільним припустимим значенням  задовольняють співвідношення (16), називається довірчим інтервалом для невідомого параметра .

Приклади довірчих інтервалів

1. Довірчий інтервал для математичного сподівання a нормальної випадкової величини за відомої дисперсії ² має вигляд

Тут величину u_ визначають за заданою довірчою ймовірністю  за табл. 5 (див. дод. 2).

2. Довірчий інтервал для математичного сподівання a нормальної випадкової величини за невідомої дисперсії ² має вигляд

де оцінку ^* обчислюють за формулою:

(17)

а величину t_ визначають за заданою довірчою ймовірністю  та об’ємом вибірки n за табл. 6 (див. дод. 2).

3. Довірчий інтервал для дисперсії ² нормальної випадкової величини має вигляд

де n – обєм вибірки; ^*– оцінка величини, яку визначають за формулою (17); і – корені рівнянь

(18)

в яких підінтегральна функція p_n–1(x) являє собою щільність розподілу  — квадрат з n–1 степенями вільності.

Рівняння (18) за заданою довірчою імовірністю  розв’язуються за

табл. 7 (див. дод. 2). За визначенням за цією таблицею використовують  = n–1 і за визначенням –  = n–1; .

4. Нехай n – кількість незалежних випробувань, m – кількість наставання події A у кожному окремому випробуванні. Розглянемо випадок, коли n достатньо велике, а значення p не дуже близьке до нуля або одиниці так, що можна використати асимптотику Муавра–Лапласа (див. п.1.6) Довірчий інтервал для p має вигляд р₁< р< р₂, де

u_ – визначають за заданою довірчою ймовірністю  за табл. 5 (див. дод. 2).

Розглянемо окремо випадок m = 0. Нижня довірча межа дорівнює нулеві, верхня – . Аналогічно при m = n нижня і верхня довірчі межі дорівнюють відповідно та одиниці.

15. Статистична перевірка гіпотез

Випадкова величина K, яку застосовують для статистичної перевірки гіпотези, називають критерієм. Іноді терміном “критерій” позначають не тільки випадкову величину K, але і всю процедуру перевірки. При цьому K називають статистикою критерію.

Перевірка гіпотези полягає в тому, що коли спостережене значення критерію належить деякій визначеній множині S, тобто настає подія {K  S}, то основна гіпотеза H₀ відкидається. Така множина S, називається критичною множиною (для гіпотези H₀).

Подія {X  S}, яка полягає в тому, що основна гіпотеза відкидається, коли вона є істинною, називається помилкою першого роду. Подія {K  S}, яка полягає в тому, що основна гіпотеза H₀ приймається, коли вірна одна з альтернативних гіпотез H_, називається помилкою другого роду.

Імовірності P_I і P_II помилок першого і другого роду обчислюють у припущеннях про істинність різних гіпотез – основної H₀ і альтернативної H_, відповідно:

Імовірність помилки другого роду, а також імовірність

(19)

протилежної події пов’язані з конкретною альтернативною гіпотезою H_, тобто можуть залежати від деякого параметра .

Функція (19) параметра , що дорівнює ймовірності відкинути гіпотезу H₀, коли вірна гіпотеза H_, називається функцією потужності критерію.

Правила статистичної перевірки гіпотези

1. Задають малим числом >0, яке називається рівнем значущості критерію; зазвичай  = 0,05; 0,01 або 0,001. Воно характеризує ймовірність помилки першого роду.

2. Визначають критичну множину S за умови виконання нерівності

. (20)

3. Умовою (20) критична множина S визначається неоднозначно. Вибирають ту з можливостей, яка забезпечує мінімум ймовірностей помилки другого роду, або, що те саме, максимум потужності критерію.

4. Проводять випробування та одержують значення критерію. Якщо при цьому настає подія {K  S}, то основна гіпотеза H₀відкидається. У противному разі вважають, що H₀не суперечить експериментальним даним. Результат перевірки гіпотези формулюють: гіпотеза H₀ відкидається (не відкидається) на рівні значущості .

Розглянемо задачу перевірки гіпотези, яка може бути розв’язана за допомогою так званого критерію знаків. Маємо дві -ки незалежних випадкових величин

Вони інтерпретуються як результати виміру деякого показника у об’єктів до "обробки" (1-й рядок) і після "обробки" (2-й рядок). Відповідні реалізації випадкових величин позначимо:

Висувається основна гіпотеза , що "обробка" систематично (у той або інший бік) не впливає на зміну розглянутого показника. Альтернативною гіпотезою є – впливає на зміну. Віднімаючи від верхніх випадкових величин нижні, одержуємо деяку кількість плюсів та деяку кількість мінусів (якщо одержуємо нуль, то відповідну пару відкидаємо).

У якості критерію перевірки гіпотези беремо випадкову величину – кількість плюсів у різницях. Якщо гіпотеза є вірною, то слід очікувати, що

Та вся множина можливих значень (цілі числа від 0 до ) має бінарний розподіл з параметрами , тобто .

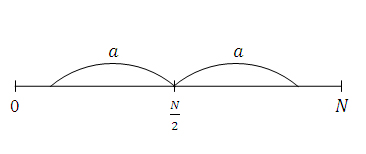
Критичною множиною будемо вважати цілі числа від 0 до та від  до , де величина береться такою, щоб (рівню значущості критерію). Величину можна відшукати з рівняння

В якості критерію перевірки гіпотези можна взяти величину , де – кількість мінусів в різницях. Множина можливих значень – цілі числа від 0 до .

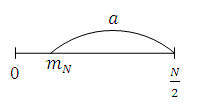
Можна переконатись, що критичною множиною , що відповідає рівню значущості , будуть цілі числа від 0 до , де співпадає з попереднього критерію. Границю критичної області можна знайти за заданими та з таблиці з Додатку 2.

Далі знаходиться реалізація величини по різницях , і якщо попадає в критичну множину , то гіпотеза відкидається, в протилежному випадку вона приймається.