4. Теорема додавання і формула множення ймовірностей

Умовною ймовірністю події А за умови, що сталася подія В, називається число Р(А/В), яке обчислюють за формулою:

Р(А/В)=Р(АВ)/Р(В), Р(В)≠0.

З цього означення випливає формула множення ймовірностей для двох подій

Р(АВ)=Р(А)Р(В/А)=Р(В)Р(А/В).

Ця формула узагальнюється для n подій:

P(A₁ A₂ … A_n)= Р(A₁)Р(A₂/ A₁) Р(A₃/A₁ A₂)… Р(A_n/A₁, A₂, … A_n-1).

Події А і В називаються незалежними, коли виконується співвідношення

Р(А 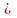В)=Р(А)Р(В).

Теорема. Для довільних подій А та В має місце формула

Р(А В)= Р(А) + Р(В) — Р(АВ),

для n подій – формула

5. Формула повної імовірності, формула Байєса

Сукупність подій Н₁, Н₂,…, Н_n називається повною групою подій, коли

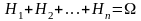і 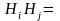, i, j = 1,2, …, n, i j,

де Ω – вірогідна подія;  – неможлива подія.

Теорема 1. Якщо Н₁,Н₂, ..., Н_n - повна група подій та Р(Н _i) ≠ 0,i = 1,2,...n, то для довільної події А виконується рівність (формула повної імовірності)

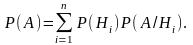
Теорема 2. В умовах теореми 1 для довільної події А, такої, що Р(А) ≠ 0, виконується формула Байєса

1, 2, …, n.

6. Схема незалежних випробувань Бернуллі

Нехай імовірність настання події А при одиничному випробуванні дорівнює р. Випробування повторюється n разів, тобто реалізуються n незалежних випробувань. Імовірність Р_n(m) того, що внаслідок цих n випробувань подія А станеться m разів, визначають за формулою Бернуллі

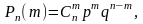m = 0, 1, 2,…, n, (1)

де q=1 - р-імовірність появи протилежної події А в одиночному випробуванні.

Сукупність чисел, визначених за формулою (1), називається біномним розподілом імовірностей.

Значення т = т₀, за якою ймовірність (1) набуває максимального значення, називається найімовірнішим.

Якщо (п+1)р - дробове число, то т₀ набуває єдиного значення

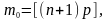
де [...] - символ цілої частини числа. Коли величина (п+1)р - ціла, то т₀ набуває двох значень

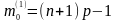та

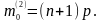
Розглянемо тепер випадок, коли внаслідок кожного з п незалежних випробувань може статися одна з k попарно несумісних подій А₁ А₂, ..., А_к з ймовірностями р₁, р₂, …, р_k відповідно (р₁+ р₂+ …+ р_k=1). Позначимо через m_i кількість тих випробувань, в яких сталася подія А_і і= 1, 2, ..., k. Тоді ймовірність того, що подія А_і настане m₁ разів, подія А₂-т₂ разів, ..., подія А_k-т_k разів, причому т₁ + т₂+... + т_к= п, визначають рівністю

Це поліноміальний розподіл імовірностей. Для великих значень п (десятків, сотень, тисяч) та не малих значень p і q для біномного розподілу використовують такі наближені формули:

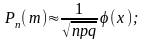(2)

де

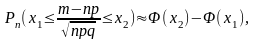(3)

де – функція Лапласа. (4)

За великих значень п та малих значень р (порядку 1/п) використовують наближені формули:

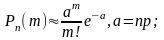(5)

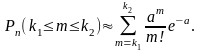(6)

Формула (2) базується на локальній теоремі Муавра-Лапласа, (3) - на інтегральній теоремі Муавра-Лапласа, (5) та (6) - на формулі Пуассона. Асимптотику Муавра-Лапласа (формули (2) та (3) застосовують, якщо прq>9. У противному точніші результати дає асимптотика Пуассона (формули (5) та (6)).

Зауваження 1. Наближена формула (3) справедлива тоді, коли нерівності в ній строгі.

Зауваження 2. Обчислення за формулами (2), (3), (5), (6) виконується з табл. 1 - 4 (див. дод. 2).