Двойственная задача

Чтобы составить модель двойственной задачи, запишем матрицу исходной задачи (1) - (5) в следующем виде:

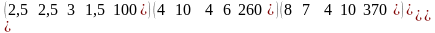(9)

Транспонируем матрицу (9) и получим матрицу (10) двойственной задачи.

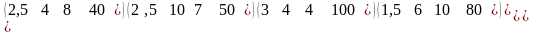
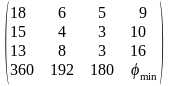. (10)

По исходной матрице (10) запишем модель задачи, двойственной исходной задаче:

φ = 20y₁ + 37y₂ + 30y₃ → min (11)

2y₁ + 3y₂ + 0y₃ 11;

2y₁ + 1y₂ + 1y₃ 6;

4y₁ + 1y₂ + 1y₃ 9; (12)

0y₁ + 2y₂ + 4y₃ 6;

y_i 0 (i =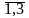 ). (13)

Из теорем двойственности следует, что если решена одна из пары двойственных задач, то одновременно найдено решение и другой задачи. Компоненты оптимального плана этой задачи находятся в строке целевой функции последней симплекс-таблицы решенной задачи.

В предыдущем пункте найден оптимальный план исходной задачи, его компоненты находятся в табл. 5. В f-строке этой же таблицы содержатся и компоненты у_i* оптимального плана двойственной задачи (11) - (13). Выписать компоненты у_i* поможет соответствие между переменными двойственных задач.

Чтобы установить это соответствие, преобразуем ограничения-неравенства (12) в эквивалентные уравнения, вычитая из левых частей дополнительные неотрицательные переменные у₁*, у₂*, у₃*, у₄* равные разностям между левыми и правыми частями этих неравенств. Тогда модель (11) - (13) запишется в виде:

φ = 20y₁ + 37y₂ + 30y₃ → min (11)

2y₁ + 3y₂ + 0y₃ - y₄ 11;

2y₁ + 1y₂ + 1y₃ - y₅ 6;

4y₁ + 1y₂ + 1y₃ – y₆ 9; (12)

0y₁ + 2y₂ + 4y₃ – y₇ 6;

y_i 0 (i =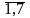 ). (13)

В этой записи переменные у₄, у₅, у₆ ,у₇ являются базисными, а у₁, у₂, у₃ - свободными. В исходной задаче (6) - (8) переменные x₁, x₂, x_3, x₄являются свободными, а x₅, x₆, x₇ - базисными. Сопоставим базисным переменным одной задачи свободные переменные другой и наоборот, т.е.

СП БП

x₁ x₂ x₃ x₄ x₅ x₆ x₇

у₄ у₅ у₆ у₇ у₁ у₂ у₃ (14)

БП СП

Воспользуемся соответствием (14) для нахождения компонентов оптимального плана двойственной задачи. Находим их в табл. 5 в f-строке

		x1	x2	x3	x4	x5	х6	х7
f	810/5	0	0	1/5	0	8/5	13/5	1/5
		у4	у5	у6	у7	у1	у2	у3

Получим оптимальный план двойственной задачи:

Y* = (8/5; 13/5; 1/5; 0; 0; 1/5;0). (15)

Как следует из теорем двойственности, экстремальные значения функций разрешимых двойственных задач совпадают:

f_max = φ_min = 810/5.

Величины y₁* = 8/5, y₂* = 13/5 и y₃* = 1/5 ден. ед. являются теневыми ценами на ресурсы S₁, S₂, S₃ соответственно и в данном случае служат мерой их дефицитности.

Как следует из оптимального плана (15) двойственной задачи Ресурс S₂ является наиболее дефицитным (y₂* = 13/5), ресурс S₁ менее дефицитным (y₁* = 1/5).

Решение транспортной задачи методом потенциалов.

В пункте Аi (i = 1,2,3) находится однородная про­дукция в количестве ai единиц. Себестоимость единицы продукции в пункте Аi равна ci . Готовая продукция поставляется в пункт Вj (j = 1,2,3,4), потребности которого составляют bj единиц. Стоимость сij перевозки единицы продукции из пункта Ai в пункт Bj известна. Требуется:

составить экономико-математическую модель задачи, позволяющую найти план перевозки готовой продукции из пункта Аi производства в пункт В; потребления при полном удовлетворении спроса на продукцию в этих пунктах, обеспечивающего минимальные суммарные затраты, вызванные производством и доставкой продукции;

найти оптимальный план перевозки продукции при дополнительном условии, что продукция пункта Аk, в котором себестоимость ее производства наименьшая, должна быть распределена полностью;

вычислить величину f min минимальных суммарных затрат на производство и доставку продукции;

назвать пункты, в которых остается нераспределенная продукция, и указать объемы такой продукции

Все необходимые числовые данные приведены в табл. 2.

Таблица 2

Параметр		Вариант
		8
a1		360
a2		440
a3		520
c1		2
c2		3
c3		5
b1		240
b2		480
b3		120
b4		320
c11		5
c12	8
c13	11
c14	7
c21	11
c22	6
c23	9
c24	7
c31	5
c32	7
c33	4
c34	2