БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Международный институт дистанционного образования

Контрольная работа

по дисциплине: «Экономико-математические методы и модели»

Выполнил: Тратата

Нананананананна!

Ст. гр. Ыч Ыч!

Проверил: Голиков

Владимир Федорович

Минск 2013 План

1. Решение задачи линейного программирования симплекс-методом;

2. Решение транспортной задачи методом потенциалов;

3. Решение задачи методом наименьших квадратов.

Решение задачи линейного программирования симплекс-методом.

На предприятии выпускают n видов продукции 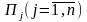. При ее изготовлении используются ресурсы P1, P2 и P3. Размеры допустимых затрат ресурсов ограничены соответственно величинами b1, b2 и b3. Расход ресурса i-го (i = 1, 2, 3) вида на единицу продукции j-го вида составляет aij ден. ед. Це­на единицы продукции j-го вида равна cj ден. ед.

Требуется:

- составить экономико-математическую модель задачи, позволяющую найти сбалансированный план выпуска про­дукции, обеспечивающий предприятию максимальный до­ход;

- найти оптимальный план выпуска продукции по видам (дать содержательный ответ, раскрыв экономический смысл всех переменных, приведенных в решении задачи);

Все необходимые числовые данные приведены в табл. 1

Таблица 1

Параметр	Вариант
	8
n	4
b1	100
b2	260
b3	370
a11	2,55
a12	2,5
a13	3
a14	1,5
a21	4
a22	10
a23	4
a24	6
a31	8
a32	7
a33	4
a34	10
c1	40
c2	50
c3	100
c4	80

Решение.

Исходя из условия задачи имеем:

n = 4; B = 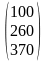; A =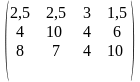 ; C= (40 50 100 80).

Обозначим через x1, x2, x3, x4 количество единиц продукции соответственно P1, P2, P3, P4 планируемой к выпуску, а через f - величину дохода от реализации этой продукции. Тогда, учитывая цену единицы продукции P1, равную 40 ден. ед., единицы P2 - 50 ден. ед., единицы P3- 100 ден. ед., единицы единицы P4- 80 ден. ед., запишем суммарную величину дохода - целевую функцию - в следующем виде:

f = 40x₁ + 50x₂ + 100x₃+80x₄ (1)

Переменные х₁, х₂, х_3, х₄ должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении предприятия ресурсов. Так, затраты ресурса Р₁ на выполнение плана (х₁, х₂, х_3, х₄) составят

2,5x₁ + 2,5x₂ + 3x₃ +1,5x₄ единиц,

где 2,5х₁ - затраты ресурса Р₁ на выпуск x₁ единицы продукции П₁; 2,5х₂ - на выпуск единицы продукции Р₂; 3х₃ - на выпуск единицы продукции Р₃; 1,5х₄ - на выпуск единицы продукции Р₄. Указанная сумма не может превышать имеющийся запас Р₁ в 100 единиц, т.е.

2,5x₁ + 2,5x₂ + 3x₃ +1,5x₄  100 (2)

Аналогично получаем ограничения по расходу ресурсов Р₂, Р₃:

4x₁ + 10x₂ + 4x₃ +6x₄  260 (3)

8x₁ + 7x₂ + 4x₃ +10x₄  370 (4)

По смыслу задачи переменные х₁, х₂, х₃, х₄ не могут выражаться отрицательными числами, т.е.

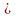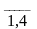x_j 0 (j= ) (5)

Соотношения (1) - (5) образуют экономико-математическую модель данной задачи. Итак, математически задача сводится к нахождению числовых значений х₁*, х₂*, х₃*, х₄* переменных х₁, х₂, х₃, х₄ удовлетворяющих линейным неравенствам (2) - (5) и доставляющих максимум линейной функции (1).

Приведем модель задачи к канонической форме, преобразовать неравенства в эквивалентные уравнения. Для этого введем в левые части неравенств дополнительные (балансовые) неотрицательные переменные x₅, x₆, х₇. В результате получим:

f = 40x₁ + 50x₂ + 100x₃ +80x₄→ max (6)

2,5x₁ + 2,5x₂ + 3x₃ +1,5x₄ +x₅= 100

4x₁ + 10x₂ + 4x₃ +6x₄ + x₆= 260 (7)

8x₁ + 7x₂ + 4x₃ +10x₄ = 370

x_j  0 (j =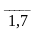 ) (8)

Экономический смысл переменных х₅, х₆ , х₇ - возможные остатки ресурсов Р₁, Р₂, Р₃ , Р₄ соответственно (резервы).