8.3. Аналіз лінійних кіл синусоїдального струму

Гармонічна напруга частотою  спричиняє появу в лінійних елементах кіл гармонічних струмів тієї ж частоти. Тому задача аналізу лінійних кіл змінного синусоїдного струму зводиться до визначення амплітуд і початкових фаз струмів в елементах і напруг на них. Застосувавши співвідношення (8.1), на основі законів Кірхгофа записують диференціальні рівняння, що відображають взаємозв'язок струмів і напруг для кола. Однак розв’язки систем диференціальних рівнянь, які отримуються в багатьох випадках пов'язані зі значними труднощами. Тому для розрахунків застосовують метод комплексних амплітуд. При його використанні з'являється можливість систему диференціальних рівнянь замінити системою алгебраїчних рівнянь, рішення якої набагато простіше, ніж першої.

Взаємозв'язки комплексних амплітуд струму і напруги для резистивних, індуктивних і ємнісних елементів виражаються наступними співвідношеннями;

.

Замість комплексних амплітуд напруг і струмів можна записувати комплекси їх діючих значень.

Як приклад розрахуємо струми у вітках паралельного контуру І_1m І_2m (рис. 8.7). загальний струм в колі І_m i опір контуру Z_кон.

Для струмів віток контуру

;

За правилом Кірхгофа

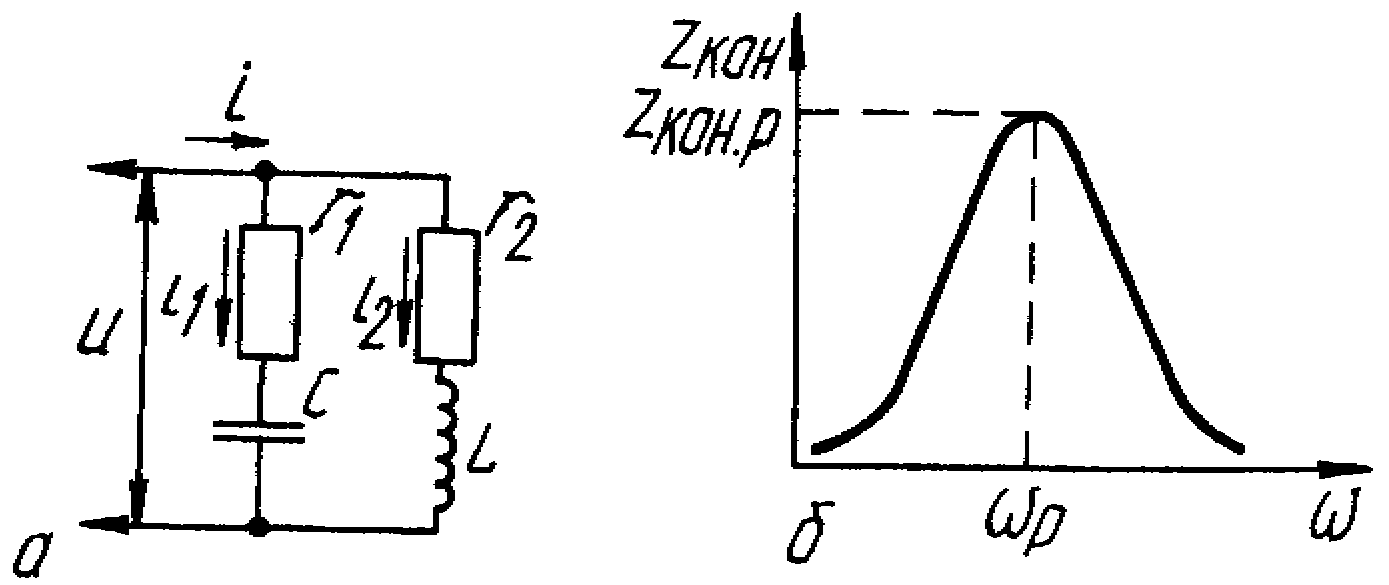
Рис.8.7. Схема паралельного контуру (а) і графік залежності опору контуру від частоти (б)

Опір паралельного, контуру _кон визначається як частка від ділення комплексної амплітуди напруги _m на контурі на комплексну амплітуду загального струму кола _m:

(8.3)

Для радіотехнічних контурів, як правило, виконуються співвідношення: r₁<<1/C, r₂<<L. Проведемо для таких контурів заміну r₁+r₂ на r і отримаємо

(8.4)

На частоті _р, що являється резонансною, L_р=1/(С_р)=0. Опір контуру стає активним і рівним Z_кон.р=L/(Cr) Резонансна частота пов'язана з параметрами контуру . З метою отримання зручного для розрахунків радіотехнічних контурів виразу перетворюємо співвідношення (8.4):

При значеннях  , близьких до _р тобто при , знайдемо

Тому

(8.5)

Підставляючи (8.5) в (8.4), запишемо

Залежність опору паралельного контуру від частоти (рис. 8.7 ,б) визначається виразом

На резонансній частоті опір паралельного контуру є максимальним.

8.4. Лінійні чотириполюсники і їх характеристики

У багатьох випадках електричне коло або його частину подають у вигляді абстрактного пристрою з двома вхідними і двома вихідними затисками. Такий пристрій називають чотириполюсником. Передбачається, що до вхідних затисків підводиться напруга u₁(t) і в результаті на виході чотириполюсника появляється напруга u₂(t). Представлені інтегруюче і диференціююче кола. (див. рис. 8.4, а і 8.5, а) цілком можна трактувати як чотириполюсники.

Чотириполюсник, що включає тільки лінійні елементи, називається лінійним. При вмісті хоч би одного нелінійного елемента чотириполюсник вважаються нелінійним, а при наявності або відсутності джерел струму або е.р.с. - відповідно активним або пасивним. Гармонічна напруга, яка підводиться до вхідних затисків лінійного чотириполюсника u₁=U_1msin(t+₁) приводить до появи гармонічних струмів в його елементах і гармонічної напруги u₂=U_2msin(t+₂) на його виході. Передавальні властивості лінійного чотириполюсника при гармонічних напругах характеризуються комплексним коефіцієнтом передачі, що є відношенням комплексних амплітуд вихідної і вхідної напруг:

Модуль комплексного коефіцієнта передачі K_u() визначає відношення амплітуд напруг, а аргумент - різницю фаз напруг на виході і вході.

У загальному випадку величини () K_u() і arg () залежать від частоти напруги . Частотну залежність K_u() виражає амплітудно-частотна характеристика (АЧХ) чотириполюсника, а частотну залежність arg () - фазочастотна характеристика (ФЧХ) чотириполюсника. Ці залежності представляють графічно.

Смугу частот вхідної напруги, в межах якої на вихід чотириполюсника передається не менш половини потужності, що підводиться до нього, називають смугою пропускання чотириполюсника. Оскільки потужність пропорційна квадрату амплітуди напруги, в межах смуги пропускання коефіцієнт передачі чотириполюсника по напрузі К_u() повинен мати значення не менше за 1/ 0,707 від свого максимального значення:

Частота _гр, при якій , називаєтся граничною частотою смуги пропускання.

Визначимо комплексний коефіцієнт передачі чотириполюсника у вигляді найпростішого RC-кола, в якому вихідна напруга знімається з конденсатора (див. рис. 8.4, а):

де =arctg(-RC).

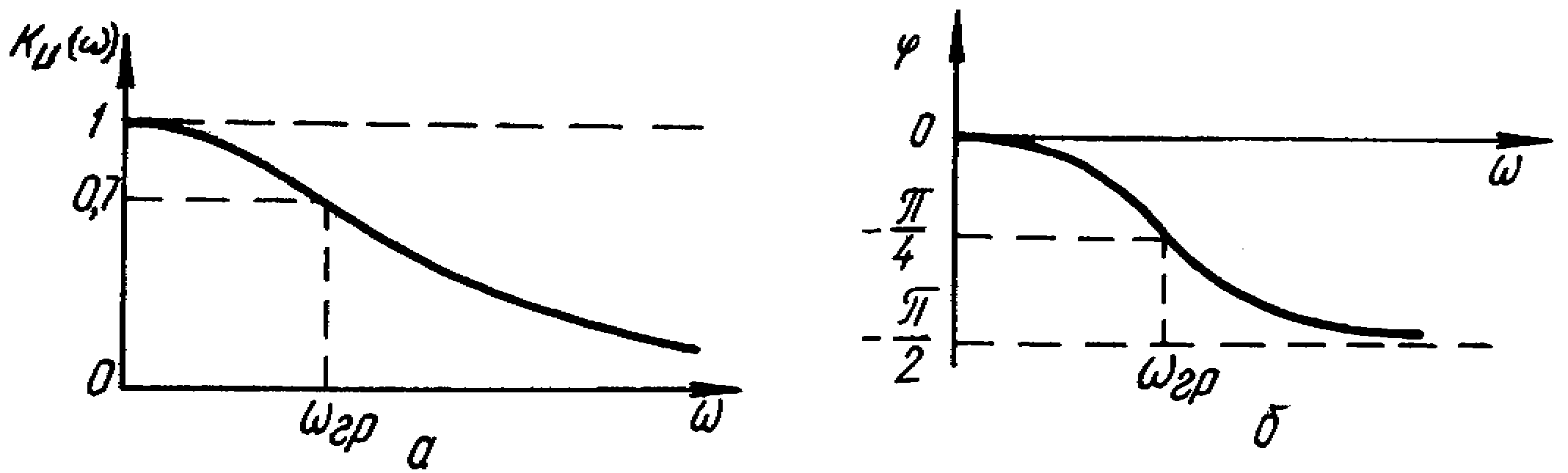
Рис. 8.8. Амплітудно-частотна (а) і фазочастотна (б) характеристики чотириполюсника резистор - конденсатор

Співвідношення K_u()= визначає вигляд амплітудно - частотної (рис. 8.8, а), а вираз =arctg(-RC) - вигляд фазочастотної характеристик (рис. 8.8, б). На частоті =0 K_u()=1, а при  K_u() , тобто по мірі зростання частоти вхідної напруги амплітуда напруги на виході зменшується. Коло, що володіє такими властивостями, називають фільтром нижніх частот.

Знайдемо граничну частоту фільтра. Відповідно до визначення граничної частоти запишемо

Дана рівність має місце при або при

Вихідна напруга відстає по фазі відносно вхідної на кут . При 0 0, а при  /2.

Проведемо подібні розрахунки для чотириполюсника, в якому першим елементом є конденсатор, а другим - резистор (див. рис. 8.5, а). Для комплексного коефіцієнта передачі

Рис. 8.9. Амплітудно-частотна (а) і фазочастотна (б) характеристики чотириполюсника конденсатор - резистор

На основі отриманих співвідношень побудуємо амплітудно-частотну (рис. 8.9, а) і фазочастотну (рис. 8.9, б) характеристики. На високих частотах амплітуда вихідної напруги мало відрізняється від амплітуди напруги на вході, на низьких частотах спостерігається значне її зменшення.

Розглянутий чотириполюсник може бути використаний як фільтр верхніх частот; гранична частота цього фільтра визначається за формулою, аналогічно рівнянню для знаходження _гр фільтра нижніх частот:

Напруга и₂ випереджає по фазі напругу u₁. Фазовий зсув між ними в залежності від частоти може змінюватися в межах від 0 при 0 до  при .