МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

КРИВОРІЗЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

Кафедра обліку, аудиту і фінансового аналізу

Методичні вказівки

до виконання індивідуальної роботи

з дисципліни «Статистика»

для студентів економічних спеціальностей

КРИВий РІГ

2013

Укладач:

• к.е.н., доцент кафедри ОАФА Адамовська Вікторія Сергіївна.

Відповідальний за випуск:

доктор економічних наук, професор Нусінов В.Я.

Методичні вказівки до виконання індивідуальної роботи з дисципліни „Статистика” для студентів економічних спеціальностей

Розглянуто

на засіданні кафедри

обліку, аудиту і

фінансового аналізу

Протокол № 1

від 29.08.20 р.

Схвалено

на вченій раді

інженерно-економічного факультету

Протокол № __

від ____________ 20 р.

Передмова

Індивідуальна робота з дисципліни “Статистика” сприяє не тільки поглибленому вивченні студентами важливих методологічних питань статистики, але й набуттю практичних навичок в агрегуванні інформації, розрахунках узагальнюючих статистичних показників і проведенні порівняльного аналізу; аналізі закономірностей розподілу та динаміки, аналізі взаємозв’язків.

При самостійному вивченні учбового матеріалу необхідно керуватись програмою дисципліни та рекомендованою літературою.

Індивідуальна робота включає вісім задач. До кожної з неї викладені методичні вказівки.

Варіант завдання індивідуальної роботи для студентів видається викладачем.

Індивідуальна робота оформляється в шкільному зошиті, або на папері формату А4 і здається на кафедру. Номер варіанта завдання та його модифікація вказується на початку роботи.

Перед рішенням кожної задачі наводиться її умова. Розв’язок задач наводиться в послідовності завдання (№1-№8).

Незарахована індивідуальна робота повертається для доробки.

І. Методичні вказівки до виконання індивідуальної роботи.

Для рішення задачі №1 необхідно вивчити тему “Зведення та групування статистичних даних”. Групування – це розподіл елементів сукупності на групи та підгрупи за істотними для них ознаками. Виділяють структурні, типологічні, та аналітичні групування.

За допомогою аналітичного групування виявляють взаємозв’язки між двома ознаками, з яких одна представляє результат, а інша – фактор, що впливає на результат.

Аналітичні групування здійснюють за факторною ознакою.

Первинний ряд наглядно не дає уявлення про розподіл одиниць за величиною ознаки в сукупності. Тому першим кроком для упорядкування первинного ряду є його ранжування, тобто розміщення усіх варіант ряду за напрямком зростання чи спаду. Ранжований ряд даних дозволяє виявити мінімальне і максимальне значення ознаки.

Потім визначають ширину інтервалу, яка при заданій кількості груп і рівних інтервалах дорівнює:

де і - відповідно максимальне та мінімальне значення ознаки;

- число груп.

Точність ширини інтервалу повинна визначатись у відповідності до ступеня точності даних спостереження:

– якщо дані спостереження подані з точністю до 0,1, то величина інтервалу округляється до цілих із десятими.

Ширина інтервалу дозволяє визначити межі усіх інтервалів ряду розподілу.

В кожен інтервал включають варіанти, числові значення яких більше або рівні нижній межі і менші або рівні верхній межі цього інтервалу.

В кожній групі визначають кількість підприємств, обсяг результативної та факторної ознаки, їх середній рівень.

Рішення задачі повинно бути оформленим у вигляді робочої таблиці (по усій сукупності), таблиці кінцевого ряду розподілу та його гістограми.

При побудові гістограми на осі абсцис відповідно до прийнятого масштабу відкладають нижню і верхню межі інтервалів, а по осі ординат – частоти. Потім для кожного інтервалу будують прямокутник основою якого є відрізок на осі абсцис, а висота якого пропорційна частоті інтервалу.

В кінці рішення задачі здійснюють аналіз результатів і роблять висновки.

За наявністю зв’язку між факторною і результативною ознаками групові середні від групи до групи поступово змінюються – збільшуються чи зменшуються. Це свідчить про наявність зв’язку.

Для розв’язання задачі №2 необхідно:

1. засвоїти методи розрахунків в інтервальному ряді розподілу середніх величин, абсолютних та відносних показників варіації;

2. усвідомити поняття генеральної і вибіркової сукупності, частки вибірки у генеральній сукупності 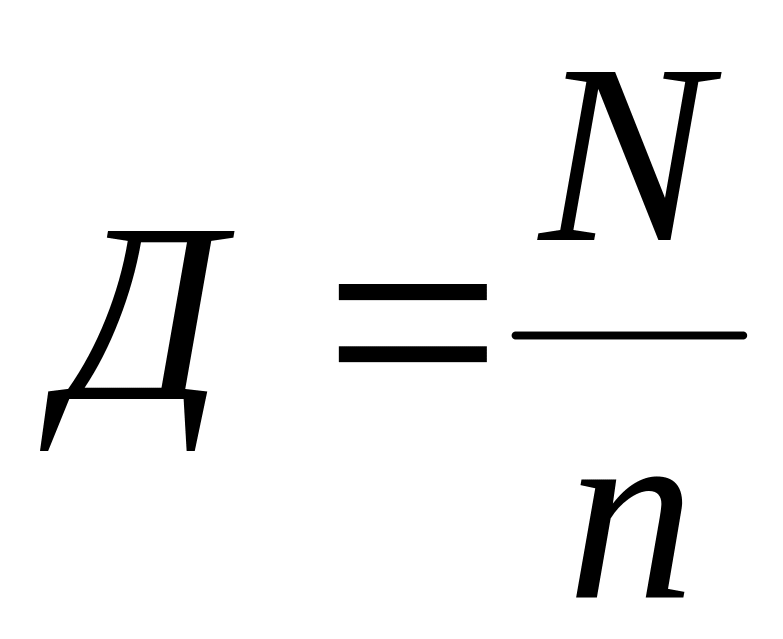та вибіркової частки, якій притаманна певна ознака ( );

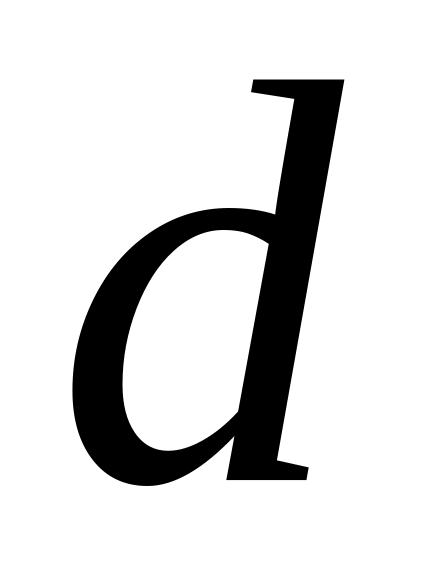3. оволодіти методами розрахунків граничної помилки параметрів вибіркової сукупності.

Для визначення середньої та показників варіації ознаки х за даними інтервального ряду складають табл. 1.1.

Табл. 1.1.

Розрахункові дані для рішення задачі №2.

Групи підприємств за вартістю основних фондів	Кількість підприємств
1	2	3	4	5	6	7	8
В цілому по сукупності		–			–	–

Перші дві графи таблиці заповнюються за даними інтервального ряду розподілу задачі №1.

Розрахунок середньої за згрупованими даними носить умовний характер, так як ґрунтується на припущенні, що в межах інтервалу індивідуальні значення ознаки розподіляються рівномірно.

Середню визначають за формулою середньої арифметичної зваженої:

,

де: - середнє значення ознаки ої групи, для кожної групи визначається як середнє значення інтервалу, тобто як півсума двох його меж;

частота -ої групи;

- число значень ознаки по сукупності в цілому.

Для характеристики варіації ознаки Х необхідно обчислити дисперсію, середнє квадратичне відхилення та квадратичний коефіцієнт варіації.

Дисперсія – це середній квадрат відхилень від середньої. Для згрупованих даних

,

або

Середнє квадратичне відхилення – це корінь квадратний із дисперсії

Коефіцієнти варіації розраховують як відношення абсолютних характеристик варіації до характеристики центру розподілу. Квадратичний коефіцієнт варіації обчислюють за формулою

Вважають, що сукупність є однорідною, а середня типовою, коли коефіцієнт варіації не перевищує 33%.

Вибіркова сукупність, яка обстежується є частиною генеральної сукупності з якої проводиться відбір ознак для спостереження.

Між характеристиками вибіркової сукупності і характеристиками генеральної сукупності, як правило існують деякі розходження, які називають помилкою вибірки.

Розмір граничної помилки вибірки залежить від варіації ознаки , обсяг вибірки та її частини у генеральній сукупності , від прийнятого рівня ймовірності:

де квантиль нормального розподілу, довірче число (коефіцієнт довіри), який вказує як співвідносяться гранична і стандартна помилки вибірки для прийнятого рівня ймовірності;

- стандартна помилка вибірки, середнє квадратичне відхилення вибіркових оцінок від значень параметра генеральної сукупності.

В економічних розрахунках рекомендується використовувати довірчу ймовірність 1- або для яких квантиль відповідно складає 1.96 та 2.00.(додаток 1)

У теорії вибіркового методу розглядається два способи відбору: повторний і безповторний. При повторному відборі за схемою кулі, що повертається імовірність попасти в вибірку однакова для всіх елементів сукупності. При безповторному відборі за схемою кулі, що не повертається відібрана одиниця не повертається назад і ймовірність відбору окремих елементів весь час змінюється.

Використання випадкової повторної вибірки в практиці обмежено. Тому в задачі визначають середню квадратичну помилку випадкової безповторної вибірки за формулою:

де - обсяг вибірки;

- обсяг генеральної сукупності.

Довірчі межі генеральної середньої та частки визначають наступним чином:

де гранична помилка вибіркової середньої;

- генеральна частка;

d - вибіркова частка;

гранична помилка вибіркової частки.

Моду розраховують за формулою

де нижня межа модального інтервалу;

h-ширина модального інтервалу;

відповідно частота модального, передмодального і післямодального інтервалів;

Медіану в інтервальному ряду знаходять за наступною формулою:

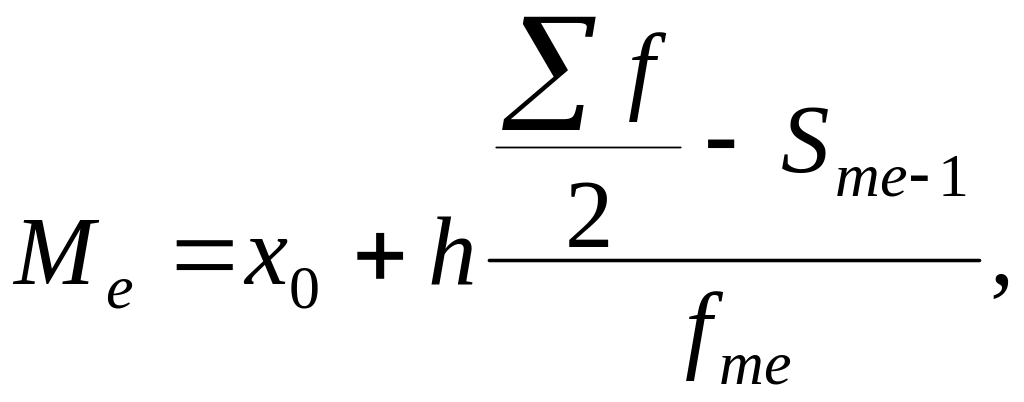
де відповідно нижня межа і ширина медіанного інтервалу;

сума накопичених частот в передмедіанному інтервалі;

частота медіанного інтервалу.

В задачі №3 передусім необхідно розрахувати абсолютні та відносні характеристики ряду динаміки.

Динамічний ряд - це послідовність чисел, які характеризують зміну того чи іншого соціально-економічного явища. Для динамічного ряду характерні перелік хронологічних дат або інтервалів часу і конкретні значення відповідних статистичних показників, які називають рівнями ряду.

Розрахунок характеристик рядів динаміки ґрунтується на зіставленні рівнів ряду :

Абсолютний приріст відображає абсолютну швидкість зміни рівнів ряду; розраховується як різниця рівнів динамічного ряду:

Ланцюгові базисні

Коефіцієнт зростання розраховується як відношення рівнів ряду:

Ланцюгові базисні

Темп приросту показує на скільки процентів рівень більше (менше) рівня, взятого за базу порівняння:

ланцюгові

базисні

Абсолютне значення 1% приросту показує, чого вартий один процент приросту, розраховується як співвідношення абсолютного приросту і темпу приросту:

для ланцюгових темпів приросту

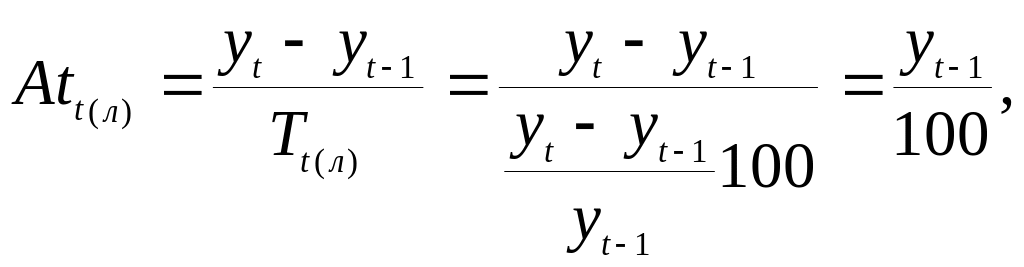
для базисних темпів приросту

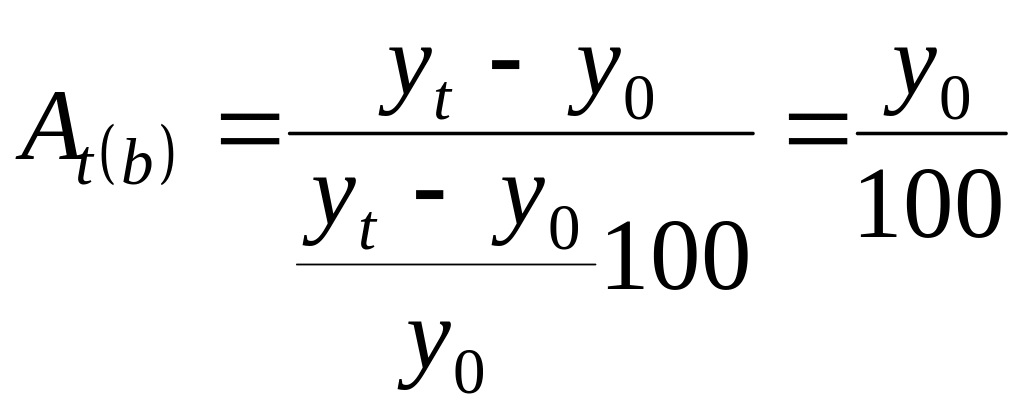
Середній абсолютний приріст розраховується як середня арифметична проста з ланцюгових абсолютних приростів:

Середній коефіцієнт зростання розраховується за формулою середньої геометричної

де n – число ланцюгових коефіцієнтів зростання.

Другим питанням рішення задачі №3 є визначення тенденції зростання обсягу виробництва, продукції за допомогою лінійного тренду.

Тенденція це основний напрямок розвитку її описують функцією

де t = 0,1,2,…,n – зміни часу;

теоретичні рівні ряду.

При відносно стабільних абсолютних приростах використовують лінійний тренд . Параметр характеризує середній абсолютний приріст, а параметр а – теоретичне значення рівня при t=0

Складають систему нормальних рівнянь:

Для розрахунку параметрів трендового рівняння в його довірчих межах та коефіцієнта автокореляції заповнюють табл.1.2.

Таблиця 1.2.

Розрахункові данні для розв’язування задачі №3.

Рік	Обсяг вироб­ництва yt	t	t2	ytt	Yt	yt-Yt	(yt-Yt)2	Et+1		Et Et+1
1	2	3	4	5	6	7	8	9		10
1		-3
2		-2
3		-1
4		0
5		1
6		2
7		3
Разом	yt	0	t2	yt t	Yt	–	(yt-Yt)2		–	Et Et+1

Якщо початок відліку часу (t=0) перенести в середину ряду, то t =0, а отже

,

В трендовому рівнянні параметр - показує середньорічний обсяг виробництва, а параметр - щорічний абсолютний приріст обсягу виробництва.

Для оцінки автокореляції залишкових величин розраховують коефіцієнт автокореляції за формулою:

,

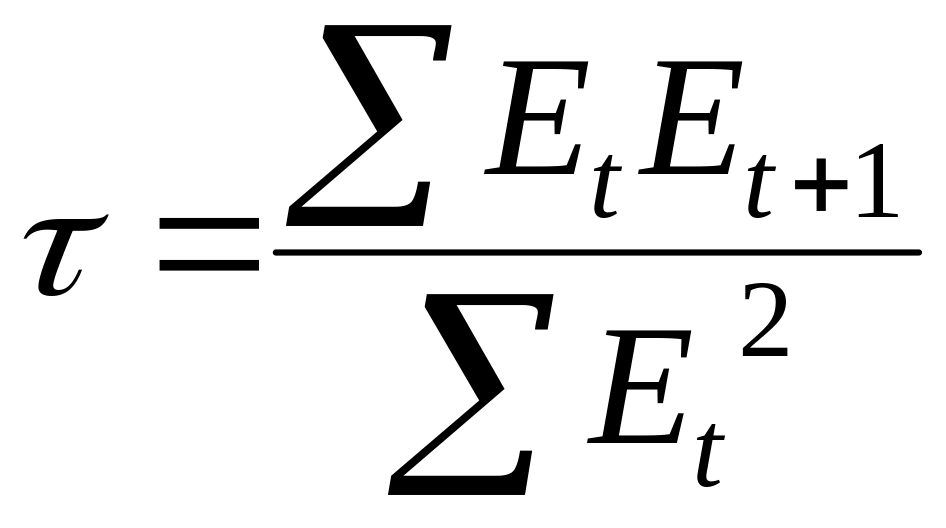та порівнюють його з критичним значенням (додаток 5).

За умови, що комплекс причин, які формують тенденцію, ближчим часом не зміниться, можна продовжити тенденцію за межі динамічного ряду і дати точковий прогноз в майбутньому. Для цього необхідно розрахувати теоритичні значення підставивши в трендове рівняння майбутні значення фактору часу.

Інтервальна оцінка прогнозу, тобто його довірчі межі визначаються для ймовірності за формулою

,

де - помилка прогнозу, t- довірче число для прийнятого рівня імовірності; V – період упередження.

Помилка прогнозу розраховується за формулою:

де оцінка залишкової дисперсії;

m- число параметрів рівняння.

Критичні значення t- критерію Стьюдента для імовірності 1-=0,95 та ступенів вільності K=n-m наведенні в додатку 2.

В задачі №4 необхідно перерахувати в умовно-натуральні одиниці кілька різновидів металопродукції, або видів палива за допомогою коефіцієнтів - сумірників. Коефіцієнти перерахунку в умовні одиниці металопродукції наведено в завданні, а для перерахунку обсягу видобутку палива в умовні одиниці розраховують калорійні коефіцієнти відношенням теплотворної спроможності певного палива до теплотворної спроможності 7000 Дж, прийнятої за еталон.

Виходячи з обсягів виробництва металопродукції в умовно-натуральному вираженні визначають виконання плану в цілому по підприємству (Квn);

де відповідно обсяг виробництва продукції фактично та за планом.

Аналогічно визначають динаміку обсягів видобутку палива:

де відповідно обсяги видобутку палива у звітному і базовому періодах.

Структуру виробництва продукції фактично та за планом і видобутку палива в базовому та плановому періодах визначають також за обсягами в умовно-натуральних одиницях.

Зміна часток окремих складових частин сукупності – це наслідок структурних зрушень. Структурні зрушення оцінюють за допомогою абсолютних і відносних характеристик динаміки.

Абсолютний приріст -ї частки в процентних пунктах розраховують за формулою:

А коефіцієнт зростання -ї частки:

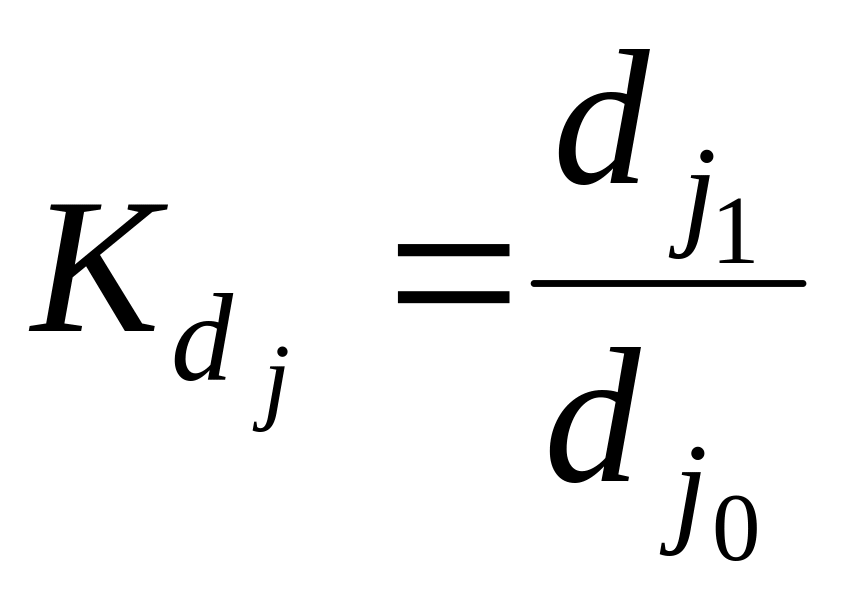
Як узагальнюючі характеристики інтенсивності структурних зрушень застосовують лінійний і квадратичний коефіцієнти, які обчислюють на основі абсолютних приростів часток

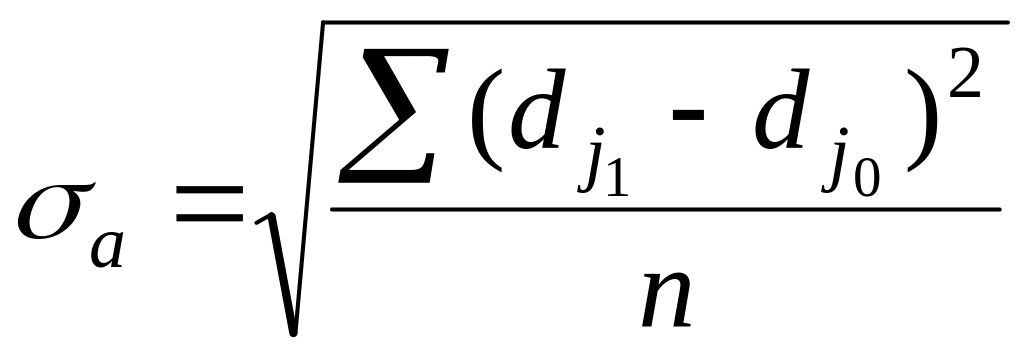
Квадратичний коефіцієнт розрахований на основі коефіцієнтів зростання чутливіше відповідає на зміни в структурі:

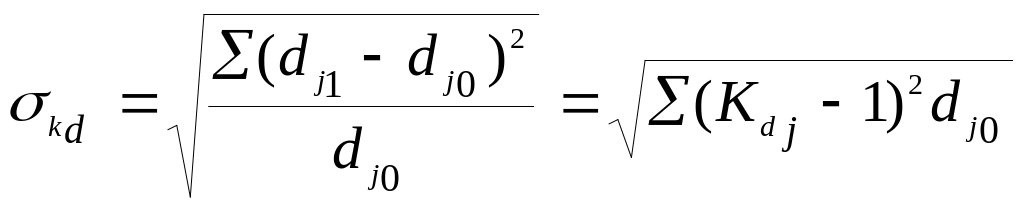
Результати розрахунків структури виробництва і характеристик структурних зрушень необхідно подати в табл.1.3.

Табл. 1.3.