
Shpory_TMM_Izm
.docx1)Основные понятия. Механизм – это система тел, предназначенная для преобразования движения одного или нескольких тел в требуемое движение других тел. Машина – это устройство, выполняющее механические движения для преобразования энергии, материалов или информации, с целью облегчения умственного и физического труда чел-ка.Различают группы машин: энергетические, технологические, транспортные, информационные, кибернетические, машина-автомат, автоматическая линия.Звено – это одно или несколько жестко соединенных тел, входящих в состав механизма.В каждом механизме имеется стойка (звено неподвижное или принимаемое за неподвижное).Звенья подразделяются на:неподвижные(стойка, неподв. направляющая) и подвижные(кривошип-звено, совершающее полный оборот вокруг неподвижной стойки; шатун-звено шарнирно связанное с другими звеньями мех-ма и совершающие сложные движения; коромысло-звено, совершающее колебательное движение вокруг стойки в пределах какого либо угла; ползун-звено, совершающее поступательные перемещения по неподвижной направляющей; кулисная пара-1.кулиса-звено, соверш. вращ. или колеб. движ. вокруг неподвиж. стойки 2.камень кулисы-звено, совершающее поступательное перемещение по подвижной направляющей; кулачок-звено, имеющее криволинейный профиль и полностью определяющее движение звена на выходе; зубч. колесо- это вращающее звено, имеющее нарезанные зубья, которые обеспечивают непрерывное движ. парных звеньев) |
2) Кинемат. пары. Классификация. Кинематическая пара – это подвижное соединение двух звеньев, допускающее вполне определенное относ. движение. Кинематические пары (КП) классифицируются по следующим признакам:1. по виду места контакта (места связи) поверхностей звеньев:• низшие, в которых контакт звеньев осуществляется по плоскости или поверхности ( пары скольжения );• высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием). 2. по относительному движению звеньев, образующих пару: • вращательные; • поступательные; • винтовые; • плоские; • сферические. 3. по способу замыкания (обеспечения контакта звеньев пары): • силовое (за счет действия сил веса или силы упругости пружины); • геометрическое (за счет конструкции рабочих поверхностей пары). 1. по числу условий связи, накладываемых на относительное движение звеньев ( число условий связи определяет класс кинематической пары ); 2. по числу подвижностей в относительном движении звеньев. |
1.Зубчатые мех-ы. Наиб. рапрост. в тех-е получ. зубч. мех-ы. Они отлич. простотой изготов-я и высок. точностью передачи зак. движ. от одного звена к др. Зубчатые передачи с пост. передат. отнош. 1.По виду зацепления: а)внешнее(напрал. ω1 и ω2 противоположны);б)внутреннее(ω1 и ω2 совпадают). 2.По взаимному расположению осей:а)цил. передачи с паралл. осями, котор. при лин. кас. активных прифилей имеют прямозубые, косозубые и шевронные колеса.б)конич. передачи с пресек. осями, котор могут иметь косозубые, прямозубые, кругозубые колеса. в) гиперболоидные передачи с перекрещивающ. передачами , к ним относят винтовые и гипоидные, червячные передачи. Еще бывают: 1 волновая зубч. передача; 2.пер.с цевочным зацеплением; 3.передача с реечным зацеплением |
||||||||||||
3) Кинематические цепи. Кинематические соединения. Кинематическая цепь – это система звеньев, связанных между собой кинематическими парами.Кинематические цепи могут быть: Простые и сложные. В простой кинематической цепи каждое из ее звеньев входит в состав одной или двух кинематических пар, а в сложной кинематической цепи имеются звенья, входящие в состав трех и более кинематических пар. Открытые и замкнутые. В открытой (незамкнутой) кинематической цепи имеются звенья, входящие в состав одной кинематической пары, а в замкнутой цепи каждое звено входит в состав 2-х и более кинематических пар. Плоские и пространственные. Если точки всех звеньев кинематической цепи двигаются в одной или параллельных плоскостях, то такая кинематическая цепь называется плоской, в противном случае кинематическая цепь — пространственная, так как точки её звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые.
|
4) Степень подвижности механизма n-число подвижных звеньев, значит, степень их подвижности Wn=6n. Число степеней свободы механизма: W=Wn-S. P5-кол-во одноподвижн. кин пар; Р4-двуподвижных; Р3-трехподвижных; Р2-четырехподвижных; Р5- пятиподвижных. W=6n-5Р5-4Р4-3Р3-2Р2-Р1 W=5n-4Р5-3Р4-2Р3-Р2-одна общая связь; W=4n-3Р5-2Р4-Р3-две; W=3n-2Р5-Р4-три; W=3n-2Рн-4Рв, Рн, Рв-число нисш. и высш. кин. пар. Начальным назыв. звено, котор. приписывается одна или несколько обобщенных координат мех-а.
Мех-м – кин. цепь с одним неподвижн. звеном. |
2.Основные элементы зубч. колес Диаметр нач. окр. d=Pt/π d=mz Pt-окруж. шаг, т.е. длина дуги по нач. окруж. м/у двумя соотв. профилями зубьев Модуль зацепления m=Pt/π Делит. окр.- окр, котор явл. базов. для опред. разм. зубьев. В основн. нач. и делит. окр. совпад. d=dϖ=mz Головка зуба – часть зуба лежащ выше делит окруж.(высота ha) Ножка зуба – чать, лежащ. внутри делит. окруж.(hf) Полн. выс. зуба – h=hf+ha Обычно hf=1.25m, ha=m, h=2.25m, для укорочен. зубьев: hf=m, ha=0.8m, h=1.8m Угловой
шаг зубьев-
центр. угол, опирающ. на дугу окруж d,
равную окружн. шагу Pt.( Окружн. шаг еще можно представить как сумму толщины зуба S и ширины впадины e Pt=S+e Различают: а) колеса с равноделенным шагом S-e=Pt/2 б) колеса, у которых S<e.При этом в завис-и от точности обработки зубьев S=(0.49+0.5)Pt e=(0.51-0.5)Pt Окруж-ь, проходящ по верш. зубьев, называют окр-ю вершин зубьев da, а по впадинам-окруж. впадин зубьев df. da=d+2ha df=d-2hf |
||||||||||||
5) Избыточные связи. Пассивные звенья. Пассивные звенья – звенья, не влияющие на движение механизма в целом и создающие избыточные связи. Избыточные связи - это связи число которых в механизме определяется разностью между суммарным числом связей, наложенных кинематическими парами, и суммой степеней подвижности всех звеньев, местных подвижностей и заданной подвижностью механизма в целом. Например, в механизмах грохотов, приводе колес электровоза, чтобы повысить жесткость системы используют механизм параллельных кривошипов 1, 3 и шатунов 2, 4. Подсчет степени свободы при n=4, Рн=6, Рв=0 свидетельствует о том, что W=0. Однако если EF=BC=AD и AE=DE, EB=FC, то наличие звена 4 не изменит кинематические свойства шарнирного четырехзвенника для которого W=1. Если из схемы удалить звено 4, то относительное движение др. звеньев останется неизменным, поэтому связь EF называется избыточной, а звено 4 пассивным. Рассмотрим кулачковый мех-м, состоящий из кулачка 1, ролика 2, ползуна 3 и стойки 0. В этом случае n=3, Рн=3, Рв=1 и W=2. Для исследования кинематики мех-а можно исключить ролик 2 как лишнее звено, приводящ. к избыточной подвижности, но не меняющее общую степень подвижности. |
6)Замена высших пар низшими. Заменяющий мех-м – мех-м, полученный в результате замены высших пар низшими. На рис. рассматривается способ получения заменяющего механизма на примере трехзвенного механизма с высшей парой, элементы которой представляют собой произвольные кривые аа и вв. W=3*2-2*2-1=1 Для построения заменяющего механизма в точке К проводится нормаль nn и отмечаются на ней центры О1 и О2 кривизны кривых аа и вв. Эти центры принимаются за шарниры, образующие вращательные пары, в которые входят условные звенья АО1 и О1О2, ВО1 и О1О2. Таким образом, заданный мех-м может быть заменен эквивалентным ему мех-м шарнирного четырехзвенника АО1О2В. Высшая пара в т.К заменяется условным звеном 3 (О1О2), т.е. шатуном. W=3*3-2*4-0=1.
В случ. когда один из соприкасающихся элементов будет представлять собой некотор. кривую аа, а второй – прямую вВ, центр кривизны профиля вВ будет в бесконечности, поэтому условное звено 3 со звеном 1 входит во вращательную пару в центре кривизны О1, лежащего на нормали nn, а со звеном 2 – поступательную пару в точке К.
Если одним из эл-в явл. прямая(звено 2), а другим-т.К, то замена высшей пары в т.К сводится постановке условного звена 3, в частности ползуна, входящего во вращательную пару в т.К, со звеном 1 и в поступательную пару со звеном 2. Таким образом, любой плоский мех-м с высшими парами может быть заменен мех-м, имеющим только низшие кин. пары. Для заменяющ. мех-а структурная формула: W=3n-2Рн. |
3. Передаточное отношение и передаточное число Передаточное отн. (U) – отношение угловой скорости ведущего элемента (ω1) механической передачи к угловой скорости ведомого элемента(ω2). По харак. передат. отнош зубч. передачи быв.:а) с пост. передат. отнош(с круглыми зубч. колесами) б) с переменным.( с не круглыми) Механизмы с передаточным отношением больше единицы — редукторы (понижающие редукторы), меньше единицы — мультипликаторы (повышающие редукторы). Передаточное
число(U)
рассчитывается как отношение числа
зубьев ведомой шестерни (z2)
к числу зубьев ведущей шестерни (z1)
|
||||||||||||
7.1) Согласно классификации мех-в по Ассуру-Артоболевскому самым простым мез-м явл. двухзвенный мех-м. Он состоит из двух звеньев: подвижного 1 и неподвижного 0(стойка). Группа Ассура – это кин. цепь, которая в случае ее присоединения свободными элементами к стойке получает нулевую степень подвижности. Wа=0 => 3n=2Рн Группу, состоящую из двух звеньев и трех возможных кин. пар назыв. двухповодковой гр. Если имеется двухпов. гр. с тремя вращ. парами А, В, С, где свободными поводками явл. звенья 2 и 3(рис.а), то при присоединении шарниров А и В к стойке(рис.б), получается нулевая степ. подвижности(W=0). Если эту же гр. соединить с начальным мех-м, то образуется шарнирн. четырехзвенник(рис.в), у которого W=1, то есть равна подвижности нач. мех-а.
Перв. модифик. – структ. группа, имеющ. только вращ. кин пары.(рис.а). Если одну из концевых пар заменить на поступательную, то получится вторая модификация(рис.г). Присоед. этой гр. к мех-у перв. класса дает кривошипно-ползунный мех-м.
|
7.2) Третья модифик. – поспутельной парой заменена средняя вращ. пара.(кулисные механизмы)
Четв. модифик. – две крайние вращ. пары заменены поступательн.(тангенсный мех-м)
Пятая модифик. – поступат. парами заменяются одна из крайних и средняя вращ. пары.(синусный)
Трехповодков. – гр., содержащ. четыре звена и шесть эл-в подвижн. соед. В этих гр. имеется базовое звено, а остальные явл. поводками.
Четырехповодков. – шесть звеньев и девяти кин. пар. Если к нач. мех-у присоединены одновременно несколько гр. Ассура, то класс мех-а в целом опред-я наивысшим классом группы. Класс мех-а зависит от выбора ведущего звена. пусть дан подш. |
4.Основная теорема зацепления(Виллиса) Если задано передат. отнош., то профили зубьев зубчатого зацепления следует проектировать так, чтобы общая нормаль к ним, проходящая ч\з т. К их касания, делила межосевое расстоян. О1О2=аω на отрезки О1Р и О2Р, отнош. котор. обратно пропорц. отнош. углов. скор-й.
P-полюс зацепления. Соприкасающ. профили раб. пов-й зубьев, построенные в соотвеств. с усл. Виллиса назыв. сопряж. профилями. Из основной теоремы следует, что сопряженные профили должны располагаться так, чтобы общ. нормаль в люб. точке контакта проходила ч\з полюс зацепления Р. |
||||||||||||
1.Трение скольжение в поступательной кин. паре. Пусть на ползун действует активн. сила Р. При этом масса ползуна m, его ск-ть V и ускорение а. Необходимо установить завис-ти м/у углами α и φ при которых ползун движ. ускоренно, равномерно или замедленно.
Чтобы отложить Q нужно повернуть N на φ по скор-ти. Ур-е движ. ползуна имеет вид: ma=P+Q(1). Система сил P и Q имеет равнодействующую: R=P+Q(2). Из 1 и 2 следует: R=ma(3). Равнодейст. можно вычислить использ.3 или 2, для реш-я котор. использ. граф. метод. Спроектируем ур-е 1 на оси коорд. X и Y. X: ma=Psinα-Fтр(4) Y:0=-Pcosα+N(5) Из 4 использ. 5 получ.: ma= Psinα-µN= Psinα-tgφN=N/(cosφ)sinα-tgφN=N(tgα- tgφ)(6). Из 6 следует:α>φ, то ускоренно; α=φ, то равномерно; α<φ, то замедленно. Пусть тело нах-ся в сост. покоя. к нему приложена некотор. активн. силу Р. если α<φ0, то тело останется в состоянии покоя; α>φ0, то тело начнет двигаться |
2. Трение во вращательной кин.паре. Часть вала, входящ. в подшипник назыв. цапфой. Пусть дан подш.скольжения. При этом к цапфе прилож. пара сил с мом-м М. представим данный мом. в виде произвед: M=Ph. При этом пусть цапфа вращ с ω=const. При вращ цапфы т.К где прилож. реакц. подшип. на цапфу смещается на встречу вращ. цапфы. P+Q=0(1). Т.к. цапфа в направл. OY не перемещ., то из 1 следует: Q=-P, т.е. Q II P. Ч/з т.К проводим лин. действующ. силы Q, которая будет являтся касат. к
окруж. рад.
Т.к.
углы тр. малы, то sinφ=tgφ,
отсюды следует: Круг рад. назыв. круном трения. Мом-т: Mтр=Q назыв. мом. тр.
Круг тр. позволяет опред. точку прилож. ревкц. подшипника на цапфу. Ур-е
вращ. цапфы вокруг своей оси:
Отсюда следует: h> , то цапфа вращ. ускоренно h= , то равномерно h< ,то замедленно |
5.Скорость скольжения профилей
N1K=N1P-KP N2K=N2P-KP
= Из подобных треуг. О1N1P1 и O2N2P следует, что PN2/PN1=O2P/O1P=ω1/ω2, т.е. ω2PN2=ω1PN1 Тогда
зацеплении.
|
||||||||||||
3.Трение в высшей кин.паре. Пусть на неподвижный цилиндр нагружен силой Р.Кривая распределения вызванных напряжений смятия будет симметричной, следовательно, линия действия равнодействующей N этих напряжений совпадает с линией действия силы Р. Под действием R начнется перетаскивание цилиндра, которое сопровождается наруш. симм. распределения напряж. смятия. Равнодейст. N сдвинется на плечо трения качения k
В т. К кроме силы N возник. Fтр. Услов. равновесия: X: R-F=0 или R=F(1) Mk: Pk-Rh=0 или R=rP/h(2) Поскольку т.К явл. мгнов. центром скор. а мгнов. относит. движ. цил. отсутст. то реакц опоры может сосотавлять с нормалью nn любой угол φn, но не более φ0. Тогда N=Qcosφn F=Qsinφn.(3) Подставляем 3 в 1 и 2 и учитываем N=P находим tgφn=k/h или fn=k/h. Отнош. k/h для большинства машиностроит. материалов значит. меньше коэфф. тр. скольжения в нач. движ. f0. Если лин. дейст. движ. силы R, приложенной к неподвижному катку, пересек. плечо тр. кач. k или касается его, то каток остается неподвижн. |
7.Длина зацепления, активный профиль, коэфф. перекрыт. и его физ. св-ва. Длина зацепления – участок В1В2, в т.В1 профили входят в зацепление, а в т.В2-выходят из него. Активный профиль-раб. участки профиля, где происходит взаимодействие пар зубьев. М\у окр-ю вершин зубьев одного колеса и окр-ю впадин другого имеется радиальн. зазор С=hf-ha Боков.
зазор
Основ. шаг Pb опред. отрезком К1К2 по лин. зацепл. LM м\у двумя точками К1 и К2. Pb=Ptcosα Коэф.
перекрытия
|
6.Построение эвольвентных профилей. Пусть прям. АВ касается основн. окруж-ив т.N. Требуется построить эвольвенту, описываемую т.К. Для этого разбиваем основную окружность возле точки N на дуги с хордами 20 мм. И проводим через полученные точки касательные к основной окружности, фиксируем на линии зацепления отрезок NK.. Ставим острие циркуля в точку N1 и проводим дугу K1K1 радиуса N1K1 до середины соседних областей с точкой К (приблизительно). Оставив карандаш в точке K1, перебросив острие в n2, изменив раствор циркуля, проводим дугу K1K2 до середины соседней области (приблизительно) радиусом n2K2. Оставив карандаш в точке K2, перебрасываем острие циркуля в точку n3 и проводим дугу K2K3 до середины соседней области радиусом n3K3 и т.д. Аналогично строится участок КК0. Полученная крив. состоит из дуг кругов, однако она практически не отличается от эвольвенты. Геометрическое место центров кривизны какой либо плоской кривой назыв. эволютой, а сама кривая по отнош. к эволюте - разверткой или эвольвентой. |
||||||||||||
8.Определение Zmin приобработке методом копирования Диаметр нач. окруж. малого колеса d1 принимается произвольно, а диаметр большего опред. ч\з заданное передат. число U1\2: d2=U1\2d1 Строят нач. окруж. диаметрами d1 и d2 и ч\з т.Р их касания проводят прямую LM(лин.зацепления), составляющую угол зацепления α с перпендикуляром РЕ к межосевой линии О1О2. Затем из центра О1 на LM опускают перпендик. О1N1, а из центра О2 проводят окруж. рад. О2N1. Эта окруж. явл. окр. вершин зубьев большего колеса, а число зубьев: Zmin=d1/m’, где m’-временн. модуль зацеплен., зависящий от высоты головки зуба ha величина которого опред.из выполненного чертежа, с точностью до десятых долей.
|
9. Определение Zmin приобработке методом огибания(долбяк) Снач. приизвестн. модуле зацепления m и числе зубьев долбяка Zд опред. диаметры нач. и окружн. вершин зубьев: dд=mZд dад=dд+2hад где высота зубьев долб. hад приним. равной высоте ножки зубьев hf оюъбрабатыв. колеса. Затем чертят эти окружн. и ч\з выбран. на окружн. диаметр dд из полюса зацепления Р проводят прямую LM под углом α к линии РЕ_|_ Род. Далее в т. N1 пересеч. окруж.вершин зубьев долбяка с линией LM восстанавливают прпендик. О1N1 до пересеч. с продолжен. прям. ОдР. Получ. т.О явл. центром малого обрабатываемого колеса, а О1Р-радиусом его нач. окруж. Тогда Zmin=2O1P/m. |
10. Определение Zmin приобработке методом огибания(гребенка) проводят три прям.(нач., прям. вершин и прям. впадин зубьев гребенки) и чертят ее режущий профиль. при этом hагр=hfгр=hf. На нач. прям. выбир. произвольн. т. Ри ч\з нее проводят прям, перпендик. к этим прямым, а также линию LM под углом α к нач. прямой. Затем из т.N1 пересеч. прямой вершин зубьев гребенки с линией LM восстанавливают перпендик. О1N1 до пересеч. с горизонт. линией. В результ. т. О явл центром, а О1Р-радиусом нач. окруж-и обраб. колеса. Наим. число: Zmin=2O1P/m. Получ. дробн. число Zmin округляют в больш. стор. до целого знач. и опред. число зубьев Z1 меньшего колеса. Число зубьев больш. колеса Z2 вычисл. ч\з передат. отнош. Z2=U1\2Z1 и округ до ближ. целого числа. |
||||||||||||
11.Определение сил мом-в, мощности и КПД в прост. редукторе. Прост. редуктор: например, состоящ. из паров. турбины Т, генерат. эл. тока Г и редуктора скор-и Р. Ведущ. вал 1 редуктора связан муфтой с валом ротора турбины, а ведомый вал 2 – с валом ротора генератора. Активн. мом.(М1) – момент пары сил, возник. на валу 1 ред. Мом. полезн. сопротивл(Мт).- мом. численно равный активн. мом-у, но противоположн. по направ. Пусть известны эффект. мощ-ть турбины Nэф(кВт), частота врыщ. ротора турб. n1(об\мин) и передат. отнош. ред. U1\2/ Требуется опред. активн. мом-т Мг, прилож. к валу ротора мощ-ть Nг, потребляемую генератором. Активн. мом-т, прилож. к валу 1 ред.: М1=1000(Nэф\ω1), где ω1=(πn1)/30 КПД: η=Аплз/Азтр. Если брать раб. за одну сек., то: Аплз=Мгω2 Азтр=М1ω1 η = Мгω2/ М1ω1 Учитывая, что Мг = -М2, а ω1/ω2=U1/2 получится: η= - М2/(М1U1/2) в случ. внешн. зацеплен: η=0.95-0.98 внутр: 0.96-0.99 Таким образом мом. редук. М2 вычисляется М2=-М1U1/2η, а мощн. ген: Nг=Nэффη |
12. Передат. число, КПД, и мом-ы многоступ. редукт. Многозв. зубч. мех-м можно рассматривать состоящим из нескольких трехзвенных зубч. мех-в, кажд. из котор. назыв ступенью. Рассм. двухступ. редуктор. Общ. передат. отнош. мех-а составляет U1/3=ω1/ω3 или U1/3=ω1/ω2ω2/ω3 и приняв во внимание: ω1/ω2=U1/2 ω2/ω3=U2/3 получится: U1/3=U1/2U2/3 т.е. передат. отнош двузступ. ред. равно произведению передат. отнош.отдельн. его ступ. Для данн. примера передат. число отдельн. ступ. составляет: U1/2= - Z2/Z1 U2/3= - Z3/Z’2 а для двухступ. ред.: U1/3=U1/2U2/3=(Z2Z3)/(Z1Z’2) Если ред. имеет К ступ.,то U1/k+1=ω1/ωk+1=(Z2Z3…Zn) Для опред. связей м/у мом. двухступ. ред-в разбивают на две отдельн. ступени I и II, представ. собой два прост. ред. В этих ред-х М1 и М’2 будут активн., а мом-ы М2 и М3- полезн. сопротивл. Тогда: M2= - M1U1/2η1/2 и M3= - M’2U2/3η2/3 приняв во внимание, что M3=-M1U1/3η1/2η2/3 (1) Коэфф. полезн. действ. всего редуктора будет равен: η1/3= - (М3ω3)/(М1ω1)= - М3/(М1U1/3) (2) Подставив выраж. 1 в 2 получим: η1/3=η1/2η2/3 Таким образом, КПД двухступ. ред. равен произвед КПД его ступ. Тогда мом-т на выходн валу: М3= - M1U1/3η1/3 а для ред., имеющ К ступ.:
|
13. Планетарн. ред-р, устр-во и классификац. Планетарный редуктор (дифференциальный редуктор) — один из классов механических редукторов. Редуктор называется планетарным из-запланетарной передачи, находящейся в редукторе, передающей и преобразующей крутящий момент. Планетарный редуктор может быть с одной или более планетарными передачами, Достоинства: высокий КПД; компактность планетарн. узло; соосность выходн. и входн. вала. Зубч. колесо 1, вращающееся вокруг неподвижн. оси назыв. солнечным, а колесо 2 с вращающейся осью, котор. обкатывает центр. колесо – планетарным, или сателлитом. Подвижн. звено 3, на котор. располаг. оси сателлитов назыв. водилом, а неподвижн. центр. колесо 4(зубчатый венец) – опорным. Как правило, планет. мех-ы изготавливаются соосными, т.е. оси входного и выходного звеньев совпад. Они облад. одной степ. свободы и обязательно имеют опорное колесо. На прак. часто встреч. мех-ы, не имеющ опорн. звена, у которых число своб больше единицы(W>1). Такие мех-ы назыв. дифференциальными. |
||||||||||||
14.Опред. передат отнош и КПД планетарн. ред-ра 1.Планет. ред. превращ. в непланет. закреплением водила. При этом всем звеньям сообщ. углов. ск-ть, равн. по велич. и противоположн. по направ. углов ск-ти водила ω3. Тогда водило 3 станов. неподвижн., а опорное звено 4 – подвижн.=>редуктор превращ. в двухступенчатый., состоящ. из последов. соед. пар зубчат. колес 1,2 и 2,4. 2.Составл. табл.углов. скор-й звеньев для обоиз мех-в.
углов.ск-ть ω2 звена не входит в табл., т.к. колесо 2 явл. промеж., а общ. передат. отнош. U1/3=ω1/ω3 не зависит от углов. скор. промеж. зубч. колес. 3.Опред.
передат. отнош. Внач. рассматрив.
непланет. мех-м, для которого
а
следовательно,
mZ4=mZ1+2mZ2
или Z4=Z1+2Z2,
тогда
4.Опред.направл. углов. скор. и моментов. Для нашего редукт. момент М1явл. активным, а М3 – моментом полезного сопротивления. Направл. углов. скор. зависят от знака, т.е. если U1/3>0, то в планет. редукторе направления ω1 и ω3 совпадают, если U1/3<0, то направл. ω1 и ω3 противоположны. Направл. углов. скор-и (ω1 -ω3), с котор. вращ. вал 1 непланет. редуктора, зависит от числен. знач ω1 и ω3. Если ω1 >ω3, то оно останется без изменения по отнош. к направл. вала 1 планет. редуктора, а если ω1 < ω3, то это направл. будет противоположн. 5. Выявляется ведущ. звено в непланет. мех-е. по направл. угловой скор-и и момента. Связь
м/у моментами в ступ. редукторе согласно
котор.: В
рассматр.
примере при ω1 >ω3 направл. мом-а М1 и
углов. скор.( ω1 - ω3) совпад. следовательно,
звено 1 явл. ведущ(вщ), а ведомым(вм)
будет звено 4. Тогда:
6.
Опред. знач.
мом-в:
7. Вычисляется КПД планет. редукт.
для
исследуемого редуктора примет вид:
после
подстановки 1 в последн. выраж получ.:
|
1.Исследование и классиф. кулачков. мех-в простейш. км состоит из трех звеньев: кулачка 1, котор. явл. ведущ. звеном, образующ со стойкой О низш. кин. пару, толкателя 2 – ведомого звеа, образующ. с кулачком высш., а со стойкой низш. пару. 1)По виду движ. кулачка: вращающ.; качающимися(φ=φ(t);; паступательно движ (S=S(t))..
2)по виду движ. толкателя: мех-ы, толкатели котор. соверш. колебат. движ(φ=φ(t); мех-ы, толкат. котор. соверш. возвратно-поступат. движ. (S=S(t)); толкат соверш. сложн. движ.
3)по проф. раб. пов-и толкат: остроконечные; роликовые; тарельчатые; сферические
Распространенные преобразован. движ.:
|
2. Кин. анализ КМ. Определен. скор-и и ускор. толкат. Кин. исследов. мех-в включ. в себя: 1)построен. плана мех-а и диаграммы полож. толкат., при этом заданы разм. км, профиль кулачка и конструкц. толкателя. 2)определен. скор-й и ускор-й выходного звена, а также сил действующ. на толкатель. а) Кулачк. мех-м с роликом и коромыслом. АВ=r1+r2,
поэтому не наруш. движ. звеньев км-а,
к нему можно присоед. дополнит.
звено(шатун), связав его шарнирами А
и В с кулачком и коромыслом. Из этого
следует, что траектор. движ. т В кулачк.
мех-а не отлич. от траектор. движ. т.В
замен. мех-а ОАВС, а ее скор-ть и ускор-е
б) с тарельч. толкателем Заменяем
на кулисн. мех-м с поступат. движ.
кулисой, в котор ускор. и скор.:
в) с поступат. движ. кулачком АВ=r1+r2, поэтому не измен. движ.звеньев кулач. мех-а к нему можно присоед. дополнит. звено АВ(шатун), связав его шарниром В и А с кулачком и коромыслом соответственно, а кулачок заменить ползуном. При этом движ. т А кулачк. мех-а не будет отличаться от движ. т. А мех-а с ползуном и коромыслом.
|
||||||||||||
6. Силов. анализ КМ с тарельч. толкат. В
этом случ. давлен. кулачка δ принимают
равн. углу тр. φ. Т.е.происходит тр.
скольжение.поскольку в КМ исследоа.
кинематики ведется методом обращ.
движ., сила давлен QB
кулачка на
толкат. отклон от нормали на угол φ
против перемещ. толкат. относит.
кулачка. Значит направл. силы QB
зависит от
направл. вращ. кулачка. Расчет сил
|
||||||||||||||
7. Силов. анализ КМ с коромыслов. толкат. В
Мех-е, где кулачок приводит в движение
коромысло, треб. опред. силу давлен.
кулачка на ролик
Равнодейств.
R=mas
, прилож. к
коромыслу отстает от центра масс на
расст.: H=M/R=(Jε)/R
и направл. по ускорен. as.
В этом случ:
|
||||||||||||||
5.Силов. анализ КМ с роликов.. толкат. Можно считать, что ролик жестко связан с толкат., тогда: R=maB Равнодейст: Составл.
ур-я мом относит C’и
D’:
а
силы Q
и R
на чертеже пропорц. отрезкам cd
и od:
cd=Q/K
(7) od=R/K
Следоват. многоугольн. oabcd
представ. собой план сил, выполненный
в масштабе K=(Q-R)/oc
и K=(Q+R)/oc,
если R
направл. в противоположн. стор. Из
соотнош. 6 следует, что при cos неогранич.
возраст. Такая же картина наблюд.,
когда т. О и С совпад. и согласно выраж.
7 K= Подобн.
явл. возможно: 1) По углу давлен.
.
При
2)
по кэфф. тр. скольж. f
или углу тр. φ/. Если
3) по геометрич. размерам x и l. При увелич. x / l до x/l=(1-ftgδ)/(2ftgδ), самотормож., поэтому x/l<(1-ftgδ)/(2ftgδ)
|
||||||||||||||
1.Достоинства и недостатки ДРМ ДРМ по классиф. А.-А. – мех-ы перв. класса: 1 – вращ.звено(ротор) и 2-неподвижн(статор). Достоинства:1)позволяют реализовать больш. мощности в довольно компактн. установках; 2)простота конструкц; 3) надежность. Пр:вентилятор, центробежн. насосы, компрессора. |
||||||||||||||
2.Определение статич. и динамич. давлен. цапфы на подшипник. Пусть
ротор массой m
вращ. в подшипниках А и В с пост. углов.
ск-ю ω. главн. центр. ось инерц. паралл.
оси вращ. ротора и отстоит от нее на
расстоянии
Сист.
сходящ. сил {P1,P2,Q1} R
- вращ.
|
||||||||||||||
4.Три режима движ. цапфы в подшипнике
а)
б)
в)
|
5.Уравновешивание ротора при конструировании мех-а. Рот. счит. неуравновешенню, если главн. центрю ось инерц. не совпад. с осью его вращ.
1 и 2- усл. отсутст. дин. давл. Для уравновешиван. люб. рот. необходимо установить два противовеса. Плоскости коррекции – плок. в еотор. устанавл. противовесы.
|
6.Статическая балансировка и ее недостатки Мтр=kQ
Недостаток: низк. точ-ть уравновешиван. |
||||||||||||
7.Динамич. балансировка роторов. Станок
Шитикова: маятн. рама 1, опираясь на
пруж. 2, может колеб. относит. гориз.
оси, проходящ. ч/з т.О. Балансир. ротор
3 устанавлив. на опорах 4, жестко связан.
с маятников. рамой. Принцим работы
основан на явлении резонанса. Снач.
задают расст.
|
8.Допустимая неуравновешенность
|
1.Назначение и уст-во КПМ. КПМ относят к II классу шарнирно-рычажн. мез-в. В двиг. внутр. сгоран. их применяют для преобразов. возвратно-поступат. движ. ведущ. ползуна(поршня) во вращ. движ. ведомого кривошипа(коленч. вала); в компрессорах для преобраз.вращ. движ.ведущ. звена кривошипа в возвратно-поступат. движ. ведомого звена – ползуна. КПМ состоит из ползуна 1, совершающ возвратно-поступат. движ., шатуна 2, выполняющ. плоско-паралл. движ., кривошипа 3, совершающ. вращ. движ., стойки О. На валу кривошипа жестко закрепл. маховик, чтобы вращ. звено 3 имело опред. мом-т инерции относит. оси вращ. |
||||||||||||
2.Аналитич. метод. опред. скор-и и ускор-я |
3.Индикаторная диаграмма и силы прилож. к ползуну Индикаторн.
диаграмма
На участ. 1-2 присх. сжатие горюч. смеси, 2-3 – горение смеси, 3-4 – расширен. газов, 4-5 выпуск. отработанных газов, 5-1 – продувка цил-а, где давл. падает до атмосферн. давл. Ратм. Сила
горюч. смеси, действ. на поршень:
Для построен Р=Р(SB) необх. знать Р:
P=R+Q, где R сообщ. ускор. потупат.- движ. массами
Если выразить все силы а одном масш. Кр, то
|
4.Мом-ы, действующ. на кривошип. |
||||||||||||
5.Степень неравномерности колеб. кривошипа в КПМ. Степень
неравномерности
– характеризует размах колеб. углов.
скор-и по отнош. к ее средн. знач. : |
6.Опред.мом-а инерц. моховика. Для
опред. мом-а инерц. J
моховика рассматр. движ. кривошипа
м/у двумя соседн. экстремумами его
углов. скор., например, в пред.
Принимая
соотнош.:
Aизб= Опред.
мом. инерц. моховика JM
производится
по заданн. усл. движ.(т.е. по задан.
велич.
),
в проц. проект. машины и для практ.
расчетов принимается:
|
7.Назнач. моховика и его регулир. возд. Все
звенья мех-а обладают инерт-ю. Как
известно из физики, чем инертнее матер.
тело, тем медленнее происходит измен.
его скор-и, вызыв. действием прилож.сил,
поэтому, чтобы получ. вращ. звена(вала)
машины с неравномерностью, не превышающ.
треб. велич., инертность этого звена
со всеми жестко связанными с ним
деталями надо сделать достат. большой.
Для этого на валу маш. необходимо
закрепить добавочн. массу, выполнен.
в виде махового колеса и назыв.
маховиком.
Итак, основн.
назнач. маховика сост. в выравнивании
колеб угл. скор-и и удержан. их в
пределах, устанавливаемых велич.
коэфф. неравномерности δ. Регулирующ.
воздейст.: в пределах углов
и
|
||||||||||||
|
|
|

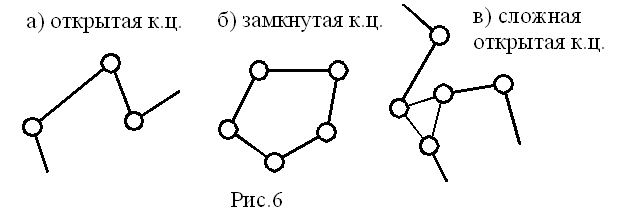
 =2π/z)
=2π/z) n-число
оборотов в мин; d-диаметр
нач. окр..
n-число
оборотов в мин; d-диаметр
нач. окр..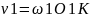
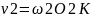

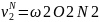
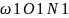 =
=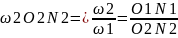
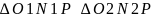

 ,
тогда из построения следует
,
тогда из построения следует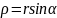 ,
r-рад.
цапфы.
,
r-рад.
цапфы.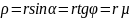
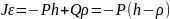 .
.

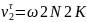


 -ск-ть
скольж. при внешн.
-ск-ть
скольж. при внешн.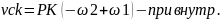
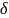 -
разность вершины впадины е
и толщины зуба
S
-
разность вершины впадины е
и толщины зуба
S )
– отношение длины зацепления B1B2
к основн. шагу Pb.
Он показывает
сколько пар зубьев в среднем находится
в зацеплении одноврем.
На практике допустимое знач., котор.
обеспечив. непрерывность процесса
зацепления, принимают не менее 1,05,
т.е. с 5%-м запасом. В норм. эволь. колесах
)
– отношение длины зацепления B1B2
к основн. шагу Pb.
Он показывает
сколько пар зубьев в среднем находится
в зацеплении одноврем.
На практике допустимое знач., котор.
обеспечив. непрерывность процесса
зацепления, принимают не менее 1,05,
т.е. с 5%-м запасом. В норм. эволь. колесах
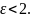
 /(Z1Z’2…Zn-1)
/(Z1Z’2…Zn-1) . Кроме того, для
кажд. прост. ред I
и II
можно записать: М1+М2+М’4=0
M2+M3+M’’4=0,
где M’4
и M’’4
– внешн.
мом-ы, прилож. к корпусам эттих ред-в,
а их сумма M’4+M’’4=M4
представ.
собой мом-т, прилож. к корпусу ступ.
ред. Если сложить два предпослед.
выраж, то М1+М2+М4=0.
. Кроме того, для
кажд. прост. ред I
и II
можно записать: М1+М2+М’4=0
M2+M3+M’’4=0,
где M’4
и M’’4
– внешн.
мом-ы, прилож. к корпусам эттих ред-в,
а их сумма M’4+M’’4=M4
представ.
собой мом-т, прилож. к корпусу ступ.
ред. Если сложить два предпослед.
выраж, то М1+М2+М4=0.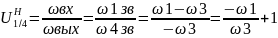 приняв во внимание, что
приняв во внимание, что
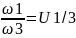 – передат.
отнош. планет. мех-а, получ.:
– передат.
отнош. планет. мех-а, получ.:
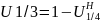 .
Если выразить
.
Если выразить
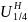 .
ч/з числа зубьев колес, то
.
ч/з числа зубьев колес, то
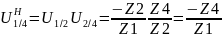
 .
Неизв. числа зубьев опред. из усл.
соосности мез-а с учетом геометрии
его строения: d4=d1+2d2,
где d1,
d2, d4 –
диаметры нач. окруж. соответств. колес.
.
Неизв. числа зубьев опред. из усл.
соосности мез-а с учетом геометрии
его строения: d4=d1+2d2,
где d1,
d2, d4 –
диаметры нач. окруж. соответств. колес.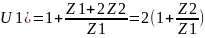
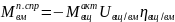
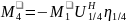 /
/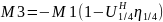 (1)
(1)


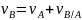
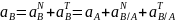

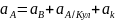 ,
где ak=0
– ускор. Кориолиса.
,
где ak=0
– ускор. Кориолиса.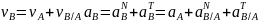
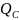
 производят по формулам 5 и 6 при φ=δ
На рис б. представл. грай. реш. ур-я 1
для данн. схемы. Следует учесть
производят по формулам 5 и 6 при φ=δ
На рис б. представл. грай. реш. ур-я 1
для данн. схемы. Следует учесть

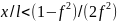
 станины
на коромысло. При этом известны: полож.
центра масс S,
масса m,
момент инерции J
и угловое ускор. ε коромысла, также
сила
станины
на коромысло. При этом известны: полож.
центра масс S,
масса m,
момент инерции J
и угловое ускор. ε коромысла, также
сила
 , прижимающ. коромысло к кулачку.
, прижимающ. коромысло к кулачку.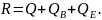 При анализе ур-я можно отметить, что
линия действ. силы
При анализе ур-я можно отметить, что
линия действ. силы
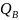 совпад.
с общ. нормалью кулачка и ролика, а
сила
совпад.
с общ. нормалью кулачка и ролика, а
сила
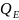 неизвестна ни по велич., ни по направл.
Воспольз. теор. Вариньона о моменте
равнодейств. относит т .Е и найдем силу
неизвестна ни по велич., ни по направл.
Воспольз. теор. Вариньона о моменте
равнодейств. относит т .Е и найдем силу
 :
RcE=
dE-
bE.
Откуда
:
RcE=
dE-
bE.
Откуда
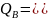 dE-
RcE)/(
bE).
Решен. уравнен. котор. показано на
рис.б позволяет опред. силу
и по велич., и по направл. Из последн.
выраж. следует, что самооторжен.
наступит при bE=0,
а это возможн, если линия действ. силы
проходит ч/з т.Е.
dE-
RcE)/(
bE).
Решен. уравнен. котор. показано на
рис.б позволяет опред. силу
и по велич., и по направл. Из последн.
выраж. следует, что самооторжен.
наступит при bE=0,
а это возможн, если линия действ. силы
проходит ч/з т.Е.

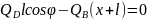 (3), где
(3), где
 .
В качестве третьего уравн. принимаем
урвн. 1 спроектиров. по направл. aB:
.
В качестве третьего уравн. принимаем
урвн. 1 спроектиров. по направл. aB:
 .
Из ур-й 2 и з следует:
.
Из ур-й 2 и з следует:
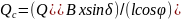
 .
После подстан. последн. соотнош. в 4
получим:
.
После подстан. последн. соотнош. в 4
получим:
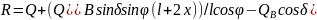 решен. котор. приводит к опред.
:
решен. котор. приводит к опред.
:
 ,
где f=tgφ
– коэфф. тр. скольжен. Из выражен. 2 и
3 следует:
,
где f=tgφ
– коэфф. тр. скольжен. Из выражен. 2 и
3 следует:
 =
= .
Если за масштабн. коэфф. принять
К(н/мм), то
.
Если за масштабн. коэфф. принять
К(н/мм), то
 ;
;
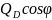 →a’b’
′=
→a’b’
′=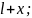
 --> oa,
ab,
bc.
Иском. велич. находят из соотнош:
=
Kdc;
--> oa,
ab,
bc.
Иском. велич. находят из соотнош:
=
Kdc;
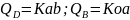
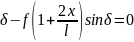 реакц.
реакц.
 следоват.
следоват.
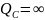
 .
Это указыв. на невозм.движ. толкат.,
т.е. возникнет самоторможение мех-а.
.
Это указыв. на невозм.движ. толкат.,
т.е. возникнет самоторможение мех-а.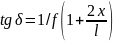 кулачк. мез-м
не раб., поэтому при конструирован.
необход. добиваться чтобы
кулачк. мез-м
не раб., поэтому при конструирован.
необход. добиваться чтобы

 ,
то самотормож. ., поэтому при конструирован.
необход. добиваться чтобы
,
то самотормож. ., поэтому при конструирован.
необход. добиваться чтобы
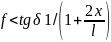 ,
, .
Пусть прилож.
силы Р1 и Р2, пост. по велич. и направл.,
пара сил с моментом М. Треб. опред.
давлен. подшипников на ротор.
.
Пусть прилож.
силы Р1 и Р2, пост. по велич. и направл.,
пара сил с моментом М. Треб. опред.
давлен. подшипников на ротор.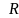 ;
;
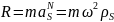 ;
;
 ;
;
 .
Задаем план сил:
.
Задаем план сил: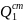 -
остается на месте
-
остается на месте


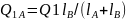

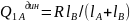
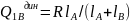


 и
и
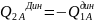 или
или
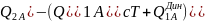
 и
и
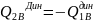 или
или
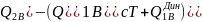


 подшипн.
изнашив. с одной стор., а цапфа с др. но
не равномерно
подшипн.
изнашив. с одной стор., а цапфа с др. но
не равномерно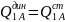
 начинает бить
подшипник (ударн. реж. раб. цапфы)
начинает бить
подшипник (ударн. реж. раб. цапфы) изм. от
изм. от
 до
подшипник
изнашив. неравномерно, а цапфа с одной
стор., происходит вырывание металла.
до
подшипник
изнашив. неравномерно, а цапфа с одной
стор., происходит вырывание металла.



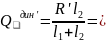
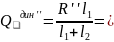
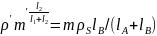 (1)
(1)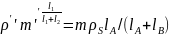 (2)
(2) ,
Jy,
Jz
- мом-ы инерц относит Z
и Y.
Динамич. силы давлен подш. на ротор
опред.:
,
Jy,
Jz
- мом-ы инерц относит Z
и Y.
Динамич. силы давлен подш. на ротор
опред.:
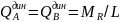
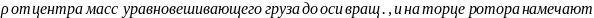
 они делили окружн.
рад.
они делили окружн.
рад.
 Затем берут кусок пластил., и поочередно
прикрепляют в указ. точкх. Сообщ. вращ.
ротору, замеряют амплитуды. Сопоставл.
получ. данн. нах. сектор в нименьш.
амплитудой, котор. дополнит делят на
неск. точек и повтор. процедуру. таким
образом находят полож. противовеса.
На втор этапе ротор устанавл. так,
чтобы плоскость уравновеш e”
не проходила ч/з ось вращ. маятников.
рамы, и по той же методике подпирается
урановеш. масса груза и его полож. в
пло-и e”.
Произвед. массы противовеса на расст.
центра масс до оси вращ. рназыв.
дисбалансом: D=m
.
При относит
небольш. дисбалансах знач. D
прямо пропорц. амплит. Z.
Тогда то. уравновеш. выраж. в виде
остаточн.
дисбаланса:
Затем берут кусок пластил., и поочередно
прикрепляют в указ. точкх. Сообщ. вращ.
ротору, замеряют амплитуды. Сопоставл.
получ. данн. нах. сектор в нименьш.
амплитудой, котор. дополнит делят на
неск. точек и повтор. процедуру. таким
образом находят полож. противовеса.
На втор этапе ротор устанавл. так,
чтобы плоскость уравновеш e”
не проходила ч/з ось вращ. маятников.
рамы, и по той же методике подпирается
урановеш. масса груза и его полож. в
пло-и e”.
Произвед. массы противовеса на расст.
центра масс до оси вращ. рназыв.
дисбалансом: D=m
.
При относит
небольш. дисбалансах знач. D
прямо пропорц. амплит. Z.
Тогда то. уравновеш. выраж. в виде
остаточн.
дисбаланса:
 ,
где
,
где
 -масса
пробн. груза;
-масса
пробн. груза;
 -расст.
от оси вращ. до центра массы пробн.
груза;
-расст.
от оси вращ. до центра массы пробн.
груза;
 -остаточн.
амп. после балансировки;
-остаточн.
амп. после балансировки;
 -первонач.
апмлит. колеб. рамы до балансировки.
Остаточн. дисбал. опред. отдельно для
кажд. плос-и и сравнивают их с допустимыми
знач. Должно выполняться усл:
-первонач.
апмлит. колеб. рамы до балансировки.
Остаточн. дисбал. опред. отдельно для
кажд. плос-и и сравнивают их с допустимыми
знач. Должно выполняться усл:
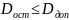



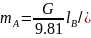



 =
= ,
т.к.
,
т.к.
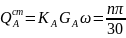 ,
то
,
то




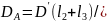 )+
)+ )
)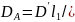 )+
)+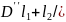 )
) – это граф. давл. внутри цил. в зав-и
от полож. ползуна.
– это граф. давл. внутри цил. в зав-и
от полож. ползуна.
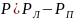
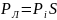





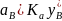
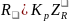

 Велич.
Велич.
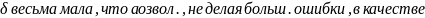 значения углов. скор-и
значения углов. скор-и
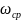 принять
принять
 Чем меньше
коэфф. неравномерности, тем меньше
размах колеб., тем равномернее вращ.
кривошип. Для кажд. вида машин имеется
своя допустимая величина. Обычно маш.
и мех-ы раб. в установившемся режиме,
котор. достиг. уменьш. степ. неравномерности
δ. Однако добиться условия, при котор.
δ=0 практически не удается из-за
необход-и безгранич. увелич. мом-а
инерц. J
вращ.
звена(моховика)
Чем меньше
коэфф. неравномерности, тем меньше
размах колеб., тем равномернее вращ.
кривошип. Для кажд. вида машин имеется
своя допустимая величина. Обычно маш.
и мех-ы раб. в установившемся режиме,
котор. достиг. уменьш. степ. неравномерности
δ. Однако добиться условия, при котор.
δ=0 практически не удается из-за
необход-и безгранич. увелич. мом-а
инерц. J
вращ.
звена(моховика) .
.
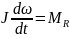
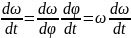
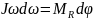 Проинтегрир. послед. выраж.:
Проинтегрир. послед. выраж.:
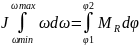 (2)
(2) из 2 следует,
что J=1/(
из 2 следует,
что J=1/(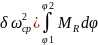 (3)
(3)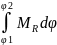 тогда
J=Аизб/(
тогда
J=Аизб/(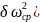 Если в 3
подставить
Если в 3
подставить
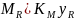 ,
,
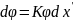 и вместо
и вместо
 и
и принять соотв. знач. оси абсцисс
принять соотв. знач. оси абсцисс
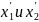 ,
то
,
то
 ,
где
,
где
 - избыт. площадь.
- избыт. площадь.
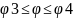 ,
где мом-т MR>0
и кривошип вращ. ускоренно, происходит
аккумулирование кин. энерг., а в пределах
,
где мом-т MR>0
и кривошип вращ. ускоренно, происходит
аккумулирование кин. энерг., а в пределах
 ,
где MR<0
и кривошип вращ. замедленно, идет ее
передача вращающемуся звену.
,
где MR<0
и кривошип вращ. замедленно, идет ее
передача вращающемуся звену.