5. Задание: интервальное оценивание параметров.

Построение доверительных интервалов для каждого из параметров уровней значимости 0,05 и 0,01.

• Указания к пункту 5.

Интервальное оценивание – это оценивание, при котором указывается интервал, накрывающий параметр с заданной наперед вероятностью.

Доверительным интервалом уровня значимости α для параметра называется интервал , для которого выполняется условие:

• Доверительный интервал параметра

Для построения доверительного интервала необходимо взять статистику, которая бы зависела от параметра , а её распределение от зависело бы.

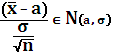– мы не можем использовать эту статистику, т.к. не известно, поэтому мы выберем статистику

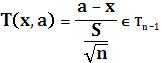– распределение Стьюдента с степенью свободы.

Получаем доверительный интервал для a:

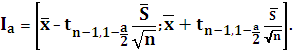
• Доверительный интервал параметра σ

Для построения доверительного интервала необходимо взять статистику: , где - распределение Пирсона с степенью свободы.

Доверительный интервал для параметра с уровнем значимости α:

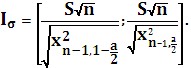
Значения квантилей берутся из соответствующих таблиц.

6. Задание: проверка гипотез:

• проверка гипотезы о виде распределения,

• проверка гипотез о каждом из параметров.

• Указания к пункту 6.

Статистической гипотезой называется утверждение о виде распределения генеральной совокупности. Проверяемая гипотеза называется нулевой и обозначается H₀. Наряду с ней рассматривают альтернативную гипотезу H₁.

• Проверка гипотезы о виде распределения

Гипотезы:

Для проверки гипотезы используем критерий согласия Пирсона:

Критерий применяется к группированной выборке.

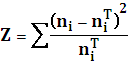, где n^T_i=nP_i.

Вероятность находится с помощью функции распределения

Таблица 3.

	Критерий согласия Пирсона (вид таблицы)
	№ инт Граница интервала F( ) 1 2 3 4 5 6 7 8
	– эмпирическое значение статистики критерия согласия Пирсона. 11,07 – критическое значение критерия Пирсона, полученное для доверительной вероятности 1-α = 0,95 при уровне значимости 5% и числа степеней свободы v=k-r-1=8-3=5.
	Замечание. При работе в Excel не требуется высчитывать вспомогательную переменную t, можно сразу находить Вывод: анализ результатов проверки статистических гипотез позволяет сделать вывод о том, что гипотеза о нормальном распределении не отвергается при уровне значимости α=0,05 т.к. значение не попало в критическую область . Или: анализ результатов проверки статистических гипотез позволяет сделать вывод о том, что гипотеза о нормальном распределении е отвергается при уровне значимости α=0,05 т.к. значение попало в критическую область.

• Проверка гипотез о каждом из параметров

1.Гипотеза о среднем , параметр известен, а параметр не известен.

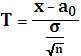, если справедлива , то

Тогда, если u_0,025 <T< u_0,975, то H₀ не отвергается с уровнем значимости 0,05. При α=0,05 u_0,975=1,96, u_0,025=-1,96

2. Гипотеза о дисперсии:

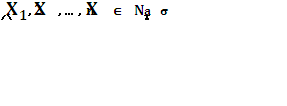, то есть параметр не известен.

при справедливой гипотезе H₀:

При α=0,05, если Z_0,025 <Z< Z_0,975, то H₀ не отвергается с уровнем значимости 0,05.