Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«Сибирский федеральный университет

Т. В. Крупкина

Методические указания

к выполнению расчетной работы

по курсу ТВиМС

по теме:

"Статистическая обработка выборки"

СФУ 2011

1. Задание: Получение выборки объема n предположительно нормально распределенной случайной величины.

Возможные методы получения: путем проведения эксперимента, наблюдения, измерения, получения статистических данных INTERNET или моделирования.

Число случайных чисел: n = 100 + двузначное число в конце номера зачетки.

Параметры: среднее значение = последняя цифра номера зачетки,

стандартное отклонение = предпоследняя цифра номера зачетки, если она не равна нулю. Если равна, то первая не равная нулю цифра.

Представить выборку

• в первичном виде,

• в виде вариационного ряда,

• в виде группированного ряда.

• Указания к пункту 1.

Метод получения: моделирование в Excel.

Сервис – Анализ данных - Генерация случайных чисел

Если в меню «Сервис» отсутствует «Анализ данных», то открыть его:

Сервис – Надстройки – Пакет анализа (отметить галочкой) - ОК

Пример определения параметров.

Номер зачетки 630839.

Объем выборки равен 100+ 29 = 139.

среднее значение = 9, стандартное отклонение = 2.

Если номер зачетки 264701, то стандартное отклонение = 7.

Если номер зачетки 563002, то стандартное отклонение = 3.

• Первичный вид выборки:

записывается последовательность промоделированных значений в порядке получения.

• Вариационный ряд:

последовательность чисел, расположенная в порядке возрастания их величин.

• Группированный ряд (при . объеме выборки, равном 139).

1. Определим размах выборки R - разность между максимальным и минимальным значениями элементов выборки

2. Определим число интервалов:

2^k−1 ≈ n

n = 139

27 = 128 < 139 < 256 = 28

7 < k − 1 < 8

8 < k < 9; пусть k = 8 3. Определим длину интервалов:

Таблица 1.

Группированный ряд (общий вид таблицы)

№	интервалы	ni
1
2
3
4
5
6
7
8

2. Задание: нахождение числовых характеристик выборки.

• выборочного среднего,

• выборочной дисперсии,

• исправленной выборочной дисперсии,

• среднеквадратичного отклонения,

• исправленного среднеквадратичного отклонения,

• выборочных начальных моментов порядка 2, 3, 4,

• выборочных центральных моментов порядка 3, 4,

• выборочного коэффициента асимметрии,

• выборочного коэффициента эксцесса,

• моды,

• медианы,

• выборочных квантилей порядка 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9.

• Указания к пункту 2.

1. Выборочным средним называют среднее арифметическое значение признака выборочной совокупности.

2. Выборочной дисперсией S² называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения

3. Исправленная выборочная дисперсия

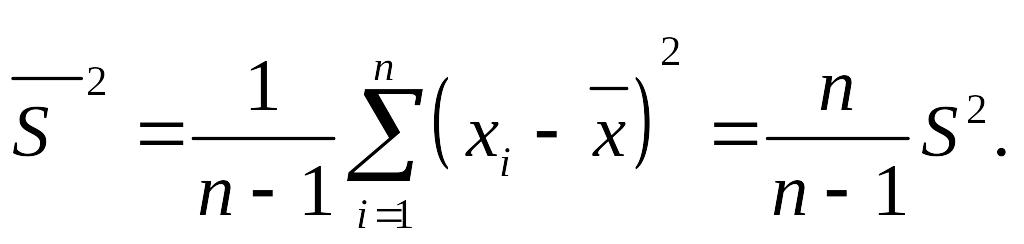
4. Среднеквадратичное отклонение - квадратный корень из выборочной дисперсии. Используется для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения

5. Исправленное среднеквадратичное отклонение равно квадратному корню из исправленной дисперсии.

6. Выборочные начальные моменты порядка 2, 3, 4

Выборочный начальный момент 1 порядка:

7. Выборочные центральные моменты порядка 3,4

Выборочный центральный момент 1 порядка:

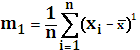
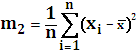− дисперсия

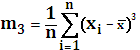
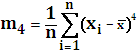
8. Выборочный коэффициент асимметрии

9. Выборочный коэффициент эксцесса

10.Выборочная мода

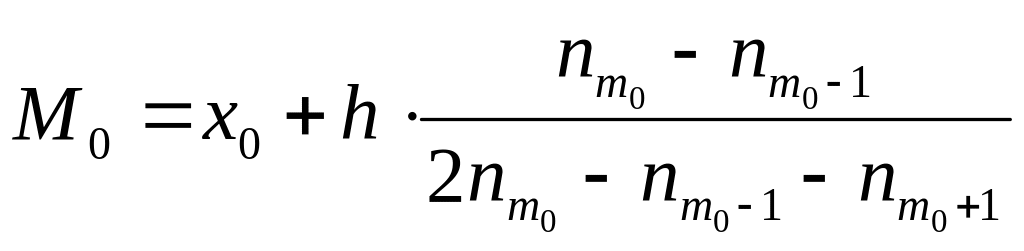
11. Выборочная медиана

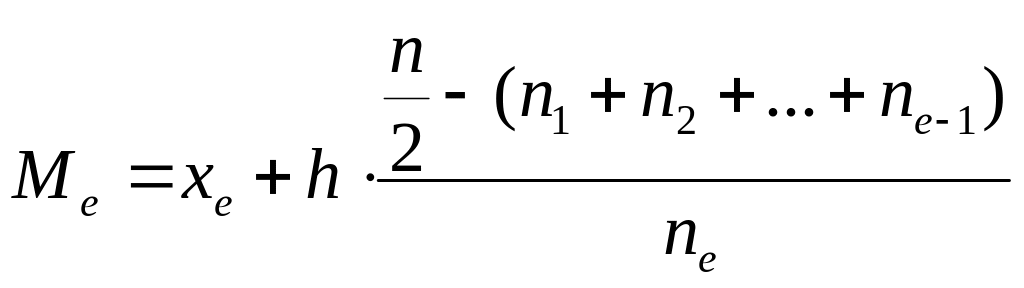
12. Выборочная квантиль порядка q

3. Задание: графическое представление выборки:

• группировка данных,

• гистограмма частот,

• полигон частот,

• кумулята,

• эмпирическая функция распределения.

• Указания к пункту 3.

• Группировка данных. Составим таблицу частот (табл.2.).

• Таблица 2.

Таблица частот группированной выборки

(вид таблицы)

k	Xi	Xi+1	ni	Xср	n*i	ni/h	ni*/n
1
2
3
4
5
6
7
8							1

• Гистограмма частот – это фигура, составленная из прямоугольников, построенных на интервалах группировки как на основаниях, так, что высота i–го прямоугольника равна n_i/h для гистограммы частот, и n_i/nh для гистограммы относительных частот.

• Полигон частот – ломаная, соединяющая середины верхних оснований гистограммы.

• Кумулята относительных частот – это ломаная, соединяющая точки с координатами (x_i, n_i*/n). Кумулята частот соединяет точки с координатами (x_i,n_i*). Кумулята дает представление о графике функции распределения.

• Эмпирическая функция распределения F*_n(x) в каждой точке x равна числу элементов выборки, меньших x, деленному на n.