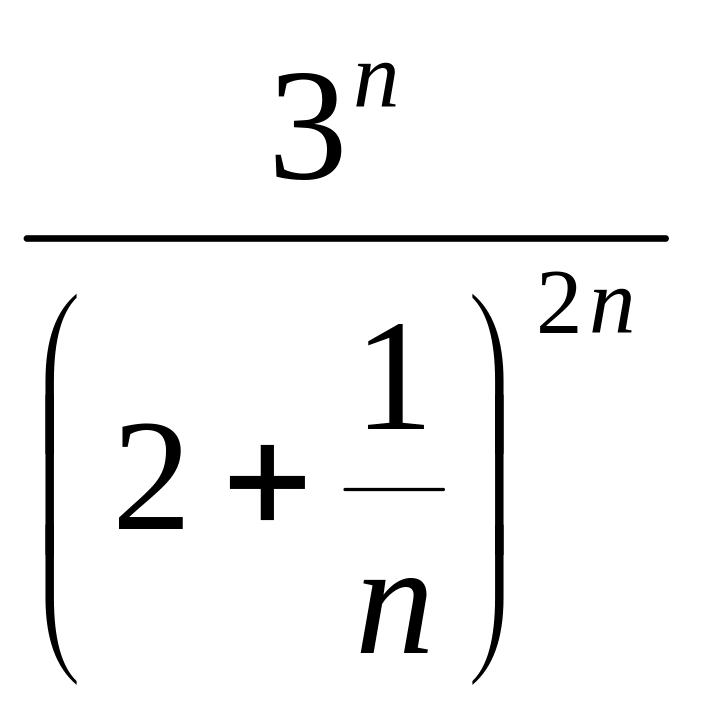Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методич указания ряды.doc

Скачиваний:

2

Добавлен:

01.05.2025

Размер:

1.43 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Задания к типовому расчету «Ряды и их приложения»

1. Определить, сходится ли числовой ряд с заданным (под номером N₁) общим членом .

Исследовать на абсолютную и условную сходимость знакочередующийся ряд с заданным (под номером N₂) общим членом .
Найти радиус сходимости степенного ряда с заданным (под номером N₃) коэффициентом . Проверить сходимость (абсолютную и условную) этого ряда в концах интервала сходимости.
Разложить данную (под номером N₄₎функцию в ряд Тейлора в заданной точке х₀ и определить радиус сходимости полученного ряда.
Вычислить приближенное значение (заданной под номером N₅)функции в данной точке х, используя разложение этой функции в ряд Маклорена и, отбросив все слагаемые, начиная с х⁶. Результат округлить до 10^-3 и сравнить с точным значением функции, вычисленным непосредственно или при помощи таблиц.
Ответить на теоретический вопрос, соответствующий (при 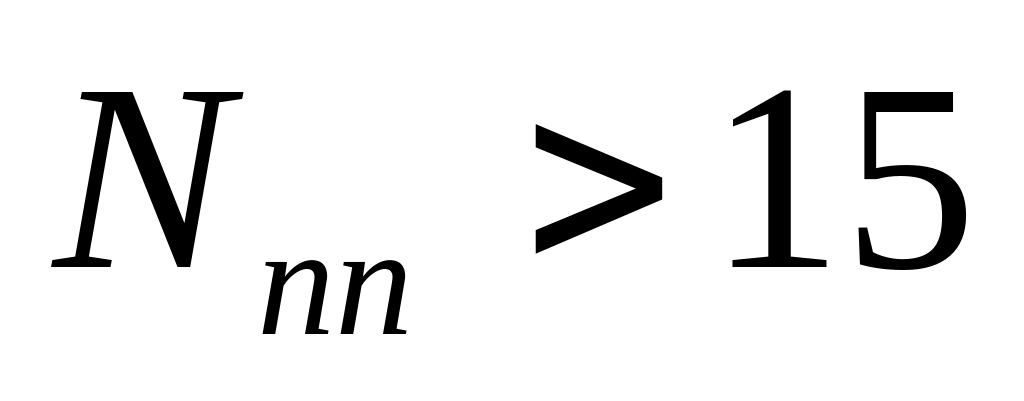взять ).

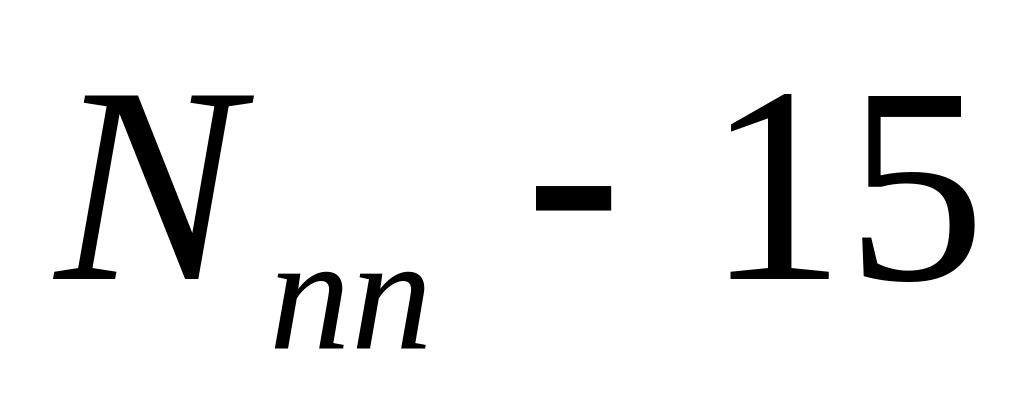Теоретические вопросы к типовому расчету «Ряды»

Понятие числового ряда и его сходимости. Примеры.
Необходимый признак сходимости рядов. Пример его недостаточночти.
Признак сравнения рядов с неотрицательными членами.
Признаки Даламбера и Коши.
Интегральный признак. Сходимость ряда: .
Абсолютная и условная сходимость рядов с членами любого знака.
Признак Лейбница.
Радиус и интервал сходимости степенного ряда.
Почленное дифференцирование и интегрирование степенного ряда.
Ряд Тейлора.
Ряд Маклорена. Разложение функции .
Разложение в ряд Маклорена функци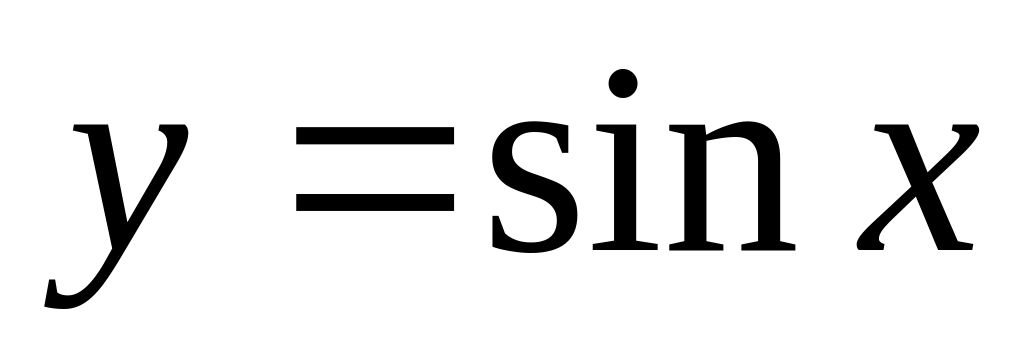й и .
Разложение в ряд Маклорена функции .
Разложение в ряд Маклорена функции .
Применение степенных рядов к приближенным вычислениям.

Таблицы выбора общего члена и функций

N п/п	I
N п/п	N₁	N₂	N₃	N₄	X₀	N₅	X
1	27	32	68	108	-1	104	0,2
2	58	33	69	94	0,25	112	-0,3
3	59	34	70	129		102	-0,03
4	22	49	29	96	-0,125	111	-0,2
5	3	50	30	127		100	3
6	7	51	31	99	8	110	-0,2
7	11	52	35	125		98	0,5
8	28	4	71	101	64	109	0,3
9	66	5	72	124		97	-4
10	21	53	73	103	64	108	0,3
11	15	54	74	121		95	0,1
12	60	6	75	105	10	129
13	61	8	76	120		93	-0,2
14	62	9	77	78	0,5	128
15	63	36	10	117		91	-0,5
16	64	37	12	80	-2	127
17	65	38	13	116	3	90	0,5
18	67	39	14	83	-4	126
19	49	58	16	115	1	88	0,2
20	50	24	17	86	4	125
21	51	59	18	114	3	87	0,2
22	52	25	19	89	4	123
23	53	60	20	113	1	85	0,25
24	54	36	22	92	2,25	122
25	55	61	13	112	1	84	-0,2
26	56	62	7	94	49	119
27	57	63	11	111	-3	82	0,1
28	23	51	40	96	27	118
29	1	52	44	110	-3	81	0,4

N п/п	II
N п/п	N₁	N₂	N₃	N₄	X₀	N₅	X
1	22	60	47	115	-1	105	0,3
2	3	61	48	108	-2	104	-0,1
3	7	62	29	114	-8	102	0,1
4	11	63	30	115	3	100	-2
5	28	49	68	110	-1	98	0,4
6	66	50	69	116	-1	97	4
7	23	64	31	117		95	0,2
8	1	65	35	111	3	93	-0,25
9	2	67	71	120		91	1
10	4	51	72	121		90	0,75
11	5	52	73	112	-2	88	-0,1
12	6	53	74	124		87	0,4
13	54	8	75	125		85	-0,2
14	55	9	76	113	2	84	1
15	56	10	77	127		82	0,3
16	57	12	70	129		81	-0,5
17	13	32	49	105	6	127
18	14	33	50	103	-27	126
19	16	34	51	101	-27	125
20	17	36	52	99	-0,125	123
21	37	18	53	96	64	122
22	38	19	54	94	9	119
23	39	20	55	92	9	118
24	24	40	13	89	16	116	0,4
25	25	41	14	85	25	115	-0,1
26	26	42	16	83	-3	112	0,3
27	21	43	56	80	4	111	0,3
28	15	44	57	78	-0,5	110	0,2
29	58	45	17	105	3	109	-0,2

N п/п	III
N п/п	N₁	N₂	N₃	N₄	X₀	N₅	X
1	27	32	68	78	0,1	129
2	58	33	69	80	2	128
3	59	34	70	83	3	127
4	60	21	29	86	16	126
5	61	15	30	89	0,16	125
6	62	20	31	92	0,25	123
7	63	19	35	94	4	122
8	64	18	71	96	-8	119
9	28	17	72	99	27	118
10	66	16	73	101	0,125	116	-0,6
11	22	24	74	103	-8	115	0,2
12	3	25	75	105	0,5	112	-0,4
13	7	26	76	78	-5	111	-0,3
14	11	36	77	80	-0,5	110	-0,1
15	37	23	53	110	2	100	2
16	1	54	38	124		98	-0,4
17	39	55	2	111	-2	97	-2
18	4	56	40	108	1	95	-0,2
19	41	57	5	112	2	93	0,25
20	6	42	24	129		91	-1
21	43	8	25	113	6	90	-1
22	9	44	26	127		88	0,1
23	45	10	37	114	4	87	0,5
24	12	46	1	115	-3	85	-0,1
25	47	13	39	125		84	0,5
26	14	48	4	116	2	82	0,2
27	49	16	41	124		81	0,6
28	17	50	6	117		79	0,25
29	51	18	43	121		106	-0,3

N п/п	IV
N п/п	N₁	N₂	N₃	N₄	X₀	N₅	X
1	27	39	68	129		79	0,2
2	24	44	69	83	-2	109	0,2
3	62	34	70	86	9	123
4	34	20	29	89	0,25	108	-0,4
5	22	40	30	92	4	122
6	43	21	31	94	16	129
7	11	57	35	96	-64	119
8	56	15	71	99	-8	128
9	3	55	72	101	-8	118
10	7	54	73	103	27	127
11	53	2	74	105	2	116	0,3
12	9	24	75	78	2	126
13	25	14	76	80	3	115	-0,2
14	19	26	77	83	0,5	125
15	28	19	32	92	9	112	-0,2
16	66	33	18	127		81	0,1
17	27	34	17	125		102	-0,1
18	58	16	36	113	-6	82	-0,1
19	60	38	14	124		104	-0,2
20	62	39	13	112	-3	84	-0,5
21	63	12	40	121		106	-0,2
22	65	10	41	111	1	85	0,2
23	64	42	9	120		107	-0,05
24	67	8	37	110	0,5	87	-0,4
25	61	6	43	117		79	-0,2
26	59	44	5	108	0,2	88	0,3
27	49	45	4	116	-2	81	-0,2
28	50	46	2	110	1	90	-0,5
29	51	1	47	115	0,5	82	-0,2

Список a_n

1

11

21

31

41

51

61

71

2

12

22

32

42

52

62

72

3

13

23

33

43

53

63

73

4

14

24

34

44

54

64

74

5

15

25

35

45

55

65

75

6

16

26

36

46

56

66

76

7

17

27

37

47

57

67

77

8

18

28

38

48

58

68

9

19

29

39

49

59

69

10

20

30

40

50

60

70

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.09.2019214.53 Кб6Метод-ка с исправл.doc
#
01.03.2025537.09 Кб3метод. по практике.doc
#
17.04.2015323.58 Кб20метод. указания Russia Novosibirsk.doc
#
01.04.2025168.96 Кб4Метод. указания Плетнев18 февр.doc
#
27.11.201972.19 Кб12Методика проведения SWOT для студентов.doc
#
01.05.20251.43 Mб2методич указания ряды.doc
#
01.07.20254.72 Mб0Методические указания СЖД 2009 Гренкевич_Карас...doc
#
01.05.20254.08 Mб1Методические ук по ММ.doc
#
27.04.2019333.31 Кб191Методические указания в авар.ситуациях Лемешко....doc
#
09.11.2019237.57 Кб10методические указания Джаманов И.М..doc
#
01.04.2025180.74 Кб0Методические указания к РГР.doc