Зависимые и независимые св

СВ Х иY называются независимыми, если событие Х<x и Y<y являются независимыми при любых значениях X и Y. Если же эти события при некоторых значениях X и Y являются зависимыми, то и СВ X и Y являются зависимыми.

Необходимое и достаточное условие независимости 2-х СВ:

Для того, чтоб СВ X и Y были независимые необходимо и достаточно, чтоб функция распределения системы была равна произведению функций распределений составляющих:

F(x,y)=F1(x)F2(y)

Доказательство:

Необходимость:

Считаем, что Х и Y независимые. Тогда по определению P(X<x,Y<y)=P(X<x)P(Y<y), но это тоже самое F(x,y)=F1(x)F2(y)

Достаточность:

Считаем, что F(x,y)=F1(x)F2(y) выполняется. Докажем, что Х и Y независимы. По определению F(x,y)=P(X<x,Y<y)=F1(x)F2(y)=P(X<x)P(Y<y), т.е. вероятность произведения является равной произведения вероятностей, значит Х и Y независимы.

Следствие:

Для того, чтоб СВ Х и Y были независимыми необходимо и достаточно, чтоб плотность распределения системы была равна произведению плотностей распределения составляющих f(x,y)=f1(x)f2(y)

Доказательство:

Необходимость:

Считаем, что Х и Y независимые. Тогда F(x,y)=F1(x)F2(y). Дважды продифференцируем обе части

Достаточность:

Считаем, что f(x,y)=f1(x)f2(y). Докажем, что Х и Y независимые СВ. Дважды проинтегрируем обе части

И получается

F(x,y)=F1(x)F2(y), по теореме они независимые.

11) Числовые характеристики двумерных св. Коэффициент корреляции и его свойства.

Числовыми характеристиками системы СВ являются математическое ожидание, дисперсия, начальный и центральный моменты.

А) Математическое ожидание системы:

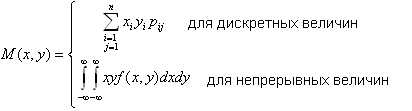
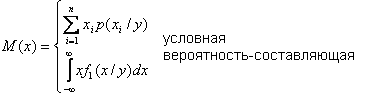
В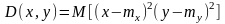 ) Дисперсия системы 2-х СВ.

Математическое ожидание от произведения квадратов отклонения СВ.

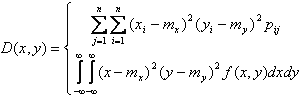
С) Моменты

- начальный момент порядка k+s называется математическое ожидание от

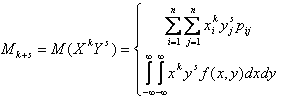
Ч астные случаи:

-центральным моментом называется математическое ожидание от произведения отклонении Х в степени k и Y в степени s

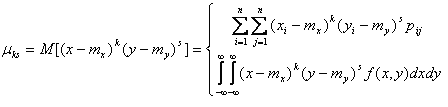
Частные случаи:

Теорема: Корреляционный момент 2-х независимых СВ равен 0, а если СВ являются зависимыми, то корреляционный момент не равен 0.

Д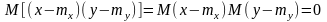 оказательство: По определению 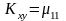. Если СВ независимы, то и тоже независимы. Тогда по свойству математического ожидания:

Корреляционный момент 2-х зависимых величин не обращается в нуль, т.е. между ними существует некоторая связь.

В еличины X и Y для которых корреляционный момент равен 0 называется некоррелярованными. Величины X и Y для которых корреляционный момент не равен 0 называется коррелярованными.

К оэффициент корреляции называется отношение корреляционного момента к произведению средне квадратичных отклонений составляющих

Свойства:

, тогда | | 1

Е сли >0 –положительная корреляционная связь

Если <0 – отрицательная корреляционная связь

12) Нормальный закон распределения на плоскости.

Закон распределения системы случайных величин называется нормальным, если плотность распределения f(x,y) равна:

Если X и Y независимы, то rxy=0. Если a=b=0 и σx=σy=0. И если , то

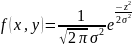
Распределение Реллея: