1)Элементы комбинаторики – изучает число элементов во множестве
Перестановки – множество из n элементов отличающиеся друг от друга местораположением
=n!
– число перестановок
Размещение – соединение отличающееся либо самими элементами либо их порядком.
= n(n-1)(n-2)…
[n-(m-1)]
Сочетание – соединение из nэлементов, отличающихся элементами.
=
=
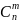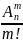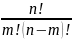
Событие(явление)-любой результат опыта.События обозначают заглавными буквами A,B,C.Его различают на:
1)Достоверное, которое обязательно произойдет. P(A)=1
2) Невозможное, которое заведомо не произойдет.P(A)=0
3)Случайное, которое в результате опыта может произойти, а может и не произойти
Совместные события-если появление одного из них вызывает появление другого.
Несовместные – если появление одного из них исключает появление другого.
Зависимые, при них появление одного из них зависит произошло или не произошло второе.
Независимые, появление одного не зависит от появления другого.
Равновозможные события, если нет основания считать , что одно из них более возможно чем другое.
Единственно возможное – если в опыте,появление только одного из них является возможным
Элементарные события – которые нельзя разложить на более простые.
Полной группой событий называется событие которые при проведении опыта являются несовместные и единственно возможными, т.е. обязательно произойдет одно из них.
Алгебра событий
,
,
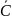– противоположные события.
Св-ва:
А
+
=
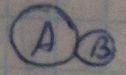достоверное
А
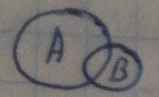+B
= B+A
AB=BA
A+(B+C)=(A+B)+C=A+B+C
(A+B)C = AC+BC
A+ =
невозможное
Классическое опред.:
Вероятностью событий Aравно:
P(A)=
, m
nотношению
числа благоприятствующих исходов
испытаний к числу всех равновозможных
и единственно возможных элементарных
исходов испытаний. 0
P(A)
1
Статистическое определение:
Относительная
частота события A.W(A)
=
Вероятность это предел частоты по кол-ву экспериментов отношение испытаний в которых события произошло к числу всех испытаний.
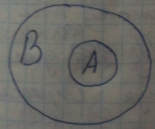
Геометрическое определение:
P(A)=
Мера области A к мере области B– геометрическая вероятность.
3)Формула полной вероятности
Событие
А может произойти если произойдет
событие
входящее в полную группу (L=1,K).
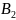A=
A+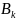
A+..+
A
P(A)=
(
A)+
(
A)+..
(
A)
P(A)= ( )P(A)+ ( )P(A)+.. ( )P(A)-фор-ла полной вероятности
Формула Бейеса
(
)-событие
А произошло по какой-то гипотезе
,
А и
-зависимые
события.
( А)= (А )=
(AB)=
(A)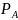
(B)=
(B)
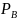(A)
(B)=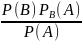
(
)=
-фор-ла
Бейеса (P(A)опред
по фор-леполной вер-сти).
Вероятность появления 1-го события
Если
имеются события
(независимые
между собой) они назыв независимы в
совокупности ,если каждое из них не
зависит от остальных.
P:А
зависит от
,а
от
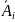:q
+A=Ω
P( +A)=P(Ω)
P(A)+P( )=1
P(A)=1-
P(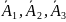
)=1-P(
,..
)=1-
P(
)P(
)P(
)..P(
)
4) Независимые опыты – опыты, когда результат одного не зависит от результата второго.
Схема
Бернулли: если результат одного не
зависит от результата другого и при
проведении опыта возникает событие A
или A̅.
Найти вероятность того, что при n
испытаниях событие произойдет m
раз, если при каждом испытании вероятность
события одинакова p.
Pn(m).
Пусть n=3,
найти P3(2):
AAA̅,AA̅A,A̅AA
– p^2q,p^2q,p^2q.
P3(2)=3p^2q=
Pn(m)=
– формула бернулли. Вероятность того
что в n
испытаниях произойдет m
событий равно числу сочетаний из n
по m
умноженной на вероятность в степени m
и умножен. На вероятность не происхождения
события в cтепениn-m.
(p+q)^n=1,
(p+q)^n=p^n+n*p^(n-1)*q+
+…+q^n=1
– биноминальное распределение.
Если
n-большое,
а p-малое,
то Pn(m)
=
=//np=
;
p=
;=
(1-1/n)(1-2/n)…(1-(m-1)/n)*
^m)/m*(1-
)^(-m)
LimPn(m)=
,
Pn(m)=
-формула
Пуасонна
Локальная и интегральная теоремы Лапласа:
Локальная: если вероятность появления события постоянна и не равна 0 или 1, то вероятность того что в n испытаниях событие произойдет ровно m раз равна значению функции.
Pn(m)
=
,
где
=
,
x=
Теорема интегральная: если вероятность появления события в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что это событие в n испытаниях произойдет от m1 до m2 раз приближенно равна:
Pn(m1,m2)=
где x1=
x2=
ȹ(x)=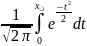
– функция Лапласа нечетная ȹ(-x)=-
ȹ(x)
Pn(m1,m2)=
Найвероятнейшее число появления события.
Пусть m0 –число найвероятнейших событий m0-1<m0<m0+1
1 P(m0)>P(m0-1)
2 P(m0)>P(m0+1)
1
>
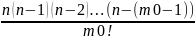pm0qn-m0>
(n-m0+1)p>m0q
Np-m0p+p>m0q np+p>= m0
2
>
pm0qn-m0>
q(m0+1)>np-m0p m0q+q>np-m0p
m0>np-q np-q<=m0<=np+pоценкаm0
Вероятность отклонения относительной частоты от вероятности в одном испытании
P(|m/n-p|<ε)
По интегральной теореме Лапласа
Pn(m1,m2)=
,
x1=
x2=
|(m-np)/n|<ε
-ε<(m-np)/n<ε
P(|m/n-p|<ε)=
5)Случайная величина – величина которая при испытании получит значение но заранее неизвестно какое именно.
Случайные величины: дискретные, непрерывные.
Дискретной называется случайная величина, которая принимает конкретные изолированные значения. Непрерывной называется случайная величина, значение которой принадлежит некоторому интервалу (a,b).
Законом распределения случайных величин называется соотношение между возможными значениями этой величины и соответствующей ей вероятности.
Законы распределения :
Т
абличный:
X,Y,Z
– совокупность, x,y,z–
значения
X |
x1 |
x2 |
|
xk |
P |
p1 |
p2 |
|
pk |
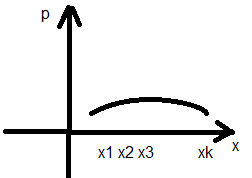
Графический многоугольное распределение
Аналитический способ: F(x) – интегральная функция распределения
Интегральной функцией распределения называется функция того, что случайная величина X примет значения меньше, чем x. F(x)=P(X<x)
Свойства интегральной функции:
1) F(x)>=0; 2) 0=<F(x)=<1; 3) F(x) – возрастающая; 4) F(∞)=1, F(-∞)=0; 5) P(a<x<b)=F(b)-F(a)
Доказательство:
3) x2>x1; X<x2=X<x1+x1=<X=<x2; F(x2)=F(x1)+P(x1=<X=<x2); F(x2)-F(x1)= P(x1=<x=<x2)>=0.
4) Из определения любое значение x будет меньше ∞(достоверно) и ни одно меньше -∞(невозможно).
Вероятность того, что непрерывная случайная величина примет конкретное значение равно нулю. Функция распределения работает как для дискретных, так и для непрерывных величин. Если случайная величина непрерывна то и функция непрерывна.
7) Закон распределения дискретных СВ (биномиальный,Пуасонна).
- Биномиальный:
- Закон распределения Пуассона:
,
.
8) Закон равномерного распределения
Равном. Законом распределения называется распределение при котором плотность является величиной постоянной.
F(x)=c
cx|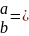
c(b-a)=1P.S.
это
не деление!!!!!!
C=1/b-a
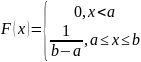----плотность
распределения
F(x)=
Показательный закон
Показательный – закон, если плотность распределения F(x) выражается
P.S.
это
не деление!!!!!!
Нормальный закон (Закон Гаусса)
Ему подчиняются ошибки измерений распределения нагрузочных режимов
Нормальный закон-распределение, если плотность распределений равно F(x) равна:
a,
-const
Найдём матем ожидание
=t;
x-a=
;dx=
dt
P.S.
сокращается!!!!
=
Интеграл Пуассона
Вероятность
попадания случайной величины в интервал
(
):
Вероятность того, что случ величина принадлежит заданному интервалу.
Но прежде рассмотрим вероятности отклонения случ величины от матиматич ожидания на величину Е:
P(
)
-E<x-a<E
a-E<x<a+E
P(
)=Ф(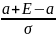
)-
=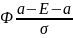