Лабораторная работа № 11 «Исследование монохроматических аберраций оптической системы»

7. Контрольные вопросы

1. Каким образом возникают действительные изображения в оптических системах?

2. В чем сущность теории идеальной оптической системы? Какими параметрами характеризуется идеальная оптическая система?

3. Приведите пример графического построения изображений в оптической системе, используя ее кардинальные точки.

4. Какой метод определения кардинальных точек рекомендуется в предлагаемой лабораторной работе?

5. Поясните, каким образом явление дифракции света ограничивает разрешающую способность оптических систем.

6. Kaкyю величину принимают в качестве меры разрешающей способности оптических систем?

7. В чем состоит метод практического определения разрешающей способности, используемой в лабораторной работе?

Лабораторная работа № 12 «Исследование хроматических аберраций оптической системы»

7. Контрольные вопросы

1. Каким образом возникают действительные изображения в оптических системах?

2. В чем сущность теории идеальной оптической системы? Какими параметрами характеризуется идеальная оптическая система?

3. Приведите пример графического построения изображений в оптической системе, используя ее кардинальные точки.

4. Какой метод определения кардинальных точек рекомендуется в предлагаемой лабораторной работе?

5. Поясните, каким образом явление дифракции света ограничивает разрешающую способность оптических систем.

6. Kaкyю величину принимают в качестве меры разрешающей способности оптических систем?

7. В чем состоит метод практического определения разрешающей способности, используемой в лабораторной работе?

Лабораторная работа № 13

«Дифракция Фраунгофера»

1. Цель и задачи работы

Ознакомление с дифракционными картинами различных типов.

2. Основные теоретические положения

Р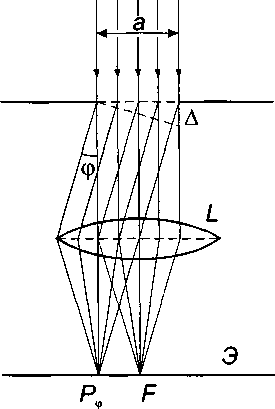 ассмотрим дифракцию плоской монохроматической волны от щели. Щелью будем называть прямоугольное отверстие, ширина которого во много раз меньше его длины. Обозначим ширину щели а (рис. 1).

Световая волна длиной  падает нормально к плоскости щели. За щелью установлена собирательная линза L, в фокальной плоскости которой находится экран Э. Параллельный пучок лучей, пройдя через щель, дифрагирует под разными углами вправо и влево от первоначального направления. Линза собирает параллельные пучки дифрагированных лучей в соответствующих точках экрана Э. Тип дифракции, при котором рассматривается дифракционная картина, образованная параллельными лучами, получил название дифракции в параллельных лучах, или дифракции Фраунгофера.

Рис. 1

В случае прямоугольного отверстия дифракционная картина будет описываться формулой

где a, b – размеры отверстия,

,  – угловая координата точки в дифракционной картине,

, ,

где x, y – координаты в плоскости экрана, на котором наблюдается дифракционная картина,

L – расстояние от плоскости отверстия, на котором дифрагирует световая волна, до экрана, на котором наблюдается дифракционная картина,

, E – полная энергия, падающая на отверстие,

D = 4ab – площадь отверстия.

Расчет дает формулу распределения интенсивности света на экране Э в зависимости от угла дифракции в виде

/ •

( — sm

л

2 , ~"

(1)

sm

1<р = I О

ПО . ₂

(—sin <р) л,

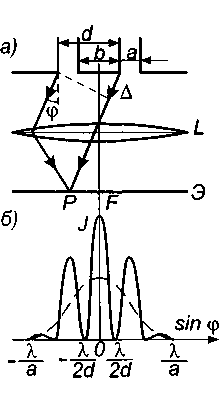
где Ь - интенсивность света в середине дифракционной картины (в направлении ф=0); I - интенсивность света в точке, положение которой определяется данным значением угла ф. При значении угла дифракции ф, удовлетворяющего условию

sin<p=k/l,, asinp^kA, (2)

Я

б)

Рис.2

где К=±1, 2, 3, ..., интенсивность света равна нулю. Последнее условие и количественные соотношения можно получить при решении задачи о дифракции на щели методом графического сложения амплитуд. Разобьем открытую часть волновой поверхности на ряд узких параллельных полосок равной ширины. Каждую из этих полосок можно рассматривать как источник волн одинаковой амплитуды и фазы. Выражая амплитуды каждой полоски векторами равной длины, найдем результирующую амплитуду, пользуясь графическим методом сложения амплитуд. Результаты при разных углах дифракции ф представлены на рис.2. При ф=0 (рис.2,а), т.е. в фокусе линзы L, амплитуда колебаний А₀ будет максимальной. В направлении, при котором крайние

2А

амплитуда равна

полоски отличаются по фазе на я (А=—), результирующая (рис.2,6), так как последняя равна диаметру полуокружности, длина

которой aq. В направлении, при котором крайние полоски отличаются по фазе на 2я (Д=А), результирующая амплитуда обращается в нуль (рис.2,в). Амплитуда равна нулю во всех случаях, когда разность хода между крайними лучами А равна А,, 2А, ЗА, ..., kA, т.е.

Я 2Я минимумы освещенности соответствуют направлениям sin <p = —, - ..., где k-целое число,

a a

так как Л = a sin (p.

Распределение освещенности в фокальной плоскости линзы L представлено на рис.3. Центральная светлая полоса (максимум нулевого порядка) занимает область между ближайшими правыми и левыми минимумами, т.е. область

между sin <р = и sin#> = —. Интенсивность света 1₀

а а

определяется квадратом А₀. Следующие максимумы значительно уступают по величине центральному.

амплитуда колебаний

Действительно, при

А \ =

(рис.2,г), интенсивность первого максимума 7 i = ( — )²/ о или Ii=0,045Io. п Ъп

Аналогично можно найти и интенсивности остальных максиммов. Расчеты

2 А о 3

можно нати и интенсивности остальных максимумов.

показывают, что интенсивности центрального и следующих максимумов относятся как

1:0,045:0,016 и т.д.

Рассмотрим дифракцию от двух параллельных щелей одинаковой ширины а и расположенных на расстоянии b друг от друга. Дифракционная картина наблюдается в фокальной плоскости линзы L. (рис.4, а). На экран со щелями падает плоская монохроматическая волна длиной А. Положение дифракционных максимумов и—ТЯйнимумов от одной щели не зависит от ее положения, а определяется направлением дифрагированных лучей. Это значит, что перемещение щели параллельно самой себе не приводит к изменению дифракционной картины. Следовательно, картины, создаваемые каждой щелью в отдельности будут совершенно одинаковыми.

Рис.4

Результирующую картину можно определить путем сложения этих двух картин о учетом интерференции волн, идущих от каждой из щелей. Очевидно, что в тех направлениях, в которых ни одна из щелей света не

дает, н£ будет света и при двух параллельных щелях. Условие

минимума интенсивности a sin <p= kA, где к=±1, 2, 3, ... , выполняется и в данном случае.

Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями,

взаимно уничтожаются. Возникают добавочные минимумы. Они будут наблюдаться в тех

1,3. 2т +1 .

направлениях, которым соответствует разность хода — Я, — Я, ... , - Я для волн,

идущих от соответственных точек (отстоящих на расстоянии а+b) обеих щелей. Такие

Я направления определяются (см.рис.4) условием Д(а +b )sin (р=(2т +1)—, где т=±0, 1, 2,

3, ... . В направлениях, определяемых из условий (a +b )sin <р = 0, A, 2A, ...тА, где т=±0, 1, 2,

Действие одной щели усиливает действие другой. Этим направлениям соответствуют максимумы интенсивности. Расстояния между первичными минимумами (от одной щели) зависит от ширины щели а . Если а «(а +Ь), то между двумя первичными минимумами может

расположиться несколько минимумов и максимумов. Кривая на рис.4,6 показывает распределение интенсивностей света при дифракции на двух параллельных щелях.

Если ширина щели а значительно меньше расстояния от щели до экрана, дифракция Фраунгофера будет иметь место и при отсутствии линзы между щелью и экраном (падающая на щель волна должна быть плоской). В этом случае лучи, идущие в точку Р от краев щели, будут практически параллельны, так что все полученные ранее результаты остаются справедливыми.

Измерив на опыте по дифракционной картине от узкой щели ширину центрального максимума и зная длину волны источника света, можно определить ширину щели. По картине дифракции от двух параллельных узких щелей, зная длину волны источника и ширину каждой щели, можно определить расстояние между ними.

• Одномерная дифракция Фраунгофера на вертикальной щели по мере ее расширения слева направо.

• Нулевой максимум наиболее яркий и вдвое шире побочных максимумов.

• Размер области дифракционного расплывания обратно пропорционален ширине щели.