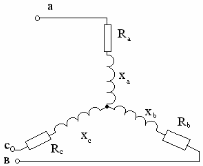
3.2 Задача

В трехфазную трёхпроводную цепь с симметричным линейным напряжением Uл включены звездой сопротивления. Определить фазные и

линейные токи, активную мощь всей цепи и каждой фазы в отдельности. Построить векторную диаграмму токов и напряжений.

Дано: Uл = 220 В,

Rа = Rb = Rc = 15,6 Ом,

xa = xb = xc = 7 Ом.

Решение:

: 127[В] = 127 [В]*1,7

Zа = Zb = Zc = (Ra^2 + Xa^2 )½=(243,36+49) ½=17,1 [Ом]

Iл = Iф: Iа = Ib = Iс = Ua /Za = 220/17,1 = 7,4 [А];

Iа+ Ib+ Iс= 0

Cosφa= Rа/ _Zа= 0,9

Cosφb= Rb/ _Zb= 0,9

Cosφc= Rc/ _Zc= 0,9

P = Pa+Pb+Pc:

Pa = Ua*Ia*сosφa = 127*7,4*0,9 = 846[Вт];

Pb = Ub*Ib*cosφb = 127*7,4*0,9 = 846[Вт];

Pc = Uc*Ic*cosφc = 127*7,4*0,9 = 846[Вт];

P = 846+846+846 = 2538[Вт].

Ответ: Iа=7,4[А];

Ib=7,4[А];

Iс=7,4[А];

Pa=846[Вт];

Pb=846[Вт];

Pc=846[Вт];

P=2538[Вт].

4.Трансформаторы

4.1 Теоретическая часть

Действующие значения ЭДС, наводимые в первичной и вторичной обмотках, определяется по следующим формулам:

Е₁=4,44fω₁Ф_m, (4.1)

Е₂=4,44fω₂Ф_m, (4.2)

где Е₁ и Е₂ - ЭДС первичной и вторичной обмоток, В;

f- частота переменного тока, Гц;

Ф_m- амплитудное значение магнитного потока сердечника, Вб;

ω₁ и ω₂- число витков первичной и вторичной обмоток.

ЭДС рассеяния в первичной и вторичной обмотках трансформатора:

E_1рас= -jx_1расI₁, (4.3)

E_2рас= -jx_2расI₂, (4.4)

где x_1рас=2πfL_1рас и x_2рас=2πfL_2рас – индуктивные сопротивления рассеяния первичной и вторичной обмоток;

L_1рас и L_2рас – индуктивности первичной и вторичной обмоток, обусловленные магнитными потоками рассеяния.

Номинальная мощность трансформатора однофазного:

S_н= U_1н* I_1н, (4.5)

где U_1н, I_1н – номинальные напряжения и ток первичной обмотки.

Номинальная мощность трехфазного трансформатора:

S_н=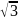 *U_1лн* I_1лн , (4.6)

где U_1лн , I_1лн – линейные напряжения и ток первичной обмотки.

Номинальный ток вторичной обмотки для однофазного трансформатора:

I_2н= S_н/ U_2н , (4.7)

где U_2н – номинальное напряжение вторичной обмотки.

Номинальный ток вторичной обмотки для трехфазного трансформатора:

- линейный ток - I_2лн=S_н/ *U_2лн (4.8)

- фазный ток – I_2н=S_н/3*U_2н , (4.9)

где U_2лн, U_2н – линейное и фазное напряжения вторичной обмотки.

Потери мощности холостого хода расходуются на нагрев стали магнитопровода и для однофазного трансформатора рассчитываются по следующей формуле:

P_x=P_ст=I_x*U_1н*cos φ _x, (4.10)

для трехфазных трансформаторов:

P_x=P_ст=3*I_x*U_1н*cos φ _x, (4.11)

где I_x – ток холостого хода;

φ _x – сдвиг по фазе между векторами U_1н и I_x.

Ток холостого хода обычно задается в процентах от номинального значения тока первичной обмотки:

I_x%=I_x/I_1н*100% (4.12)

Полное сопротивление однофазного трансформатора при холостом ходе равняется полному сопротивления намагничивающей цепи:

z_x=U_1н/I_x (4.13)

Активное сопротивление трансформатора при холостом ходе:

r_x=z_x*cos φ _x=P_x/I_x² (4.14)

Реактивное сопротивление трансформатора при холостом ходе:

x_x=z_x*sin φ _x= (4.15)

Потери мощности при коротком замыкании расходуются на нагрев меди обмоток и для однофазного трансформатора определяются так:

P_к=P_мед=I²_1н*R₁+I²_2н*R₂, (4.16)

где R₁ и R₂ – активные сопротивления первичной и вторичной обмоток.

Напряжение первичной обмотки, при котором токи в обмотках короткозамкнутого трансформатора равны номинальным, называется номинальным напряжением короткого замыкания U_кн. Это напряжение указывают в процентах к номинальному напряжению первичной обмотки:

U_к%=U_кн/U_1н*100% (4.17)

Полное сопротивление трансформатора при коротком замыкании:

z_к=U_кн/I_1н (4.18)

Активное сопротивление короткого замыкания:

r_к=z_к*cos φ _к (4.19)

Коэффициент трансформации для однофазного трансформатора:

k=E₁/E₂=ω₁/ω₂=U_1н/U_2x, (4.20)

где U_1н – номинальное напряжение первичной обмотки,

U_2x – напряжение вторичной обмотки в режиме холостого хода.

Коэффициент трансформации трехфазного трансформатора зависит от схемы соединения обмоток:

1. при соединении «звезда-звезда» или «треугольник-треугольник»:

k= ω₁/ω₂= E₁/E₂ (4.21)

2. при соединении «звезда-треугольник»:

k¹= *k (4.22)

3. при соединении «треугольник-звезда»:

k¹=k/ (4.23)

Исследование работы трансформатора часто производится на основе векторных диаграмм, построенных для приведенного трансформатора (одной фазы трехфазного), у которого параметры вторичной обмотки приведены к напряжению U_1н и числу витков ω₁ первичной обмотки.

Связь между параметрами вторичной обмотки реального и приведенного трансформаторов:

E¹₂=k*E₂=E₁;

U¹₂=k*U₂;

I¹₂=I₂/k;

r¹₂=k²*r₂;

x¹₂=k²*x₂;

z¹_н=k²*z_н,

где E₂, U₂, I₂, r₂, x₂ – параметры вторичной обмотки реального трансформатора,

z_н – полное фазное сопротивление нагрузки.

Коэффициент полезного действия трансформатора при любой нагрузке определяется по формуле:

η=β*S_н*cos φ ₂/( β*S_н*cos φ ₂+P_x+β²*P_к), (4.24)

где β= I₂/ I_2н – коэффициент нагрузки, определяемый как отношение тока во вторичной обмотке к номинальному току вторичной обмотки,

cos φ ₂ – коэффициент мощности вторичной обмотки.