3. Трехфазные электрические цепи.

3.1 Теоретическая часть.

3.1.1 Понятие о многофазных цепях и системах.

Если между полюсами постоянного магнита (рис. 3.1) вращать в положительном направлении с постоянной скоростью о два жестко скрепленных витка, то в них будут индицироваться ЭДС:

,

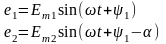вторая из них (е₂) отстает по фазе от первой (е₁) на постоянный угол α.

Определение: Если один источник создает несколько синусоидальных ЭДС, имеющих одну и ту же частоту, но сдвинутых между собой по фазе на некоторые постоянные утлы, то такой источник ЭДС называют многофазным, а совокупность электрических цепей, в которой действует многофазный источник ЭДС - многофазной системой электрических цепей.

О пределение: совокупность синусоидальных токов (напряжений, ЭДС) одной частоты, сдвинутых друг относительно друг друга по фазе, действующих в многофазной системе электрических цепей, называют многофазной системой токов.

Часть многофазной системы электрических цепей, в которой может протекать один из токов многофазной системы, называется фазой. Рис. 3.1

Определение: многофазную систему электрических цепей, в которой отдельные фазы электрически соединены друг с другом, называют многофазной цепью, а многофазную систему электрических токов, в которой отдельные токи равны по амплитуде и отстают по фазе друг относительно друга на утлы 2π/т (т - число фаз) симметричной многофазной системой электрических токов (напряжений, ЭДС).

Многофазные цепи делятся на двухфазные, трехфазные и т.д. Однофазная цепь может быть как частью многофазной цепи, так и самостоятельной цепью.

Из многофазных электрических цепей наибольшее применение нашли трехфазные цепи, предложенные М.О. Доливо-Добровольским в 1891г.

3.1.2 Линейные и фазные величины в трехфазных электрических цепях

Источниками электрической энергии в трехфазных цепях являются трехфазные генераторы, создающие симметричную систему э.д.с:

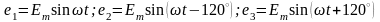, (3.1)

Где начальная фаза е₁, принята равной нулю; векторная диаграмма этих ЭДС показана на рис. 3.2. В данном случае порядок следования фаз является прямым (1, 2, 3); если поменять местами любые два вектора, например, Е_m2 и Е_m2 то порядок следования фаз будет обратным (1; 3, 2, 1; 3, 2, 1…).

Начало и концы первой фазы генератора обозначают большими буквами А и Х соответственно и ее называют фазой А, второй фазы генератора - В и Y и называют фазой В, третьей фазы генератора - С и Z и называют фазой С. Начала и концы фаз потребителя обозначаются малыми буквами а-х, b-у, c-z. Последовательность фаз определяют фазоуказателем, а на распределительных устройствах шины разных фаз имеют различную раскраску: желтый - фаза А, зеленый - фаза В, красный - фаза С.

Комплексные амплитуды ЭДС для (3.1Error: Reference source not found) с учетом обозначения фаз генератора будут:

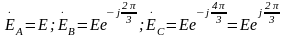. (3.2)

Из (3.1) и (3.2), а также из векторной диаграммы следует:

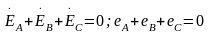(3.3)

120⁰

120⁰

120⁰

Рис. 3.2

Фазы нагрузки трехфазной цепи соединяют звездой (рис. 3.3) или треугольником (рис. 3.4), а фазы генератора, как правило, звездой, так как при соединении этих фаз в треугольник возможно возникновение уравнительных токов в обмотках (фазах) генератора. Эти токи не возникают только тогда, когда суммарная ЭДС фаз генератора равна нулю, что возможно лишь при полной симметрии ЭДС фаз генератора. Для этого нужно выполнить обмотки фаз генератора совершенно одинаковыми, что практически невозможно. Поэтому при соединении фаз генератора в треугольник внутри его возникает отличная от нуля суммарная ЭДС, а так как сопротивления обмоток обычно малы, то даже при небольшой величине суммарной ЭДС в обмотках генератора величина тока будет значительной, они могут перегреваться, срок их службы существенно уменьшается.

Из сказанного видно (рис. 3.3, 3.4), что трехфазный генератор соединяется с нагрузкой четырьмя линейными проводами либо тремя. Общие точки генератора О и потребителя О' называют нулевыми (нейтральными), а провод ОO' - нулевым (О) или нейтральным (N) проводом.

Определение: напряжения между зажимами фаз и нейтральными точками, а также токи в фазах генератора и потребителя называются фазными, а напряжения между линейными проводами и токи в этих проводах называют линейными.

Рис. 3.3

Установим зависимости между линейными и фазными напряжениями и токами в симметричной трехфазной цепи при соединении фаз нагрузки звездой. Из рис. 3.3 видно, что:

I_Ф=I_Л, (3.4)

при этом сумма комплексных токов равна нулю, то есть:

İ_А+İ_В+İ_С=0, (3.5)

поэтому ток в нулевом проводе I₀=0, то есть цепь может быть трехпроводной.

Так как система симметрична, то действующие напряжения порознь фазные и линейные равны:

U_А=U_В=U_С =U_Ф; U_AB=U_BC =U_CA=U_Л; (3.6)

Из векторной диаграммы (рис. 3.4) видно, что:

Рис. 3.4

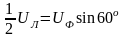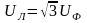или (3.7)

Вывод: в симметричной трехфазной цепи при соединении фаз звездой действующие фазные и линейные токи равны друг другу (3.4), а напряжения отличаются друг от друга в 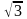раз (3.7).

Благодаря этому в, четырехпроводной трехфазной цепи, возможно дать потребителю два различных напряжения - линейное или фазное. Для цепей низкого напряжения ГОСТом предусмотрены следующие пары напряжений U_Л/U_Ф: 660/380, 380/220 и 220/127 В.

При соединении фаз нагрузки треугольником из рис. 3.4 видно, что:

U_Л=U_Ф (3.8)

и что по первому закону Кирхгофа для узлов а, b, c имеем:

İ_A+İ_ca-İ_ab=0; İ_B+İ_ab-İ_bc=0; İ_C+İ_bc-İ_ca=0, (3.9)

где 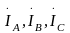- комплексные линейные токи (İ_Л),

İ_ab, İ_bc, İ_ca, - комплексные токи в фазах нагрузки (İ_Ф).

Уравнениям (3.9) отвечает векторная диаграмма на рис. 3.5, из которой видно, что:

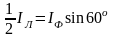или 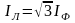(3.10)

Вывод: в симметричной трехфазной цепи при соединении фаз нагрузки треугольником фазные и линейные напряжения равны друг другу (3.8), а линейный ток в раз больше фазного (3.10).

3.1.3 Мощность трехфазной цепи

Активная мощность трехфазной цепи равна сумме активных мощностей фаз:

(3.11)

где U, I - действующие напряжения и ток в фазах;

φ - сдвиг фаз между напряжением и током в фазах.

В симметричной трехфазной цепи

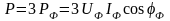(3.12)

При соединении фаз звездой, используя (3.4) и (3.7), получим:

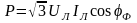(3.13)

а при соединении фаз нагрузки Треугольником, пользуясь (3.8) и (3.10), получаем такое же выражение (3.13) активной мощности.

Реактивная мощность трехфазной цепи по аналогии с (3.11) запишется:

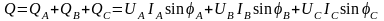
В симметричной трехфазной цепи суммарная реактивная мощность равна утроенной реактивной мощности одной фазы:

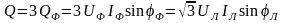(3.14)

Полная мощность трехфазной цепи определяется выражением:

(3.15)

Мгновенная мощность трехфазной цепи равна сумме мгновенных мощностей фаз; в симметричной трехфазной цепи она постоянна, равна активной мощности, а сама цепь

н азывается уравновешенной.

Рис. 3.5

Наиболее простым является расчет симметричный трехфазной цепи при соединении фаз источника и нагрузки звездой (рис. 3.3): потенциалы нулевых точек О и О' равны между собой, поэтому сопротивлением нейтрального провода можно пренебречь, а каждую из фаз можно представить однофазной электрической цепью (рис. 3.6). Обычно задаются ЭДС фазного источника Е, его внутренним сопротивлением Z_ВН , сопротивлением линейного провода Z_L и нагрузки Z_Н , а определяются ток İ и напряжения на отдельных участках:

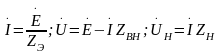(3.16)

где Z_Э=Z_ВН+Z_Н+Z_Л.

Рис. 3.6

Если в симметричной трехфазной цепи фазы нагрузки соединены треугольником, то при расчете целесообразно сначала преобразовать треугольник сопротивлений в звезду, а затем произвести расчет.

При расчёте несимметричных трехфазных цепей следует использовать общие методы: уравнений Кирхгофа, контурных токов и др.