42

1. Цепи постоянного тока.

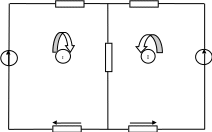
Задача1. Для разветвлённой цепи электрической цепи, пользуясь законами Кирхгофа, определить токи во всех ветвях.

R₄ Б R₃

I₄ I₃

I_I I_II

E₁; R′₀ I₅ R₅ E₂; R″₀

I₁ I₂

R₁ А R₂

Рис. 1.1

1.1 Первый метод расчета

1. Задаёмся произвольным направлением токов.

2. Для узла А: по первому закону Кирхгофа - число уравнений для узла А (*А) равно числу узлов без единицы

∑I_*А = 0; I₅ - I₁ - I₂ = 0. (1)

3. Недостающие уравнения составляем по второму закону Кирхгофа (выбираем контуры с меньшим числом ЭДС и сопротивлений; указываем произвольно направление обхода контура).

4. Значение ЭДС записываем в левой части уравнений. Положительным, если их направления совпадают с направлением обходом контура. Если нет – отрицательным.

5. Аналогично, падение напряжения на участках записывается положительным в правой части уравнения, если направление тока данного участка совпадает с направлением обхода контура.

E₁ = I₁R₁ + I₁R′₀ + I₁R₄ + I₅R₅; (2)

E₂ = I₂R₂ + I₂R″₀ + I₂R₃ + I₅R₅; (3)

Все уравнения (1), (2), (3) решаются совместно и определяются токи на участках цепи.

6. I₅ = I₁ + I₂; (1)

E₁ = I₁ (R₁ + R′₀ + R₄) + I₅R₅; (2)

E₂ = I₂ (R₂ + R″₀ + R₃) + I₅R₅; (3)

7. Подставляем цифровые значения по варианту задания.

E₁ = 80 В

E₂ = 95 В

R′₀ = 0,18 Ом

R″₀ = 0,3 Ом

R₁ = 10 Ом

R₂ = 9 Ом

R₃ = 45 Ом

R₄ = 20 Ом

R₅ = 10 Ом

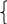
80 = I₁ (10 + 0,18 + 20) + I₅•10;

95 = I₂ (9 + 0,3 + 45) + I₅•10;

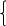
80 = 30,18I₁ + 10I₅;

95 = 54,3I₂ + 10I₅;

80 = 30,18I₁+10I₁ + 10I₂ = 40,18I₁+10I₂;

95 = 54,4I₂ + 10I₁+10I₂ = 64,3I₂ + 10I₁;

10I₁ = 95 – 64,3I₂;

I₁ = 9,5 – 6,43I₂.

80 = 40,18 (9,5 – 6,43I₂) + 10I₂ = 381,71 – 258,36I₂ + 10I₂;

248,36I₂ = 301,71;

I₂= 301,71꞉248,36=1,21 [А]

I₁ = 9,5– 6,43•1,21 = 1,72 [A]

I₅ = 1,72 + 1,21 = 2,93 [A].

Ответ. I₁ = 1,72 [A]

I₂ = 1,21 [A]

I₃ = I₂ = 1,21 [A]

I₄ = I₁ = 1,72 [A]

I₅ = 2,93 [A].

Проверка решения задачи.

Для узла Б: I₄ + I₃ = I₅

1,72 + 1,21 = 2,93 [A]

II метод Метод контурных токов

Основан на применении второго закона Кирхгофа.

1. Сложная электрическая цепь разбивается на элементарные контуры и каждому контуру присваивается свой контурный ток и обозначаются произвольно их направления (I_I, I_II).

2. На участках двух смежных контуров протекают 2 тока: Ток I_I по R₅ и I_II по R₅. Результирующий ток определится как их сумма при согласном направлении и как разность при встречном направлении.

3. Для каждого контура составляют уравнения по второму закону Кирхгофа и, решая их совместно, определяют контурные токи, а затем и действительные их значения на участках цепи.

Для первого контура:

I E₁ = I_IR₁ + I_IR′₀ + I_IR₄ + I_IR₅ + I_IIR₅ = I_I (R₁ + R′₀ + R₄ + R₅) + I_IIR₅;

Для второго контура:

II E₂ = I_IIR₂ + I_IIR″₀ + I_IIR₃ + I_IIR₅ + I_IR₅ = I_II (R₂ + R″₀ + R₃ + R₅) + I_IR₅;

80 = I_I (10 + 0,18 + 20 + 10) + I_II•10;

80 = 40,18I_I + 10I_II;

95 = I_II (9 + 0,3 + 45 + 10) + I_I•10;

95 = 64,3I_II + 10I_I → 10I_I = 95 – 64,3I_II;

I_I = 9,5 – 6,43I_II;

80 = 40,18 (9,5 – 6,43I_II) + 10I_II;

80 = 381,71– 258,36I_II + 10I_II;

248,36I_II = 301,71;

I_II = 301,71꞉248,36 = 1,21 [A].

I_I = 9,5 – 6,43•1,21 = 1,72[A]

I₁ = I_I = I₄ = 1,72 [A]

I₅ = I_I + I_II = 1,72+1,21=2,93[A]

I₂ = I_II = I₃ = 1,21 [A]