МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. Н.Э. БАУМАНА

Я. В. Мыкольников, А. В. Пельтин

Методические указания к лабораторной работе

«Исследование основных характеристик навигационной аппаратуры потребителя»

по курсу

«радионавигационные системы»

Под редакцией И. Б. Власова

Москва

МГТУ им. Н.Э. Баумана

2009

Исследование особенностей работы навигационной аппаратуры потребителя

глобальных навигационных спутниковых систем

Цель работы – ознакомление с режимами и условиями работы навигационной аппаратуры потребителя (НАП).

На данной лабораторной установке выполняются следующие работы:

1. Исследование зависимости точности навигационных определений от состава и геометрии рабочего созвездия навигационных космических аппаратов (НКА).

2. Исследование надежности работы навигационной аппаратуры потребителя (НАП) в условиях постановки помех.

Работа №1. Исследование зависимости точности навигационных определений от состава и геометрии рабочего созвездия НКА.

Теоретическая часть

Для решения задачи непрерывной глобальной всепогодной и одномоментной навигации неограниченного количества потребителей созданы ГНСС ГЛОНАСС (РФ) и GPS (США), в которых реализован метод пассивных (беззапросных) псевдодальномерных и пседодоплеровских измерений по сигналам нескольких НКА [1,2].

В штатном составе орбитальная группировка НКА обеих систем включает 24 НКА, которые упорядоченно движутся по круговым средневысотным орбитам (порядка 20 тыс. км) и синхронно излучают навигационные радиосигналы.

Основным содержанием навигационной задачи является определение пространственных координат потребителя, составляющих вектора его скорости, а также текущего времени [3]. Поэтому в результате решения навигационной задачи должен быть определен расширенный вектор состояния потребителя П, который в инерциальной геоцентрической системе координат OXYZ можно представить в виде , где x, y, z – координаты потребителя; V_x, V_y, V_z – составляющие вектора скорости потребителя; t – текущее время (в той или иной временной шкале).

Элементы вектора состояния П недоступны непосредственному измерению с помощью радиосредств. У принятого радиосигнала могут измеряться те или иные его параметры, например задержка или доплеровское смещение несущей частоты. Измеряемый в интересах навигации параметр радиосигнала называют радионавигационным (РНП), а соответствующий ему геометрический параметр – навигационным (НП). Поэтому задержка распространения сигнала  и доплеровское смещение частоты F_д являются РНП, а соответствующие им дальность R от источника до приемника и радиальная скорость сближения объектов V_r служат НП, связь между которыми дается следующими соотношениями:

; ,

где с – скорость света;  - длина волны излучаемого радиосигнала.

Геометрическое место точек пространства с одинаковым значением навигационного параметра называют поверхностью положения [4].

Наиболее простой метод беззапросных навигационных определений – дальномерный, который основан на измерениях дальности R_i между i-м НКА и потребителем. Соответственно, навигационным параметром является дальность R_i, а поверхностью положения — сфера радиуса R_i, центр которой расположен в центре масс i-го НКА. Уравнение этой сферы имеет вид:

, (1)

где - номер НКА.

Здесь - известные на момент измерения координаты i-го НКА (с учетом его перемещения за время распространения сигнала); - координаты потребителя.

Координаты потребителя, определяют как координаты точки пересечения трех поверхностей положения (трех сфер). Поэтому для реализации дальномерного метода необходимо измерить дальности до трех НКА, т. е. i = 1...3 (см. рис. 1).

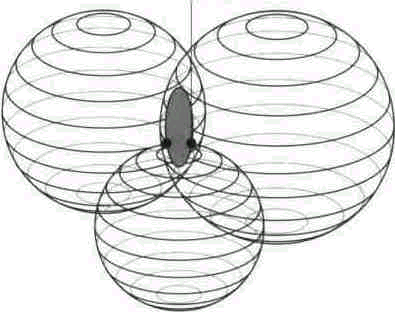
Рис. 1 – Иллюстрация дальномерного метода измерения

Таким образом, для дальномерного метода навигационная функция представляет собой систему из трех квадратных уравнений вида (1). Ввиду нелинейности такой системы уравнений возникает проблема неоднозначности определения координат потребителя, устраняемая с помощью известной потребителю дополнительной информации (априорные координаты потребителя, его радиальная скорость и т. д.).

В (1) неявно подразумевается, что все входящие в это выражение величины относятся к одному и тому же моменту времени. Однако координаты НКА привязаны к бортовой шкале времени (БШВ), а потребитель измеряет задержку сигнала и определяет свои координаты в своей шкале времени (ШВ). Если БШВ НКА и ШВ потребителя идеально синхронизированы, то проблем не возникает. При наличии расхождения шкал времени возникает смещение измеренной дальности относительно истинной и точность определения местоположения потребителя падает, поэтому недостатком метода является необходимость очень точной привязки шкал времени НКА и потребителя.

Уменьшить влияние этого фактора можно, установив у потребителя высокостабильный эталон времени (частоты) и периодически проводя его калибровку по ШВ НКА. Однако применение в НАП дорогостоящих высокостабильных эталонов времени экономически не оправдано, а проблема создания относительно дешевых высокостабильных эталонов времени (частоты) в настоящее время не решена. Поэтому в настоящее время более широко применяют псевдодальномерный метод.

Под псевдодальностью от i-го НКА до потребителя понимают измеренную дальность этого НКА, отличающуюся от истинной дальности Ri на неизвестную, но постоянную за время определения навигационных параметров величину . Таким образом, для псевдодальности до i-го НКА можно записать

, (2)

где – смещение временной шкалы потребителя относительно системного времени.

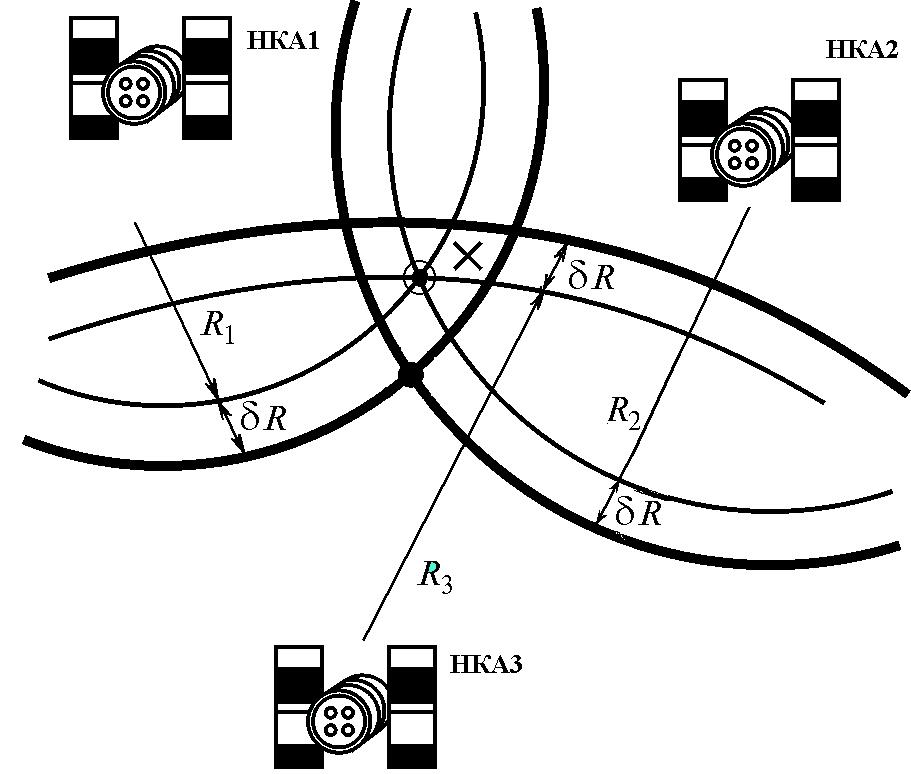
Рис. 2 - Иллюстрация псевдодальномерного метода измерения

В псевдодальномерных методах в качестве навигационного параметра выступает псевдодальность . Поверхностью положения по-прежнему является сфера с центром в точке центра масс НКА, но радиус этой сферы отличается от истинной дальности R на неизвестную величину . Шкалы времени НКА синхронизированы с высокой точностью, величина задержки считается одинаковой для всех НКА (рис. 2).

Измерение псевдодальностей до трех НКА приводит к системе трех уравнений, содержащих четыре неизвестных – координаты потребителя и задержку . Для устранения возникшей неопределенности необходимо провести дополнительное измерение, т. е. измерить псевдодальность до четвертого спутника. Именно необходимость нахождения в зоне видимости четырех НКА в значительной степени определяет структуру и параметры орбитальной группировки НКА.

Псевдодальномерный метод не накладывает жестких ограничений на значение погрешности временной шкалы потребителя, поскольку позволяет одновременно с определением местоположения вычислять вычислить эту погрешность и, при необходимости, скорректировать ее.

Однако и формула (2) также является идеализированным выражением для формируемого в НАП отсчета псевдодальности, т.к. не учитывает расхождение БШВ отдельных НКА от ШВ системы, задержки радиосигнала на трассе распространения, а также аппаратурные ошибки в приемном устройстве. В самом общем виде формируемый навигационным приемником отчет псевдодальности можно описать следующей моделью измерений:

, (3)

где	S	- измерение псевдодальности;
	R	- дальность от НКА до приемника, - координаты НКА на мо­мент излучения, - координаты НАП на момент приема сигнала;
		- ошибка эфемеридного обеспечения;
		- расхождение шкалы времени приемника с системной шкалой времени;
		- расхождение шкалы времени НКА с системной шкалой времени;
		- задержка сигнала в тропосфере;
		- задержка сигнала в ионосфере;
		- аппаратурная задержка сигнала в приемнике;
		- ошибка, обусловленная приемом переотраженных сигналов (многолучевостью);
		- аппаратурная ошибка измерения;
	с	- скорость света в вакууме.

Погрешности, возникающие на трассе распространения, в основном обусловлены рефракцией сигналов в атмосфере (тропосфере и ионосфере) Земли.

Ионосферная рефракция сигнала НКА, вызванная различиями диэлектрической проницаемости слоев, расположенных на разных высотах, а также локальными неоднородностями, изменяется в широких пределах в зависимости от района Земли, где расположена НАП, времени суток, года, солнечной и геомагнитной активности и т. д., и составляет 5...500 нс, что эквивалентно ошибке измерения псевдодальности в 1,5 … 150 м.

Среднее значение этой погрешности для углов возвышения близких к 90⁰ составляет в ночное время 5...10 нс и 30...50 нс – в дневное. При углах возвышения порядка 15⁰ эти величины возрастают в 2...3 раза. Таким образом, учитывать эти погрешности необходимо только в случаях, когда суммарная погрешность навигационных определений не должна превышать 5…10 м.

Поскольку ионосфера, в отличие от тропосферы, является диспергирующей средой, то для оценки задержки сигнала в ней может быть использован метод двухчастотных измерений, обеспечивающий остаточную погрешность порядка 1…2 м. Именно поэтому НКА последних поколений излучают навигационные сигналы в двух частотных диапазонах L1 (1,6 ГГц) и L2 (1,25 ГГц). Кроме того, для определения и учета ионосферной погрешности в НАП в настоящее время применяются метод моделирования условий на трассе распространения сигналов НКА и метод избыточных одночастотных измерений.

Основная составляющая тропосферной погрешности навигационных определений в ГНСС обусловлена тропосферной рефракцией, связанной с неоднородностями диэлектрической проницаемости. Дополнительная задержка сигнала НКА в тропосфере может достигать 8...80 нс (экспериментальные данные для ГНСС GPS), что может приводить к ошибке измерения. Поскольку в диапазоне L1 величина задержки в тропосфере не зависит от частоты (дисперсия сигнала отсутствует), измерить эту задержку с помощью двухчастотного сигнала невозможно.

Значение тропосферной рефракции, пропорциональное длине пути сигнала в тропосфере, максимально при малых углах возвышения НКА над горизонтом. Поэтому для уменьшения атмосферных погрешностей в НАП измерения производятся только тех НКА, угол возвышения которых превышает некоторое значение ("угол маски"), устанавливаемое потребителем. Обычно этот угол составляет 5...10°.

Многолучевость распространения сигналов НКА в точке расположения антенны НАП имеет своей причиной их переотражение от земной и морской поверхностей и близлежащих объектов. Уровень отраженного сигнала может быть соизмеримым с прямым сигналом, а его задержка относительно прямого сигнала для НКА, находящегося в зените, может составлять от единиц до сотен мкс (при расположении НАП на борту самолета); при небольших углах возвышения НКА это значение уменьшается на порядок. Многолучевость приводит к существенным искажениям полезного сигнала и к погрешностям в схемах слежения за задержкой, частотой и фазой.

С этой точки зрения в ГНСС предпочтительно использовать модулирующие дальномерные псевдослучайные последовательности (ПСП) с максимальной базой, например, Р(Y)-код GPS или ВТ-код ГЛОНАСС. Их применение позволяет снизить погрешности из-за многолучевости в среднем до 1...3 м (СКО). При использовании в условиях многолучевости более узкополосных сигналов стандартной точности (С/А GPS или СТ ГЛОНАСС) применяются специальные методы коррекции импульсной характеристики коррелятора, позволяющие снизить вероятность захвата схемами слежения пиков взаимной корреляционной функции ,обусловленных приемом отраженных сигналов.

Источниками аппаратурных ошибок измерения псевдодальности являются в основном схемы слежения за задержкой огибающей и несущей (ЧАП и ФАП) сигналов НКА. Среднеквадратическое отклонение (СКО) шумовой погрешности типовой некогерентной схемы слежения за огибающей описывается следующим выражением:

, (4)

где - длительность элемента кода ПСП; - постоянные коэффициенты, зависящие от выбранной схемы слежения; - односторонняя ширина полосы замкнутой схемы слежения и тракта промежуточной частоты соответственно; - отношение мощности сигнала к спектральной плотности шума приведенная ко входу НАП.

За счет специальных мер можно снизить флуктуационную составляющую ошибки измерения псевдодальности до 0,2 м для СТ-кода ГЛОНАСС и до 0,1 м для С/А кода GPS.

При использовании в НАП шаге квантования, равном 1/64 , соответствующие погрешности измеряемой дальности составляют 0,27 м для P-кода и 2,66 м для C/A-кода GPS.

Динамическую составляющую дальномерной погрешности АП можно оценить как , где - скорость изменения доплеровского сдвига частоты. Это соотношение справедливо для установившегося режима схемы слежения второго порядка при квадратичном законе изменения задержки сигнала. Типовые значения этой погрешности составляют порядка 1,2 мм для C/A-кода GPS.

Погрешности, связанные с функционированием бортовой аппаратуры НКА и наземного комплекса управления (НКУ) ГНСС обусловлены в основном несовершенством частотно-временного и эфемеридного обеспечения.

Погрешности частотно-временного обеспечения возникают вследствие несовершенства аппаратуры бортового эталона, а также процедур сверки бортовой ШВ с системным эталоном. Они проявляются, например, в смещении фаз излучаемых дальномерных кодов и меток времени, что приводит к погрешностям измерения расстояния до спутника и расчета его координат.

По результатам многолетних наблюдений СКО сдвига бортовой ШВ через 2 часа после коррекции составляет примерно 9 нс, а через сутки после коррекции он достигает 25,4 нс для цезиевых и 108 нс для рубидиевых эталонов. На НКА ГЛОНАСС устанавливается цезиевый эталон, а на НКА GPS – комбинированный цезиево-рубидиевый.

Погрешности эфемеридного обеспечения вызваны неточностью расчета параметров орбит НКА в НКУ и непрогнозируемыми отклонениями реальной орбиты НКА относительно экстраполированной. Составляющие вектора этой погрешности: продольная, поперечная и радиальная - имеют величины порядка 0,6...10 м . Эфемеридная компонента представляет собой проекцию указанного вектора на линию визирования НКА. При этом имеющие максимальную величину продольная и поперечная составляющие входят в суммарную погрешность с коэффициентом, обычно не превышающим 0,25, а радиальная составляющая, лежащая в пределах 0,6…2 м практически полностью входит в дальномерную погрешность. Для системы GPS, по данным литературы, эфемеридная погрешность равна примерно 1 м (СКО). Общий бюджет погрешностей измерения НП приведен в таблице 1.

Таблица 1 Бюджет погрешностей определения псевдодальности

Источник ошибки	ГЛОНАСС	GPS
Погрешность частотно-временного обеспечения	2	1.1
Задержка сигнала в ионосфере	4	0.1
Задержка сигнала в тропосфере	0.5	0.2
Многолучевость	2.5	0.2
Аппаратурные погрешности приемного устройства	1.5	0.1
Прочие	2	0.8
Суммарная погрешность	5.7	1.4

В соответствии с (3) искомые нами координаты потребителя связаны с НП нелинейной зависимостью. Одним из методов решения системы уравнений вида (3) является линеаризация уравнения путем разложения нелинейной части уравнения в ряд Тейлора с удержанием первых членов разложения

(5)

Применяя (5) к (3) получим следующее выражение:

, (6)

Для оценивания 4‑х неизвестных: и необходимо одновременно измерить псевдодальности по 4‑м. При наличии более 4‑х измерений, т.е. их избыточности, точность оценивания неизвестных будет расти. При решении навигационной задачи по сигналам двух систем необходимо учитывать, что каждая ГНСС имеет собственную системную ШВ, поэтому в число неизвестных будет также входить разность между системными ШВ, а общее количество неизвестных возрастет до 5, как и минимальное количество измерений.

Систему уравнений вида (6) можно в общем виде записать следующим образом:

(7)

где – градиентная матрица размерностью . Строки матрицы состоят из транспонированных векторов типа и величины (четвёртый элемент строки).

В этом случае максимально правдоподобная оценка вектора выражается хорошо известной формулой [5]:

. (8)

Получаемая оценка содержит ошибку линеаризации дальности относительно вектора . Ошибка считается допустимой, если

, (9)

где – дальность относительно .

Иначе производится новый этап линеаризации относительно для формирования новой оценки вектора .

Практика обработки измерений показывает, что обычно достаточно 4‑х последовательных этапов, чтобы получить оценку этого вектора, для которой ошибкой линеаризации можно пренебречь.

При фиксированных значениях погрешностей измерения псевдодальностей существенное влияние на точность местоопределения оказывает взаимное положение НАП и рабочих НКА, которое определяет углы пересечения поверхностей положения. Минимальным погрешностям местоопределения для дальномерных методов соответствует такое расположение НКА, при котором в точке расположения АП поверхности положения пересекаются под прямым углом (рис. 3). Однако выполнить это условие при одновременном наблюдении более трех НКА невозможно.

Рис. 3 – Влияние геометрии созвездия на точность НВО

Количественной характеристикой погрешности местоопределения, связанной с особенностями пространственного положения НКА и АП, служит т.н. геометрический фактор или коэффициент геометрии. В иностранной англоязычной литературе используется обозначение GDOP (Geometrical delusion of precision – геометрический фактор ухудшения точности).

Для того чтобы уточнить математический смысл понятия геометрического фактора, запишем зависимость вектора погрешности, определяемых с помощью (8) параметров g, от вектора погрешности измеряемых НП

(10)

С учетом (10) получим корреляционную матрицу ошибок навигационных определений потребителя в виде

(11)

где - корреляционная матрица погрешностей измерения НП (псевдодальностей); - соответственно векторы математических ожиданий погрешностей .

Примем равными нулю составляющие вектора . Тогда = 0 и дисперсии определяемых параметров , т.е. диагональные члены матрицы , полностью определяют погрешности навигационного сеанса. Анализ выражения (11) показывает, что соотношение погрешностей определения вектора потребителя и измеряемых НП зависит только от вида матрицы градиентов , т.е. от геометрии взаимного положения НКА и НАП.

Как правило, вводится для случая, когда погрешности измерения НП, т.е. элементы матрицы , равновелики и некоррелированы. В этом случае (11) можно представить в виде

. (12)

Тогда выразив дисперсию сеанса навигационных определений через след матрицы .

, (13)

можно представить геометрический фактор в виде коэффициента

. (14)

При выборе орбитальных параметров НКА на этапе разработки СРНС, а также при выборе рабочего созвездия НКА в малоканальной аппаратуре является основным критерием.

Иногда удобно рассматривать по отдельности значения геометрических факторов, характеризующих точность определения различных компонент вектора состояния. Соответствующий геометрический фактор для пространственных координат обозначают (в иностранной англоязычной литературе используют обозначение PDOP – Position DOP), для плановых (горизонтальных) координат - (англ. HDOP – Horizontal DOP), для высоты (вертикальной составляющей) - (англ. VDOP – Vertical DOP), для временного параметра - .(англ. TDOP – Time DOP). Между этими коэффициентами и суммарным геометрическим факторам существует простая связь

. (15)

Показано, что минимальное значение достигается в случае, когда потребитель находится в центре правильного тетраэдра. Соответственно для наземного потребителя, с учетом кривизны земной поверхности, минимальное значение достигается тогда, когда один НКА находится в зените, а три других равномерно расположены в горизонтальной плоскости, т.е. когда объем тетраэдра максимален.

Однако такая геометрия рабочего созвездия, как уже говорилось, не оптимальна с точки зрения атмосферных ошибок, поэтому при используемых на практике углах возвышения (углах маски) более 10⁰ минимальное значение _.

Работа №2. Исследование надежности работы навигационной аппаратуры потребителя (НАП) в условиях постановки помех.

Теоретическая часть

Характерной особенностью такой внутрисистемной помехи является то, что на приемной стороне известна внутренняя структура помехового сигнала. Помехи такого рода получили название структурно-детерминированных [5]. Использование знания внутренней структуры сигнала помехи перспективно с точки зрения повышения помехоустойчивости алгоритмов обработки сигналов.

Проблеме повышения помехоустойчивости навигационной аппаратуры в настоящее время уделяется большое внимание. Известные алгоритмы первичной обработки навигационных сигналов, позволяющих получить повышенную помехоустойчивость, приведены ниже.

Повысить помехоустойчивость НАП возможно при помощи комплексирования следящих систем с другими вспомогательными источниками информации. Повышение помехоустойчивости достигается за счет сужения шумовых полос следящих систем. В качестве вспомогательного источника информации может быть использован сигнал от систем ФАПЧ, сопровождающих другие НКА (т.н. алгоритм Co-Op Tracking), сигнал от доплеровских измерителей скорости, а также сигнал от инерциального датчика. Данные алгоритмы комплексирования позволяют повысить помехоустойчивость следящих систем на 2…10дБ.

Другим направлением создания помехоустойчивых алгоритмов первичной обработки сигналов является адаптивная фильтрация сигнала перед первичной обработкой. В таких алгоритмах используется перестраиваемый режекторный фильтр, выполняющий функции обеления помехи.

При помощи режекторного фильтра возможно достичь высоких показателей подавления узкополосных помех. В частности, при ширине полосы помехи до 10Гц алгоритм обеспечивает работу навигационного приемника при отношениях помеха/сигнал более 70дБ. Однако общим недостатком таких алгоритмов является то, что эффективность помехоподавления уменьшается при увеличении полосы частот помехи (за счет вырезания вместе с помехой части полезного сигнала). Кроме этого в рассматриваемых навигационных комплексах структура сигнала, образующего внутрисистемную помеху, подобна структуре полезного сигнала НКА. Типовой является ситуация, когда спектр сигнала и спектр помехи совпадают. В таких условиях использование обеляющего фильтра не представляется возможным.

Наиболее перспективными являются алгоритмы компенсации помехи, подразумевающие оценивание параметров, как полезного сигнала, так и помехи, а также вычитание из входного сигнала восстановленной помехи. В отличие от метода использования обеляющего фильтра алгоритм компенсации помехи использует знание структуры помехового сигнала, поэтому последний при одинаковых условиях обеспечивает более эффективное помехоподавление. Эффективность алгоритма компенсации при этом не зависит от ширины полосы помехи.

Применительно к задаче приема навигационных сигналов в НАП, работающей при наличии внутрисистемной структурно-детерминированной помехи, алгоритм, синтезированный в, имеет ограниченное применение. Следует заметить, что наличие информационной модуляции в помеховом сигнале является существенным фактором, ограничивающим применение компенсационных алгоритмов на практике.

Стремление обеспечить помехоустойчивый прием при наличии информационной модуляции в помеховом сигнале привело к появлению алгоритмов основанных на частичной корреляции в приемнике. Суть данного алгоритма заключается в том, что в качестве опорного сигнала в корреляционном приемнике используется ПСП не в точности совпадающая с полезным сигналом, а измененная. Измененная ПСП должна удовлетворять следующим двум условиям: отсчет взаимной корреляционной функции ее с помеховой ПСП должен быть нулевым, уменьшение отсчета корреляционной функции с ПСП полезного сигнала должно быть минимально приводится алгоритм синтеза такой ПСП, а предлагается упрощенный вариант алгоритма. Общей характерной особенностью данного подхода является то, что использование измененной ПСП приводит к уменьшению энергетики полезного сигнала, а кроме того, как отмечают сами авторы метода, сложно подобрать опорную ПСП при наличии доплеровского сдвига частоты между полезным сигналом и помехой.

Анализ литературы показывает, что аналогичная проблема – защита от внутрисистемных помехи, имеется в системах сотовой связи с кодовым разделением каналов (CDMA – Code Division Muliple Access), получившая название проблемы близко-далеко (Near-Far Problem). Предлагалось множество алгоритмов, предназначенных для повышения помехозащищенности приемного устройства в такой ситуации, названных многопользовательскими детекторами (МПД). Основополагающей работой по данному вопросу считается работа, в которой проведен синтез оптимального алгоритма приема сигнала при наличии внутрисистемной межканальной помехи.

Из приведенного обзора видно, что задача синтеза алгоритма оценивания параметров решена строго только для приема сигналов НКА при действии узкополосной помехи, не несущей информационной модуляции. Наличие информационной модуляции в помехе делает невозможным применение известных компенсационных алгоритмов, которые являются наиболее эффективными.

В данной лабораторной работе качественно рассматривается влияние узкополосной помехи на работоспособность НАП, использующей некоторую разновидность алгоритмов компенсации помехи указанного типа.

Экспериментальная часть

1. Краткое описание лабораторного стенда.

В состав лабораторного стенда входят:

1. Преподавательский компьютер.

2. Персональные компьютеры пользователей.

3. ГЛОНАСС / GPS приемник.

4. Активная антенна ГЛОНАСС / GPS.

5. Генератор сигналов Agilent E4420B.

6. Т-Мост Agilent 86205A.

7. Осциллограф Agilent DSO-3202A.

8. Источники питания активной антенны и приемника Agilent E3832A.

9. Сетевой коммутатор Switch D-Link

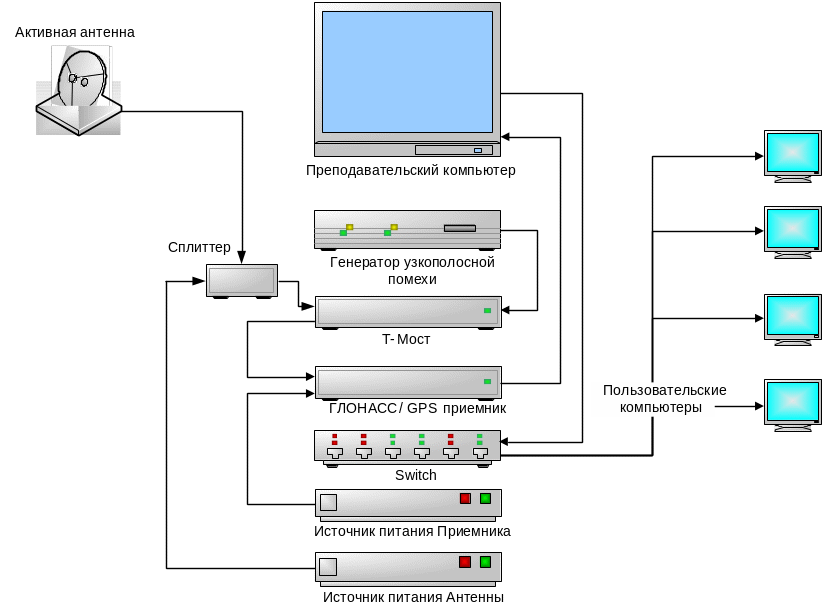
Рис. 4 – Схема лабораторного стенда

Структура лабораторного стенда приведена на рисунке 4. Внешний вид лабораторного стенда приведен на рисунке 5.

Прием и обработку сигналов НКА осуществляет одноплатный комбированный ГЛОНАСС/GPS 20 канальный приемник. Активная приемная антенна установлена на крыше здания для обеспечения приема радиосигналов максимально возможного количества НКА. Управление работой НАП осуществляется с промышленного компьютера, установленного в стойке. Информационный обмен между приемным устройством и компьютером осуществляется в текстовом формате NMEA-0183. Результаты навигационно-временных вычислений передаются на персональные компьютеры студентов через локальную сеть.

Рис. 5 – Внешний вид лабораторного стенда

2. Описание лабораторного навигационного приемника Topcon Half Euro Card

Topcon Javad Half Eurocard GG - одноплатный комбированный L1 GPS/L1 ГЛОНАСС/WAAS приемник - предназначен для вычисления координат, вектора скорости, курса и времени по сигналам спутниковых навигационных систем GPS (США) и ГЛОНАСС (РОССИЯ). Приемник имеет 2 асинхронных последовательных порта типа RS-232 для связи с внешним оборудованием. Приемник может работать как в автономном, так и в дифференциальном режимах. Приемник формирует секундную метку времени (1PPS signal), синхронную с одной из выбранных шкал времени. Внешний вид приемника представлен на рисунке 6.

Topcon Half Eurocard GG Receiver

Рис. 6 – Внешний вид НАП

Технические параметры

• 20 каналов, all-in-view, L1 GPS, WAAS and L1 GLONASS

• Слежение за слабым сигналом (Менее 30 dB*Hz)

• Быстрый поиск и быстрое обновление

• Слежение за спутниками с низким уровнем сигнала

• Возможна установка на высокодинамичные объекты, до 30g

• Нет ограничений по высоте и скорости

Информационные характеристики

• До 20 Гц обновления данных в реальном времени.

• Точность по кодовому разделению 10см и 0.1 мм по фазе сигнала.

• RTCM SC104 versions 2.1 and 2.2 Input/Output

• NMEA 0183 версии 2.1, 2.2, 2.3 и выход 3.0

• Составная база RTCM

• Геоидная и магнитная модели

• RAIM

• Поддержка разных характеристик DATUM

• Вывод координат

• CMR и CMR+ поддержка

Входы и выходы

• 2 высокоскоростных порта (460.8 Kbps) стандарта RS232

• 1 PPS выход (TTL) синхронизированный с GPS, UTC, или GLONASS

• Ввод событийных отметок

Питание

• Питание приемника осуществляется в диапазоне от 4.5 вольт до 14 вольт.

• Встроенный источник питания постоянного тока позволяет хранить информацию в течение 10 лет.

Рабочие диапазоны

• Рабочая температура – 40 ⁰C … + 75 ⁰C

• Температура хранения – 40 ⁰C … + 75 ⁰C