Матрица смежности s (g)

	1	2	3	4	5	6	7	8	9	10
1	0	i	0	0	a	0	0	h	0	0
2	0	0	j	0	0	l	0	n	o	0
3	0	0	0	k	0	0	0	0	0	0
4	0	0	0	0	0	0	0	0	0	e
5	0	0	0	0	0	b	0	0	0	0
6	0	0	m	0	0	0	c	0	0	0
7	0	0	0	d	0	0	0	0	0	0
8	0	0	0	0	0	0	0	0	g	0
9	0	0	p	0	0	0	0	0	0	f
10	0	0	q	0	0	0	0	0	0	0

Граф называется сильно связным, если любая пара вершин соединена путем /1/.

Максимальный по включению вершин сильно связный подграф графа называется его компонентой сильной связности. Граф называется несильно связным, если число его компонент сильной связности больше 1.

Теперь мы можем воспользоваться теоремой, которая говорит, что граф состоит из k компонент связности тогда и только тогда, когда его матрица достижимости является k-клеточной.

Матрица А называется k- клеточной, если в результате перестановки строк и столбцов она приводится к виду, показанному в табл. 3.8, где подматрица А , i = 1, …. k, не содержит ни одного нулевого элемента (кроме, быть может, диагональных).

Таблица 3.8

А	0	0	…	0
0	А	0	…	0
0	0	А	…	0
…	…	…	…	…
0	0	0	…	А

Максимальная степень, в которую необходимо возвести матрицу смежности, равна диаметру графа. Его можно определить так:

d(G)=max min l (v_i ,v_j), где l-длина дуги от v_i до v_j вершины.

j i

Диаметр нашего графа оказался равен 4. Найдем матрицу достижимости по формуле:

D(G)=

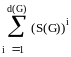
где S(G)-матрица смежности;

i=1…d(G);

d(G)-диаметр графа;

Для нашего графа S² (G)+ S³ (G)+ S⁴ (G)

Составим матрицы S² (G) (табл. 3.9), S³ (G) (табл. 3.10), S⁴ (G) (табл. 3.11).

При возведении в n-ю степень матрицы смежности S= умножение рассматриваем как конкатенацию – приписывание справа к идентификатору, соответствующему i-ой строке, идентификатора, соответствующего j – му столбцу, суммирование – как объединение полученных в результате умножения слов.

Таблица3.9