Решение.

У руководства магазина А имеется четыре стратегии Аi : продавать товар i –го вида (i=1...4), аналогично у руководства магазина В есть 4 стратегии Вj- продавать товар j-го вида (j=1...4).

Запишем платежную матрицу

	b1	b2	b3	b4	min
a1	-23	62	62	62	-23
a2	57	-32	57	57	-32
a3	43	43	-31	43	-31
a4	65	65	65	-34	-34
max	65	65	65	62

Определим имеет ли игра оптимальное решение в чистых стратегиях

α=maxmin aij

β=minmax aij

α= -23 β=62

Так как α≠β, то игра не имеет решения в чистых стратегиях.

Для того чтобы свести игру к паре двойственных задач линейного программирования увеличим все элементы на 34

	b1	b2	b3	b4
a1	11	96	96	96
a2	91	2	91	91
a3	77	77	3	77
a4	99	99	99	0

Запишем задачу линейного программирования для игрока А

f=y1+y2+y3+y4(min)

11у1+91у2+77у3+99у4≥1

96у1++2у2+77у3+99у4≥1

96у1+91,3у2+3у3+99у4≥1

96у1+91у2+77у3≥1

уi≥0

Решим задачу с помощью модуля ПОИСК РЕШЕНИЯ

	b1	b2	b3	b4		переменные	вероятности
a1	11	96	96	96	у1	0,003685	0,252376
a2	91	2	91	91	у2	0,00352	0,241033
a3	77	77	3	77	у3	0,004233	0,289891
a4	99	99	99	0	у4	0,003164	0,216686
	1	1	1	1		0,014602	68,48376	цена игры
	1	1	1	1

Оптимальная стратегия магазина А: продажа 25,24% товара 1, 24,10% товара 2, 28,99% товара 3 и 21,67% товара 4, Zmin = Z´max = 0,014602 ν = 1/0,014602=68,48376

		Результ.	Нормир.	Целевой	Допустимое	Допустимое
Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
$G$2	у1 переменные	0,003685195	0	1	0,621728435	0,438186034
$G$3	у2 переменные	0,003519568	0	1	0,483677718	0,458806553
$G$4	у3 переменные	0,004232994	0	1	0,184463965	0,853486383
$G$5	у4 переменные	0,003164056	0	1	0,64881561	0,510357851
		Результ.	Теневая	Ограничение	Допустимое	Допустимое
Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
$B$6	b1	1	0,004726755	1	0,484728049	0,885416667
$C$6	b2	1	0,00369399	1	0,460839622	0,978021978
$D$6	b3	1	0,001680266	1	0,464709134	0,961038961
$E$6	b4	1	0,004500804	1	0,456116108	1

Запишем задачу линейного программирования для игрока В

f=x1+x2+x3+x4(max)

11х1+96x2+96x3+96x4≤1

91x1+2x2+91х3+91x4≤1

77x1+77x2+3x3+77x4≤1

99x1+99x2+99x3≤1

xi≥0

Магазин В:

использует стратегию B1 на 32,35 %((0,004726755*68,43766)*100%=32,35%)

использует стратегию B2 на 25,29 %

использует стратегию B3 на 11,50 %

использует стратегию B4 на 30,86 %

Вывод. Определены оптимальные стратегии магазинов. Оптимальная стратегия магазина А: продажа 25,24% товара 1, 24,10% товара 2, 28,99% товара 3 и 21,67% товара 4, Zmin = Z´max = 0,014602 ν = 1/0,014602=68,48376

Магазин В:

использует стратегию B1 на 32,35 %

использует стратегию B2 на 25,29 %

использует стратегию B3 на 11,50 %

использует стратегию B4 на 30,86 %

Задача 19

=7920 s =12 k=210 Ө=30

Решение.

Оптимальный размер партии

Интервал поставки τ(опт)=q(опт)*365/

Годовые издержки

Точка заказа

r(опт)=*Ө= (Ө/τ)*q

Минимальный начальный запас

I0=Ө

Размер поставки	q	527	Ед
Интервал между поставками	τ(опт)	24,3	Дней
Годовые издержки	L(опт)	6318	Д.е./год
Точка заказа	r(опт)	650,9	Ед
Минимальный начальный запас	I0	650,9	Ед

При поставках один раз в месяц годовые издержки составят 6480 д.е.год (при этом объем партии 660 единиц), поэтому оптимизация поставок позволяет сэкономить 162 ден.ед.

Построение графика.

Время	текущий запас	фиксированный запас	точка заказа
0	650,9	1177,9	650,9
24,3	123,9	650,9	650,9
24,3	650,9	1177,9	650,9
48,6	123,9	650,9	650,9
48,6	650,9	1177,9	650,9
72,9	123,9	650,9	650,9
72,9	650,9	1177,9	650,9

График текущего и фиксированного состава

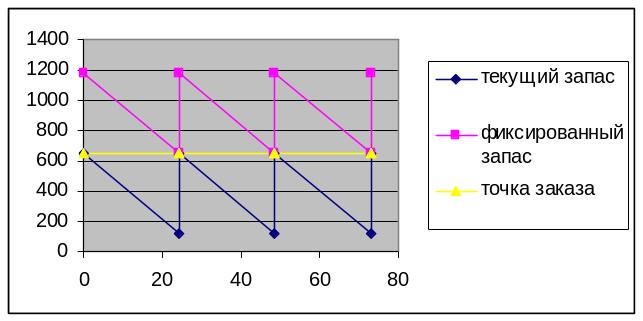
Вывод. Оптимальный объем партии составляет 527 единиц, точка заказа -650,9 ед, оптимизация поставок позволяет уменьшить затраты на 162 ден.ед. (по сравнению с поставками раз в месяц).