
Контрольная работа.
Задача 1.
По данным 16 предприятий постройте модель парной линейной регрессии зависимости затрат на производство (млн.д.е.) от объема выпуска продукции (тыс.ед.). Оцените качество и рассчитайте прогноз затрат на производство, если объем выпуска составит 120% от его среднего уровня
Таблица.
№п/п |
Объем выпуска, тыс.ед. |
Затраты на производство, млн.ден.ед. |
i |
х |
у |
1 |
3,5 |
34,1 |
2 |
4,1 |
29,3 |
3 |
7,6 |
11,5 |
4 |
5,2 |
27,6 |
5 |
4,9 |
27,0 |
6 |
12,7 |
8,9 |
7 |
14,9 |
8,6 |
8 |
10,7 |
6,8 |
9 |
9,5 |
4,0 |
10 |
9,4 |
9,2 |
11 |
4,6 |
28,7 |
12 |
6,3 |
15,8 |
13 |
6,9 |
15,1 |
14 |
7,1 |
20,1 |
15 |
8,5 |
13,3 |
16 |
8,7 |
14,7 |
Решение.
С помощью функции РЕГРЕССИЯ построим уравнение регрессии.
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика |
|
|
|
|
|
|
|
|
|
Множественный R |
0,846899 |
|
|
|
|
|
|
|
|
R-квадрат |
0,717238 |
|
|
|
|
|
|
|
|
Нормированный R-квадрат |
0,697041 |
|
|
|
|
|
|
|
|
Стандартная ошибка |
5,175943 |
|
|
|
|
|
|
|
|
Наблюдения |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
|
Регрессия |
1 |
951,3689 |
951,3689 |
35,51157 |
3,49E-05 |
|
|
|
|
Остаток |
14 |
375,0655 |
26,79039 |
|
|
|
|
|
|
Итого |
15 |
1326,434 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
|
Y-пересечение |
36,73164 |
3,528648 |
10,40955 |
5,67E-08 |
29,16344 |
44,29984 |
29,16344 |
44,29984 |
|
х |
-2,51209 |
0,421551 |
-5,95916 |
3,49E-05 |
-3,41623 |
-1,60795 |
-3,41623 |
-1,60795 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД ОСТАТКА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение |
Предсказанное у |
Остатки |
|
|
|
|
|
|
|
1 |
27,93933 |
6,160669 |
|
|
|
|
|
|
|
2 |
26,43208 |
2,867922 |
|
|
|
|
|
|
|
3 |
17,63977 |
-6,13977 |
|
|
|
|
|
|
|
4 |
23,66878 |
3,93122 |
|
|
|
|
|
|
|
5 |
24,42241 |
2,577593 |
|
|
|
|
|
|
|
6 |
4,828113 |
4,071887 |
|
|
|
|
|
|
|
7 |
-0,69848 |
9,298483 |
|
|
|
|
|
|
|
8 |
9,852291 |
-3,05229 |
|
|
|
|
|
|
|
9 |
12,8668 |
-8,8668 |
|
|
|
|
|
|
|
10 |
13,11801 |
-3,91801 |
|
|
|
|
|
|
|
11 |
25,17603 |
3,523966 |
|
|
|
|
|
|
|
12 |
20,90548 |
-5,10548 |
|
|
|
|
|
|
|
13 |
19,39823 |
-4,29823 |
|
|
|
|
|
|
|
14 |
18,89581 |
1,204189 |
|
|
|
|
|
|
|
15 |
15,37889 |
-2,07889 |
|
|
|
|
|
|
|
16 |
14,87647 |
-0,17647 |
|
|
|
|
|
|
|
Согласно полученным результатам уравнение регрессии
У(1)= 36,73-2,51Х, R²=0.717 R= 0.847
tст (10,409) (-5,95) F=35,51
Для оценки значимости параметров регрессии и модели в целом определим tкрит Fкрит и сравним их с расчетными величинами.
F(крит.)=4,6 (при a=0,05 и числе степеней свободы n1= k=1 и n2 = 16-2=14)
Так как F(набл)> F(крит), то модель значима
. По таблице t-распределения Стьюдента определяем tкр - критическое значение t-статистики для анализируемого уравнения
tкр (a=0,05; ν=n-2=16-2=14) =2.1448
так как Так как 10,409>2,1314 |-5,95|>2,1314, то значимыми являются коэффициенты а1 и а2
Проверим выполнение одной из предпосылок метода наименьших квадратов –постоянство дисперсий остатков уравнения регрессии.График остатков показывает, что остатки являются гомоскедатичными.
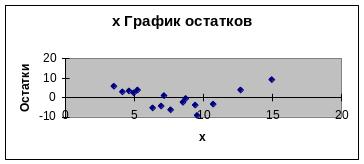
Проверим это предположение с помощью критерия Голдфелда-Квандта.
Проведем сортировку данных по х
х |
у |
3,5 |
34,1 |
4,1 |
29,3 |
4,6 |
28,7 |
4,9 |
27 |
5,2 |
27,6 |
6,3 |
15,8 |
6,9 |
15,1 |
7,1 |
20,1 |
7,6 |
11,5 |
8,5 |
13,3 |
8,7 |
14,7 |
9,4 |
9,2 |
9,5 |
4 |
10,7 |
6,8 |
12,7 |
8,9 |
14,9 |
8,6 |
Первая группа наблюдений (х от 3,5 до 6,3- 6 наблюдений)
Вторая группа наблюдений (х от 8,7 до 14,9-6 наблюдений)
Регрессия первой группы
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика |
|
|
|
|
|
|
|
|
Множественный R |
0,948591 |
|
|
|
|
|
|
|
R-квадрат |
0,899825 |
|
|
|
|
|
|
|
Нормированный R-квадрат |
0,874781 |
|
|
|
|
|
|
|
Стандартная ошибка |
2,148666 |
|
|
|
|
|
|
|
Наблюдения |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
Регрессия |
1 |
165,8813 |
165,8813 |
35,93019 |
0,003896 |
|
|
|
Остаток |
4 |
18,46706 |
4,616766 |
|
|
|
|
|
Итого |
5 |
184,3483 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
Y-пересечение |
55,60446 |
4,838319 |
11,49252 |
0,000327 |
42,17113 |
69,03779 |
42,17113 |
69,03779 |
х |
-5,98345 |
0,998211 |
-5,99418 |
0,003896 |
-8,75493 |
-3,21198 |
-8,75493 |
-3,21198 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессия второй группы наблюдений
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика |
|
|
|
|
|
|
|
|
Множественный R |
0,167863 |
|
|
|
|
|
|
|
R-квадрат |
0,028178 |
|
|
|
|
|
|
|
Нормированный R-квадрат |
-0,21478 |
|
|
|
|
|
|
|
Стандартная ошибка |
3,881139 |
|
|
|
|
|
|
|
Наблюдения |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Значимость F |
|
|
|
Регрессия |
1 |
1,747042 |
1,747042 |
0,11598 |
0,75057 |
|
|
|
Остаток |
4 |
60,25296 |
15,06324 |
|
|
|
|
|
Итого |
5 |
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
Y-пересечение |
11,42949 |
8,169863 |
1,398982 |
0,234382 |
-11,2537 |
34,11267 |
-11,2537 |
34,11267 |
Переменная X 1 |
-0,24851 |
0,729719 |
-0,34056 |
0,75057 |
-2,27454 |
1,777512 |
-2,27454 |
1,777512 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим отношение большей остаточной суммы квадратов к меньшей
Fрасч=SS3/SS1=60,25296/18,46706=3,26
Определим Fкрит (α=0,05, 1=6-1-1=4 =6-1-1=4), Fкрит=6,39
Так как Fкрит> Fрасч, то остатки регрессии являются гомоскедатичными.
Уравнение регрессии построенной по исходным данным является адекватным, имеет хорошее качество, его можно использовать для прогонозирования. Сделаем прогноз затрат на производство, если объем выпуска будет составлять 120% от среднего уровня. Хср=7,7875, Х(прогн)=1,2*7,7875=9,345 тыс.ед.
У(1)= 36,73-2,52*9,345=13,18 млн.ден.ед
Вывод. Уравнение регрессии У(1)= 36,73-2,52*Х, данное уравнение является адекватным, имеет хорошее качество. Прогноз затрат на производство, если объем выпуска будет составлять 120% от среднего уровня, т.е.9,345 тыс.ед- 13,18 млн.ден.ед.
