Коефіцієнти трудових витрат.

Модель Леонтьєва дає можливість дослідити і деякі проблеми стосовно використання і раціонального розподілу трудових ресурсів , що в свою чергу в значній мірі визначає ефективність економіки.

Маючи на меті доповнення моделі Леонтьєва введемо до розгляду вектор витрат трудових ресурсів l = (l₁, l₂, … , l_n) , де числа l_j > 0 (коефіцієнт трудових витрат) показує витрати трудових ресурсів в j-ій галузі при функціонуванні її технологічного процесу з одиничною інтенсивністю. Одиницею вимірювання l_j можуть бути як людино – дні чи людино – години, так і число працюючих. Технологія такої модифікованої моделі Леонтьєва задається парою ( l, А ).

Якщо загальний об’єм трудових ресурсів позначити через L, L > 0, то природно задати до моделі Леонтьєва обмеження на затрат трудових ресурсів

( х, l ) <= L , х >= 0 .

Тепер модифікована модель Леонтьєва запишеться так:

х – Ах = с, ( х, l ) <= L, x >= 0 (1)

Питання про існування розв’язку при довільному с >= 0 треба вивчати.

Нехай с >= 0 задає структуру кінцевого попиту. Пронормуємо його і наприклад, умовно || c || = 1. Запишемо задачу оптимізації:

(2)

Можна вважати, що мова йде про намір максимізувати кількість векторів – комплектів с . На меті ми маємо раціональний розподіл трудових ресурсів.

Твердження. Якщо матриця А продуктивна , то задача (2) допустима і має розв’язок.

▼Справді, оскільки А продуктивна то, поклавши x – Аx = с можна розв’язати

Виберемо число так, щоб і

Таке існує, бо L > 0 і, отже вектор є допустимим для задачі (2). Множина всіх допустимих векторів компактна, тому задача (2) має розвязок.

▲

Запишемо двоїсту задачу до (2) :

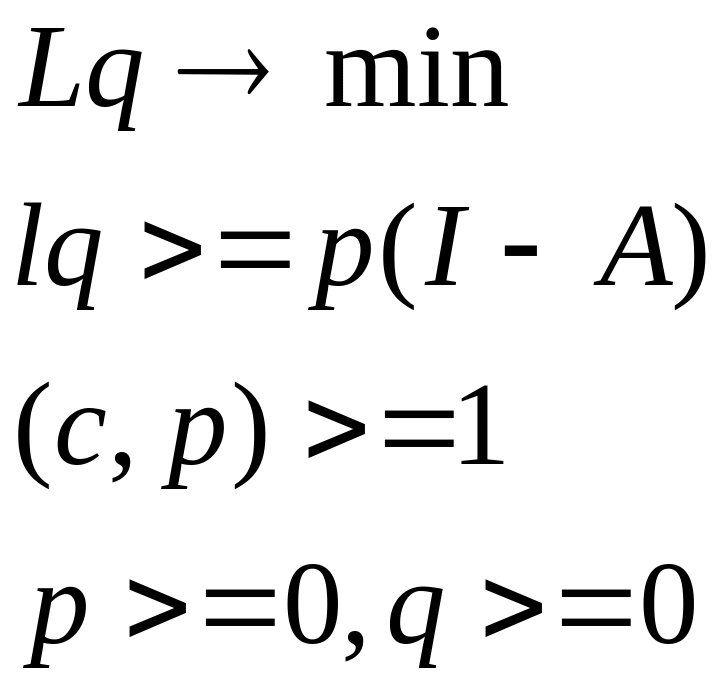(3)

p = (p₁, p₂, … , p_n) – вектор об’єктивно – зумовлених оцінок трудових витрат, q – число.

Покладемо l_q = p( I – A ) ( cp ) = 1. Тоді p = ql( I – A )^-1 і

x = ( I – А )^-1с , а для вектора трудових затрат маємо ( х, l ) = l ( I – A )^-1c.

Отже вектор l^* = l( I – A )^-1 буде вектором повних трудових витрат, j-а координата якого описує повні трудові витрати j-ї галузі економіки.

Можна інтерпретувати вектор p як вектор цін на продукти, а число q як ставку зарплати (зарплата на людино-день чи годину чи одного працівника). Тоді задача (3) зводиться до визначення p і q так, щоб мінімізувати загальний фонд зарплати Lq за умови p_j – (a^j, p) <= 0 j = 1,2, … n (чистий прибуток будь – якої галузі не є додатним)

Згідно теорії двоїстості

(4)

Оскільки (с, p) = 1, то є не що інше як загальна вартість товарів с при векторі цін p. Отже (4) : загальна вартість виробленого об’єму продукції дорівнює загальній сумі грошей які отримали всі учасники виробничого процесу як зарплату.

Розглянемо ще один варіант модифікації моделі Леонтьєва, який дозволяє виділити в задачі “споживчу” компоненту.

Будемо розглядати вектор с з як пайок, що йде на оплату праці одного працівника. Якщо x – вектор валового випуску (або вектор інтенсивностей), то матеріальні затрати на виробництво складуть величину Ax + Lc, де L– загальна кількість найманих працівників.

Враховуючи ресурсні обмеження(як матеріальних, так і трудових затрат) запишемо систему

Ax + Lc ≤ x

(l,x) ≤ L (5)

x ≥ 0

Питання існування розв’язку цієї системи вимагає спеціального дослідження. Нормуємо вектор x і введемо нову змінну y = x/l–валовий випуск в розрахунку на 1 працюючого. В нових змінних будемо мати:

Ay + C ≤ y

(l,y) ≤ 1 (6)

y ≥0

Означення: Модель виробництва з врахуванням споживання (5) є

c-продуктивною, якщо система нерівностей (6) є сумісна, тобто має розв’язок.

По суті c-продуктивність означає можливість оплатити працю кожного працівника, тобто можливість видати йому “пайок” в розмірі заданого вектора c.

Теорема Для c-продуктивності моделі (5) з невід’ємною нерозкладною технологічною матрицею A необхідно і достатньо щоб виконувалась нерівність:

l (I-A)^-1c ≤ 1 (7)

▼Якщо модель (5) є c-продуктивною, то число Фробеніуса _A < 1 і матриця (I-A)^-1 існує. Тому з першої нерівності (6) знайдемо:

y = (I-A)^-1 c ,

а друга нерівність з (6) приводить до (7).

Навпаки, якщо (7) виконана, то

х = (I-A)^-1c ≥ 0

є розв’язком системи (6), тобто модель (5) є c-продуктивна.

▲