Решение задачи с помощью программных систем
Решение задачи на lindo
LINDO – система для решения задач линейного, квадратичного и целочисленного программирования, разработанная для широкого круга пользователей.
Для решения задачи создаем файл с расширением .dat и вводим целевую функцию, перед этим определив, что нам требуется ее минимизировать, ограничения задачи, а также тип и количество переменных. В данном случае переменные целочисленные, поэтому указываем тип GIN. Чтобы получить решение, вводим команду GO. Далее в программе LINDO вводим команду TAKE <имя файла>,и на экран выводится решение задачи.
Входные данные
Входными данными для LINDO являются целевая функция, ограничения, тип и количество переменных. В приложении находится текст файла, при открытии которого выполняются вычисления.
Результаты вычислений
На рисунке 1 (а, б) приведены вычисленные значения управляемых переменных задачи. На рисунке 2 (а, б, в) показаны результаты вычисления ограничений.
a)
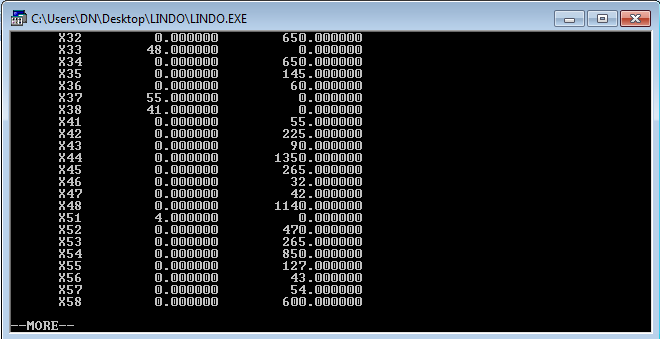
б)
Рисунок 1. Вычисление управляемых переменных
а)
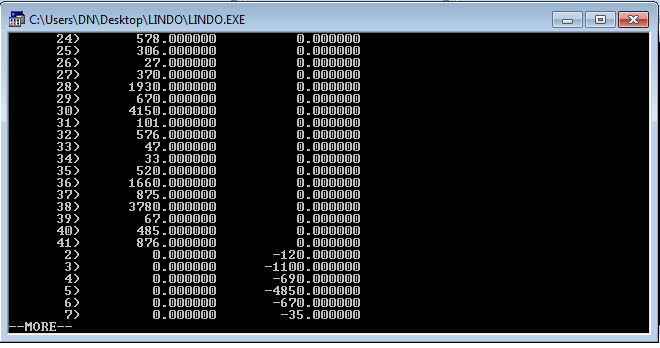
б)
в)
Рисунок 2. Вычисление ограничений
Таким образом, имеем следующее решение: значение целевой функции 247695, x12=53, x15=16, x16=28, x21=17, x24=11, x33=48, x37=55, x38=41, x51=4, остальные переменные равны 0.
Решение задачи на Excel
В системе электронных таблиц Microsoft Excel предусмотрен сервис «Поиск решения», с помощью которого можно автоматизировать решение задач оптимизации.
При решении задачи выбираются ячейки для хранения входных данных (ограничений, управляемых переменных), а также отдельная ячейка, в которой будет получено значение целевой функции.
Входные данные
Входными данными для Excel являются таблицы, в которые заносятся коэффициенты целевой функции, ограничения и формула целевой функции в отдельной ячейке.
Рисунок 3. Ввод коэффициентов целевой функции
Рисунок 4. Ввод формулы для расчета целевой функции
Рисунок 5. Ввод ограничений на потребность в ремонте
а)
б)
Рисунок 6. Ввод ограничений для допустимой загрузки баз
Результаты вычислений
Выбираем в меню Сервис «Поиск решения» и в появившемся окне (Рисунок 3) вводим сведения о местоположении ячейки для ЦФ, а также заполняем поле данных и ограничений, в т.ч. указываем ограничение целочисленности.
Рисунок 7. Окно сервиса «Поиск решений»
Далее нажимаем кнопку «Найти решение» и в пустых ячейках, отведенных под значения ЦФ и управляемых переменных, получаем решение. На рисунке 4 приведены вычисленные значения целевой функции и управляемых переменных.
Рисунок 8. Результаты вычислений
В итоге видим, что решение: значение целевой функции 247695, x12=53, x15=16, x16=28, x21=17, x24=11, x33=48, x37=55, x38=41, x51=4, остальные переменные равны 0 – полностью совпадет с решением, полученным в среде LINDO. Значит, задача решена правильно.
Экономический вывод и содержательная трактовка полученного результата
В ходе решения задачи был получен следующий план организации ремонта локомотивов:
На 1 ремонтной базе должно быть выполнено:
53 ремонта 3-го типа;
16 ремонтов 5-го типа;
28 ремонтов 6-го типа.
На 2 ремонтной базе должно быть выполнено:
17 ремонтов 1-го типа;
11 ремонтов 4-го типа.
На 3 ремонтной базе должно быть выполнено:
48 ремонтов 3-го типа;
55 ремонтов 7-го типа;
41 ремонт 8-го типа.
На 4 ремонтной базе ремонт локомотивов не выполняется.
На 5 ремонтной базе должно быть выполнено:
4 ремонта 1-го типа.
На выполнение ремонтов требуется выделить 247695 рублей, что соответствует минимальной возможной стоимости ремонта.
Таким образом, анализируя полученное решение, видим, что на ремонтной базе 4 ремонтов локомотивов не выполняется. Это связано с большими значениями стоимостей для данной базы, что значительно увеличивает величину целевой функции. Следовательно, исключаем данную базу из оптимального плана ремонта локомотивов.