2. Подъем, подача:

Чтобы определить, является ли значение ряда равновероятными, необходимо расположить их в возрастающей последовательности:

1,5 1,5 1,8 2 2,4 3,0

Далее определяется коэффициент разбросанности значений ряда:

В данном случае проверка хронометражного ряда выполняется по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда с предельно допустимыми значениями и решение вопроса о сокращении производственных значений в ряду.

Т.к. , то следует исключить

Получаем ряд:

1,5 1,5 1,8 2 2,4

Рассчитываем аналогично по методу определения предельных значений ряда.

Т.к. , то следует исключить

Получаем ряд:

1,5 1,5 1,8 2

В случае если можно считать, что все значения ряда равновероятны и, следовательно, на их основе может быть рассчитана средняя арифметическая величина затрат труда.

мин.

3. Устройство постели:

Чтобы определить, являются ли значения ряда равновероятными, необходимо расположить их в возрастающей последовательности:

1,6 1,8 2,5 2,5 2,5 3 4

Далее определяется коэффициент разбросанности значений ряда:

В данном случае, проверка хронометражного ряда выполняется по методу нахождения относительной средней квадратичной ошибки. В соответствии с ним улучшению подлежит такой ряд, в котором относительная величина средней квадратичной ошибки ( ) превышает установленное допустимое ее значение для данного ряда, т.е.если , где - допустимая относительная величина средней квадратичной ошибки в процентах. При числе элементов процесса до 5-ти ее значение составляет 7%, а свыше 5-ти 10%.

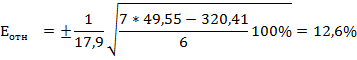
[ ]=10% для данного ряда, т.к. число элементов в нем свыше пяти.

12,6%>10% значит ряд подлежит улучшению.

В целях определения, какое из крайних значений ряда необходимо исключить, следует подсчитать два коэффициента и .

Если то исключить следует наибольшее значение ( ).

Получаем ряд:

1,6 1,8 2,5 2,5 2,5 3

В данном случае проверка хронометражного ряда выполняется по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда с предельно допустимыми значениями и решение вопроса о сокращении производственных значений в ряду.

Т.к. и удовлетворяют условиям, можно считать что все значения ряда равновероятны и, следовательно, на их основе может быть рассчитана средняя арифметическая величина затрат труда.

мин.

4. Установка:

Чтобы определить, являются ли значения ряда равновероятными, необходимо расположить их в возрастающей последовательности:

3 4 4,8 5 5 5 5

Далее определяется коэффициент разбросанности значений ряда:

В данном случае проверка хронометражного ряда выполняется по методу определения предельных значений ряда. Суть метода заключается в сопоставлении крайних значений упорядоченного исследуемого ряда с предельно допустимыми значениями и решение вопроса о сокращении производственных значений в ряду.

Т.к. , то следует исключить .

Получаем ряд:

4 4,8 5 5 5 5

В случае если можно считать, что все значения ряда равновероятны и, следовательно, на их основе может быть рассчитана средняя арифметическая величина затрат труда.

мин.