Формат числа одинарной точности

±	Порядок									Мантисса
1	8									23

Под порядок выделено 8 бит, поэтому смещение: .

Формат двойной точности

±	Порядок												Мантисса
1	11												52

Под порядок выделено 11 бит, поэтому смещение: .

Алгоритм получения числа с плавающей точкой

1. Перевести число из K-ичной системы счисления в двоичную (прямой код);

2. Представить двоичной число в нормализованной форме: ;

3. Рассчитать смещенный порядок числа: , где – смещение, зависящее от формата хранения;

4. Разместить знак, порядок и мантиссу в соответствующие разряды сетки;

5. Разбить полученное число на тетрады и записать полученные двоичные разряды в виде числа в 16-ичной системе.

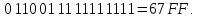
Алгоритм восстановления десятичного числа

1. Расписать по знакам исходное 16-ричное число на двоичные разряды;

2. По первому биту определить знак числа;

3. Вычислить истинный порядок: из смещенного порядка вычесть сдвиг порядка;

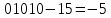
4. Записать знак, подразумеваемую единицу, в дробную часть выписать мантиссу, умножить полученное число на , упростить полученное выражение;

5. Перевести полученное число в десятичную систему счисления.

Характеристики некоторых форматов стандарта

Характеристика форматов	Одинарная точность	Двойная точность
Количество битов в знаке	1	1
Количество битов в экспоненте (порядке)	8	11
Количество битов в мантиссе	23	52
Общее число битов	32	64
Смещение экспоненты	127	1023
Область значений экспоненты	От -126 до 127	От -1022 до 1023
Самое маленькое нормализованное число	2-126	2-1022
Самое большое нормализованное число	2128	21024
Диапазон десятичных дробей	От 10-38 до 1038	От 10-308 до 10308
Самое маленькое ненормализованное число	10-45	10324
Название типа в C/C++	Float	Double